E N S
Durée : 4 heures
Les deux problèmes doivent être traités.
PREMIER PROBLÈME: OPTIQUE
Étude d'un spectroscope à prisme; application à une mesure interférentielle d'indice
I. On considère un prisme d'angle A et d'indice n (fig. 1).
I.1. En respectant les notations de la figure 1 et le choix du sens positif pour les angles, justifier rapidement les « formules » du prisme:
sin i = n sin r;
sin i' = n sin r';
A = r - r'.
I.2. Calculer la déviation D, du rayon émergent par rapport au rayon incident, en fonction de i ', i et A.
II. On considère le train de trois prismes disposés comme cela est indiqué sur la figure 2. Les deux prismes extrêmes sont identiques d'angle A = 90° et d'indice n. Le prisme intermédiaire a un angle A0 et un indice n0 . L'ensemble présente une symétrie par rapport au plan π bissecteur du dièdre A0 .
Les indices n et n0 sont fonctions de la longueur d'onde et leurs valeurs sont données dans le tableau I pour cinq longueurs d'onde:
TABLEAU 1
II. 1. Calculer la déviation D en fonction de i ', i et A0 .
II. 2. On veut que cette déviation soit nulle, pour la longueur d'onde λ0 = 589,3 nm, pour les rayons incidents parallèles à l'axe z'z orthogonal au plan π.
a. Tracer la marche d'un tel rayon.
b. Calculer A0 en fonction de n et n0, pour qu'il en soit ainsi.
c. Valeur numérique de A0 ?
III. On place un tel prisme dans le montage représenté sur la figure 3.
L1 et L2 sont deux objectifs identiques de focale f’1 = 200 mm, d'axes optiques confondus et paralléles à z'z. On dispose une fente très fine, perpendiculaire au plan de la figure 3 et passant par F, foyer objet de Ll; cette fente est éclairée par une source monochromatique de longueur d'onde λ0 = 589,3 nm. Les dimensions limitées du prisme font que l'onde plane émergente a une largeur a.
III. 1. a. Exprimer l'éclairement E (x') suivant l'axe F'x' de la tache de diffraction obtenue (F' est le foyer image de L1) en fonction de E(0) en F.
b. Calculer la largeur d0 du maximum central (distance entre les deux premiers zéros de E(x') de part et d'autre de x' = 0).
c. Application numérique: a = 20 mm.
III. 2. En réalité la fente F a une largeur l = 0,05 mm.
Quel est, dans ces conditions, l'aspect de l'éclairement sur l'axe F' x' ?
III. 3. On utilise maintenant, pour éclairer la fente F supposée très fine, une lampe à vapeurs métalliques qui émet un ensemble de raies monochromatiques dont les longueurs d'onde sont données dans le tableau I.
a. Calculer les positions x'λi des images de la fente F pour ces différentes longueurs d'onde.
b. Représenter la caractéristique (x'λi , λi ).
Dans cette représentation, on prendra 1 cm pour 1 mm en abscisse et 1 cm pour 10 nm en ordonnées, l'origine correspondant à x = 0, λ = λ0 = 589,3 nm.
IV. On éclaire maintenant le spectroscope défini précédemment par le montage des fentes d'Young représenté sur la figure 4.
L0 et L’0 sont deux lentilles identiques, dont les axes optiques coïncident, de focales f’0 = 200 mm.
La fente F0 est placée au foyer de L0 et le plan focal image de L0 coïncide avec le plan focal objet de L1; le conjugué de F0 coïncide avec la fente d'entrée F du spectroscope. Les fentes F1 et F2 ont une largeur l0 = 0,05 mm et sont distantes de s = 0,5 mm.
IV. 1. a. F0 étant éclairée par la source monochromatique de longueur d'onde λ0 = 589,3 nm, exprimer l'éclairement sur l'axe Fx, en supposant la fente placée en F0 très fine.
b. Montrer qu'une largeur de cette fente égale à 0,05 mm est compatible avec l'obtention de franges de bon contraste.
c. Quel est l'aspect de l'éclairement de F'x' dans le spectroscope ?
IV. 2. On dispose devant la fente F1 des fentes d'Young une lame de verre d'épaisseur e = 0,018 mm et d'indice n' (indice que l'on supposera, par la suite, indépendant de la longueur d'onde).
a. Calculer le nouvel éclairement sur Fx, F0 étant toujours éclairé par la source de longueur d'onde λ0.
b. L'éclairement obervé dans le spectroscope sur F'x' est nul; que peut-on en conclure ?
c. On éclaire maintenant F0 par une source de lumière blanche (distribution continue d'énergie sur tout le spectre visible de 400 nm à 800 nm). Qu'observe-t-on dans le spectroscope sur F'x' en l'absence de lame sur F1?
d. En présence de la lame devant F1 on voit apparaître sur F'x' des zones d'éclairement nul (cannelures):
DEUXIEME PROBLEME: ELECTRICITELes deux problèmes doivent être traités.
PREMIER PROBLÈME: OPTIQUE
Étude d'un spectroscope à prisme; application à une mesure interférentielle d'indice
I. On considère un prisme d'angle A et d'indice n (fig. 1).
I.1. En respectant les notations de la figure 1 et le choix du sens positif pour les angles, justifier rapidement les « formules » du prisme:
sin i = n sin r;
sin i' = n sin r';
A = r - r'.
I.2. Calculer la déviation D, du rayon émergent par rapport au rayon incident, en fonction de i ', i et A.
Les indices n et n0 sont fonctions de la longueur d'onde et leurs valeurs sont données dans le tableau I pour cinq longueurs d'onde:
TABLEAU 1
| λ (nm) | 706,5 | 643,8 | 589,3 | 546,1 | 486,1 |
| n | 1,50707 | 1,50895 | 1,51105 | 1,51314 | 1,51700 |
| n0 | 1,62818 | 1,63191 | 1,63620 | 1,6402 | 1,64909 |
II. 2. On veut que cette déviation soit nulle, pour la longueur d'onde λ0 = 589,3 nm, pour les rayons incidents parallèles à l'axe z'z orthogonal au plan π.
a. Tracer la marche d'un tel rayon.
b. Calculer A0 en fonction de n et n0, pour qu'il en soit ainsi.
c. Valeur numérique de A0 ?
III. On place un tel prisme dans le montage représenté sur la figure 3.
L1 et L2 sont deux objectifs identiques de focale f’1 = 200 mm, d'axes optiques confondus et paralléles à z'z. On dispose une fente très fine, perpendiculaire au plan de la figure 3 et passant par F, foyer objet de Ll; cette fente est éclairée par une source monochromatique de longueur d'onde λ0 = 589,3 nm. Les dimensions limitées du prisme font que l'onde plane émergente a une largeur a.
b. Calculer la largeur d0 du maximum central (distance entre les deux premiers zéros de E(x') de part et d'autre de x' = 0).
c. Application numérique: a = 20 mm.
III. 2. En réalité la fente F a une largeur l = 0,05 mm.
Quel est, dans ces conditions, l'aspect de l'éclairement sur l'axe F' x' ?
III. 3. On utilise maintenant, pour éclairer la fente F supposée très fine, une lampe à vapeurs métalliques qui émet un ensemble de raies monochromatiques dont les longueurs d'onde sont données dans le tableau I.
a. Calculer les positions x'λi des images de la fente F pour ces différentes longueurs d'onde.
b. Représenter la caractéristique (x'λi , λi ).
Dans cette représentation, on prendra 1 cm pour 1 mm en abscisse et 1 cm pour 10 nm en ordonnées, l'origine correspondant à x = 0, λ = λ0 = 589,3 nm.
IV. On éclaire maintenant le spectroscope défini précédemment par le montage des fentes d'Young représenté sur la figure 4.
L0 et L’0 sont deux lentilles identiques, dont les axes optiques coïncident, de focales f’0 = 200 mm.
La fente F0 est placée au foyer de L0 et le plan focal image de L0 coïncide avec le plan focal objet de L1; le conjugué de F0 coïncide avec la fente d'entrée F du spectroscope. Les fentes F1 et F2 ont une largeur l0 = 0,05 mm et sont distantes de s = 0,5 mm.
IV. 1. a. F0 étant éclairée par la source monochromatique de longueur d'onde λ0 = 589,3 nm, exprimer l'éclairement sur l'axe Fx, en supposant la fente placée en F0 très fine.
b. Montrer qu'une largeur de cette fente égale à 0,05 mm est compatible avec l'obtention de franges de bon contraste.
c. Quel est l'aspect de l'éclairement de F'x' dans le spectroscope ?
a. Calculer le nouvel éclairement sur Fx, F0 étant toujours éclairé par la source de longueur d'onde λ0.
b. L'éclairement obervé dans le spectroscope sur F'x' est nul; que peut-on en conclure ?
c. On éclaire maintenant F0 par une source de lumière blanche (distribution continue d'énergie sur tout le spectre visible de 400 nm à 800 nm). Qu'observe-t-on dans le spectroscope sur F'x' en l'absence de lame sur F1?
d. En présence de la lame devant F1 on voit apparaître sur F'x' des zones d'éclairement nul (cannelures):
- établir les relations qui existent entre e, n' - 1 et les longueurs d'onde correspondant aux cannelures;
- en particulier, on note une cannelure en x’1 = - 5,6 mm et une cannelure en x’2 = 3,4 mm et p = 3 cannelures entre ces deux cannelures. En déduire la valeur de l'indice n' .
Aspects énergétiques des dipôles
(Cf figures en fin de problème)
Dans tout le problème, on ne considère que des états de régimes forcés de tensions et de courants. Au cours de la question 4., il est fait usage de la puissance réactive, il n'est pas nécessaire de connaître les propriétés de cette grandeur pour résoudre le problème: la seule définition donnée au cours de cette question suffit pour la résolution.
2. La tension v ( t) est sinusoïdale et de la forme:
v = V $\sqrt 2 \;\;\sin \;(\omega t\; + \;\varphi \;)$
où V = 231 volts, la fréquence est 50 Hz et ( ϕ désigne un angle compris dans l'intervalle $\left( { - \;\;\frac{\pi }{2}\;\;,\;\; + \;\;\frac{\pi }{2}} \right)$.
Le courant est alors i (t) = $\sqrt 2 \;\;\sin \;\omega t\;$. Préciser p (t) et établir l'expression en fonction de V, I, ϕ de la puissance active de ce dipôle (valeur moyenne de p ( t) que l'on notera P).
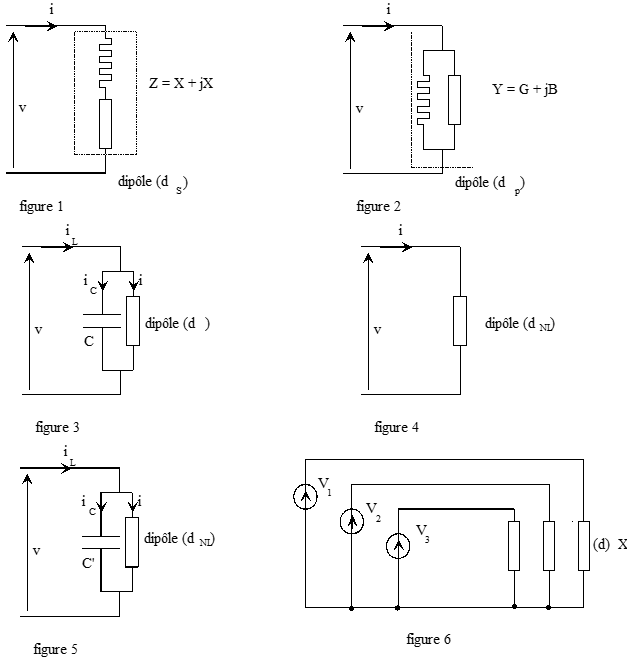
3. Un dipôle série (dS) est constitué par la mise en série d'une résistance R et d'une réactance (positive ou négative) que l'on note X (cf. fig. 1). Exprimer P en fonction de R et I.
4. On définit une grandeur Q (unité: VAR) appelée puissance réactive par la relation:
Q = $\frac{1}{T}\;\;\int_0^T {{v_q}\;i\;dt} $ où vq = V $\sqrt 2 \;\;\sin \;(\omega t\; + \;\varphi \; - \;\frac{\pi }{2})$
Établir l'expression de Q en fonction de V, I, ϕ, puis en fonction de X et I.
5. On considère à présent un dipôle (dp) constitué par la mise en parallèle de deux éléments dont l'un est purement résistif (cf. fig. 2). L'admlttance complexe totale est notée par: Y = G + jB. La tension instantanée v (t) et le courant i (t) sont toujours donnés par les expressions:
v = V $\sqrt 2 \;\;\sin \;(\omega t\; + \;\varphi \;)$ et i (t) = $\sqrt 2 \;\;\sin \;\omega t\;$.
Quelle relation existe-t-il entre ϕ, G et B ? Déterminer l'expression de P en fonction de G et V et celle de Q en fonction de B et V.
6. On définit l'équivalence énergétique de deux dipôles de la façon suivante: deux dipôles seront considérés comme énergétiquement équivalents s'ils absorbent les mêmes puissances actives et les mêmes puissances réactives lorsqu'ils sont soumis à une même tension sinusoïdale.
6.2. Un dipôle (dS) série, caractérisé par R et X, est énergétiquement équivalent à un dipôle parallèle (dp) caractérisé par G et B: exprimer G puis B en fonction de R et X. Quelle est la relation entre l'impédance complexe Z = R + jX et l'admittance complexe Y = G + jB qui en résulte ?
7. On a expérimentalement établi pour un dipôle (d) les valeurs numériques des grandeurs suivantes:
V = 231 V ; P = 3 465 W ; Q = 6 000 VAR.
Calculer les valeurs G et B du dipôle (dp) équivalent et celles R et X du dipôle série équivalent. Quel est le déphasage de la tension par rapport au courant ?
8. Caractériser G et B pour une inductance pure. Même question pour un condensateur de capacité C.
9. Le dipôle (d) de la question 7. est mis en parallèle avec un condensateur de capacité C (fig. 3). Tracer le diagramme de Fresnel des tensions et courants dans un cas général pour une valeur quelconque de C. Quelle doit être la relation entre C, G et B pour que le déphasage ϕ' entre la tension v et le courant total iL ait une valeur fixée ϕ'0 ?
Calculer C pour que ϕ'0 ait la valeur + 15° puis la valeur - 15°. Quelles sont les valeurs efficaces de iL qui en résultent ?
10. On considère à présent un dipôle non linéaire (dNL) (fig. 4), qui est caractérisable de la façon suivante: soumis à une tension sinusoïdale v = V $\sqrt 2 \;\;\sin \;(\omega t\; + \;\varphi \;)$ (V = 231 V; f = 50 Hz), il absorbe un courant non sinusoïdal développable en série de Fourier:
$i(t) = {I_1}\;\sqrt 2 \;\sin \omega t\;\; - \;\;{I_5}\;\sqrt 2 \;\sin \;5\omega t\;\; - \;{I_7}\;\sqrt 2 \;\sin \;7\omega t\;$
Pour la suite, on néglige les harmoniques d'ordre supérieur à 7.
10.1. Quelle est l'expression de p (t), quelle est sa période ? Tracer la loi de variation en fonction du temps pour les valeurs suivantes:
Il = 35 A ; I5 = 7 A ; I7 = 1 A et ϕ = 60° .
10.2 Quelles sont l'expression et la valeur numérique de la puissance moyenne P ?
10.3. Compte tenu de la définition de Q donnée à la question 4, déterminer Q et faire l'application numérique correspondante.
10.4. Calculer la valeur efficace du courant i.
10.5. On place un condensateur de capacité C' en parallèle sur le dipôle (dNL) conformément à la figure 5, déterminer la valeur de C' qui rend minimale la valeur efficace du courant iL.
11. La figure 6 représente la mise en parallèle de trois circuits du même type que ceux de la figure 1. Les trois tensions sont données par les expressions:
v1 = V $\sqrt 2 \;\;\sin \;(\omega t\; + \;\varphi \;)$ ; v2 = V $\sqrt 2 \;\;\sin \;(\omega t\; + \;\varphi \; + \;\theta )$ ; v3 = V $\sqrt 2 \;\;\sin \;(\omega t\; + \;\varphi \; + \;\psi )$.
Les trois dipôles (d) de la figure sont identiques et les courants il , i2, i3 qui circulent sont donnés par les expressions:
i1 = I $\sqrt 2 \;\;\sin \;\omega t\;$ ; i2 = I $\sqrt 2 \;\;\sin \;(\omega t\; + \;\theta )$ ; i3 = I $\sqrt 2 \;\;\sin \;(\omega t\; + \;\psi )$.
Dans ces expressions V = 231 V, I = 35 A, la fréquence est 50 Hz; (p - 30° et les angles θ et ψ sont à déterminer suivant certaines conditions. La puissance instantanée p est définie à partir des puissances instantanées p1, p2, p3 dans chaque dipôle récepteur par: p = p1 + p2 + p3.
11.1. Établir, en se servant des résultats des questions précédentes, l'expression de la puissance moyenne mise en jeu dans chaque dipôle (d). Application numérique.
p(t) = A + F(t)
où A est une constante et F ( t) une fonction du temps.
Préciser l'expression de F (t). Quelle(s) relation(s) doivent vérifier θ et ψ pour que F (t) soit nulle pour tout t ? Proposer des valeurs de θ et ψ satisfaisant à cette condition.





Aucun commentaire:
Enregistrer un commentaire