Concours Physique ENS Cachan 1995 (Corrigé)

Avertissement:
1) les graphes étant tous semblables (des exponentielles croissantes), il n’en a été tracé que l’allure;
2) dans la question 3.3.3-, mes applications numériques me conduisent toujours à un régime oscillant, qui n’est pas dans la logique de l’énoncé; j’ai donc renoncé au tracé demandé.

ENS Cachan B(A) 1995

Première partie: Étude électromagnétique
1.1- Spire équivalente:
1.1.1- La force de Laplace a pour expresion: ${\rm{d\vec f}} = {\rm{dI}}{\kern 1pt} {\rm{\vec u}} \wedge {\rm{\vec B}}$

1.1.2- On considère une spire élémentaire de section ldr, de longueur 2πr, parcourue par le courant d’intensité ${\rm{dI}} = \delta {\rm{ldr}}$, où $\delta =\frac{I}{\left[ l \left( R_e - R_i \right) \right]}$; elle est soumise à la force: ${\rm{\vec f}} = \int_{{{\rm{R}}_{\rm{i}}}}^{{\rm{Re}}} {\;\delta {\rm{ldr2}}\pi {\rm{rB}}{{{\rm{\vec e}}}_{\rm{z}}}} = \delta \frac{{\rm{L}}}{{\rm{N}}}\pi {\rm{B}}\left( {{{\rm{R}}_{\rm{e}}}^2 - {{\rm{R}}_{\rm{i}}}^2} \right){{\rm{\vec e}}_{\rm{z}}}$ 1.1.3- On constate en effet que l’on peut écrire: ${\rm{\vec f}} = {\rm{IB2}}\pi {\rm{R}}{{\rm{\vec e}}_{\rm{z}}}$

1.2- Force électromagnétique résultante:
1.2.1- Le résultat est immédiat: ${\rm{\vec F}} = {\rm{N\vec f}} = {\rm{NIB2}}\pi {\rm{R}}{{\rm{\vec e}}_{\rm{z}}}$
1.2.2- On peut écrire F sous la forme indiquée en posant: ${{\rm{k}}_\phi } = {\rm{B2}}\pi {\rm{R}}$
C’est homogène à une circulation du champ magnétique B, mais cela ne correspond pas à une circulation concrête.
1.2.3- AN: ${{\rm{I}}_{\rm{e}}} = \delta {\rm{L}}\left( {{{\rm{R}}_{\rm{e}}} - {{\rm{R}}_{\rm{i}}}} \right) = 800\;{\rm{A}}\,{\rm{;}}\quad {\rm{F}} = {\rm{78}}{\rm{,4}}\;{\rm{N}}$
1.3- Force contre électromotrice:
1.3.1- On sait que le champ électromoteur est: ${{\rm{\vec E}}_{\rm{M}}} = {\rm{\vec v}} \wedge {\rm{\vec B}} = {\rm{Bv}}{{\rm{\vec u}}_\theta }$ et la fem: ${\rm{e}} = \int {{{{\rm{\vec E}}}_{\rm{M}}}.{\rm{d\vec M}}} = {\rm{Bvu}}$
1.3.2- Il est clair que: ${\rm{e}} = {\rm{Bv2}}\pi {\rm{R}}\quad \Rightarrow \quad {{\rm{k}}^{\rm{'}}}_\phi = {\rm{B2}}\pi {\rm{R}} = {{\rm{k}}_\phi }$ AN: ${{\rm{e}}_{\rm{0}}} = {\rm{9}}{\rm{,80}}{\rm{.1}}{{\rm{0}}^{{\rm{ - 2}}}}\;{\rm{V}}$
1.3.3- Le résultat est immédiat: ${\rm{E}} = {\rm{Ne}}$
1.4- Calcul de la résistance:
1.4.1- La résistance se calcule par la formule:
${\rm{R}} = \rho \frac{{\rm{l}}}{{\rm{S}}}\quad \Rightarrow \quad {{\rm{R}}_{\rm{b}}} = \rho \frac{{{\rm{2}}\pi {\rm{R}}{{\rm{N}}^{\rm{2}}}}}{{{\rm{L}}\left( {{{\rm{R}}_{\rm{e}}} - {{\rm{R}}_{\rm{i}}}} \right)}}\quad \Rightarrow \quad$${{\rm{r}}_{\rm{b}}} = \rho \frac{{{\rm{2}}\pi {\rm{R}}}}{{{\rm{L}}\left( {{{\rm{R}}_{\rm{e}}} - {{\rm{R}}_{\rm{i}}}} \right)}}$
1.4.2- AN: ${{\rm{r}}_{\rm{b}}} = {\rm{1}}{\rm{,23}}{\rm{.1}}{{\rm{0}}^{{\rm{ - 4}}}}\;\Omega$
1.5- Calcul de l’inductance:

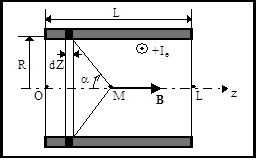
1.5.1.a- Tout plan contenant l’axe Oz est plan d’antisymétrie pour la distribution de courants; il s’ensuit que le champ magnétique${\rm{\vec B}}$ est dirigé selon l’axe Oz, la « règle du tire-bouchon » donnant alors le sens du vecteur. À partir de la loi de Biot & Savart, on retrouve le résultat: ${\rm{dB = }}\frac{{{\mu _{\rm{0}}}}}{{{\rm{2R}}}}\frac{{{{\rm{I}}_{\rm{e}}}{\rm{dZ}}}}{{\rm{L}}}{\rm{si}}{{\rm{n}}^{\rm{3}}}\left( \alpha \right)$ où Z est la position de la spire (z étant celle du point M).

1.5.1.b- Dans un premier temps, on a intérêt à intégrer selon la variable α:
${\rm{cot}}\left( \alpha \right) = \frac{{{\rm{z}} - {\rm{Z}}}}{{\rm{R}}}\quad \Rightarrow \quad {\rm{dZ}} = \frac{{{\rm{Rd}}\alpha }}{{{\rm{si}}{{\rm{n}}^{\rm{2}}}\left( \alpha \right)}}\quad \Rightarrow \quad {\rm{dB}} = \frac{{{\mu _0}{{\rm{I}}_{\rm{e}}}}}{{2{\rm{L}}}}{\rm{sin}}\left( \alpha \right){\rm{d}}\alpha \quad \Rightarrow \quad {\rm{B}} = \frac{{{\mu _{\rm{0}}}{{\rm{I}}_{\rm{e}}}}}{{{\rm{2L}}}}\left[ {{\rm{cos}}\left( {{\alpha _{\rm{1}}}} \right) - {\rm{cos}}\left( {{\alpha _{\rm{2}}}} \right)} \right]$
On en déduit: ${\rm{\vec B}}\left( {\rm{z}} \right) = \frac{{{\mu _{\rm{0}}}{{\rm{I}}_{\rm{e}}}}}{{{\rm{2L}}}}\left[ {\frac{{\rm{z}}}{{\sqrt {{{\rm{R}}^{\rm{2}}} + {{\rm{z}}^{\rm{2}}}} }} + \frac{{{\rm{L}} - {\rm{z}}}}{{\sqrt {{{\rm{R}}^{\rm{2}}} + {{\left( {{\rm{L}} - {\rm{z}}} \right)}^2}} }}} \right]{{\rm{\vec e}}_{\rm{z}}}$
1.5.1.c- On calcule la valeur du rapport demandé et l’on constate que B varie relativement peu sur l’axe, à l’intérieur de la spire.
$B \left( 0 \right) = \frac{\mu_{0} I_{e}}{2 \sqrt{R{2} + L^{2}}} \ ; \ B \left( \frac{L}{2} \right) = \frac{\mu _{0}I_{e}}{\sqrt {4R^{2} + L^{2}}} \Rightarrow  \frac{B \left( 0 \right)}{B \left( \frac{L}{2} \right)}= \frac{\sqrt {4R^{2} + L^{2}}}{2 \sqrt{R^{2} + L^{2}}} = 0,785$
1.5.2- Compte tenu des hypothèses simplificatrices, le calcul est aisé:
${{\text{W}}_{\text{mag}}}=\iiint{\frac{{{\text{B}}^{\text{2}}}}{\text{2}{{\mu }_{\text{0}}}}\,}\text{d}\tau =\frac{{{\text{B}}^{\text{2}}}}{\text{2}{{\mu }_{\text{0}}}}\pi {{\text{R}}^{\text{2}}}\text{L}\quad \Rightarrow \quad {{\rm{W}}_{{\rm{mag}}}} = \frac{{\pi {\mu _{\rm{0}}}{{\rm{R}}^{\rm{2}}}{\rm{L}}{{\rm{I}}_{\rm{e}}}^2}}{{{\rm{2}}\left( {{\rm{4}}{{\rm{R}}^{\rm{2}}} + {{\rm{L}}^{\rm{2}}}} \right)}}$
1.5.3- De la relation: ${{\text{W}}_{\text{mag}}}=\frac{1}{2}{{\text{I}}^{2}}$, on tire:
$=\frac{\pi {{\mu }_{0}}{{\text{R}}^{\text{2}}}\text{L}}{\text{4}{{\text{R}}^{\text{2}}}+{{\text{L}}^{\text{2}}}}\,{{\text{N}}^{\text{2}}}$ $=\frac{\pi {{\mu }_{0}}{{\text{R}}^{\text{2}}}\text{L}}{\text{4}{{\text{R}}^{\text{2}}}+{{\text{L}}^{\text{2}}}}={{1,56.10}^{-8}}\ H$

1.6- Équation différentielle: 1.6.1- On a affaire à un circuit série comportant un générateur de fem U, une force électromotrice E, une inductance propre L et une résistance Rb . L’équation différentielle du circuit est: $\text{U}=\text{E+}\frac{\text{dI}}{\text{dt}}+{{R}_{b}}I$ 1.6.2- En remplaçant les grandeurs par leurs expressions: $\text{U}=\text{N}\left( {{\text{k}}_{\phi }}v+\frac{d{{I}_{e}}}{dt}+{{r}_{b}}{{I}_{e}} \right)$

1.7- Détermination du nombre de spires:
1.7.1- Des deux équations: ${U_0} = {N_0}\left( {{k_\phi }{V_0} + {r_b}{I_e}} \right)$ et $F = {k_\phi }{I_e}$, on déduit: ${N_0} = \frac{U_0}{k_{\phi }V_{0} + r_{b}\frac{F}{k_{\phi}}}$
1.7.2- ${N_0}$ permet d’ajuster la valeur de $k_{\phi }V_{0} + r_{b}\frac{F}{k_\phi }$.
1.7.3- AN: ${N_0} = 61\;spires$ ${R_b} = 0,456\,\Omega$ $=58,2\,\mu H$ ${E_0} = 5,98\,V$
1.8- Échelon de tension:
1.8.1- cas a: solénoïde immobilisé; pour $t = 0$, la forme de l’équation différentielle imposant la continuité de l’intensité, elle s’intègre en:
$\frac{di}{dt}+{{R}_{b}}i={{U}_{0}}\quad \Rightarrow \quad$${{i}_{a}}\left( t \right)=\frac{{{U}_{0}}}{{{R}_{b}}}\left[ 1-\exp \left( -\frac{{{R}_{b}}}{}t \right) \right]$
1.8.1- cas b: solénoïde à vitesse uniforme; il suffit de changer ${U_0}$ en ${U_0} - {E_0}$, soit:
$\frac{di}{dt}+{{R}_{b}}i={{U}_{0}}-{{E}_{0}}\quad \Rightarrow \quad$${{i}_{b}}\left( t \right)=\frac{{{U}_{0}}-{{E}_{0}}}{{{R}_{b}}}\left[ 1-\exp \left( -\frac{{{R}_{b}}}{}t \right) \right]$

AN: ${i_a}{\left( t \right)_{\left[ A \right]}} = 27,2\exp \left( { - {{7,84.10}^3}t} \right)$ ${i_b}{\left( t \right)_{\left[ A \right]}} = 13,9\exp \left( { - {{7,84.10}^3}t} \right)$ Les exponentielles appartenant à la catégorie des « fonctions bien connues », seule l’allure des courbes a été tracée. 1.8.2- La constante de temps ne dépend pas du nombre de spires car elle vaut: ${{\tau }_{e}}=\frac{}{{{\text{R}}_{\text{b}}}}=\frac{{{\mu }_{0}}{{L}^{2}}\left( {{R}_{e}}-{{R}_{i}} \right)R}{2\rho \,\left( \text{4}{{\text{R}}^{\text{2}}}+{{\text{L}}^{\text{2}}} \right)}=128\,\mu s$

Deuxième partie: Étude thermique
2.1- Pertes Joule:
La puissance dissipée par effet Joule est égale à:
${P_J} = {R_b}{I^2} = \rho \frac{{{\rm{2}}\pi {\rm{R}}{{\rm{N}}^{\rm{2}}}}}{{{\rm{L}}\left( {{{\rm{R}}_{\rm{e}}} - {{\rm{R}}_{\rm{i}}}} \right)}}{\left[ {\delta \frac{L}{N}\left( {{{\rm{R}}_{\rm{e}}} - {{\rm{R}}_{\rm{i}}}} \right)} \right]^2}\quad \Rightarrow \quad$${P_J} = \pi \rho {\delta ^2}=L\left( {{R_e}^2 - {R_i}^2} \right) = 78,4\;W$
La densité volumique de puissance peut s’écrire directement, sans passer par ${P_J}$:
${p_J} = \rho {\delta ^2} = 32,0 \ MW/m^3$

2.2- Schéma équivalent:
2.2.1- Le schéma équivalent correspond à l’équation: ${P_J} = {C_{th}}\frac{{d\left( {\Delta \theta } \right)}}{{dt}} + \frac{{\Delta \theta }}{{{R_{th}}}}$.
La capacité thermique (et non calorifique) du solénoïde vaut: ${C_{th}} = c\varpi \pi \left( {{R_e}^2 - {R_i}^2} \right)$
Pour obtenir la résistance thermique d’échange, on exprime cet échange de deux façons:
$\frac{{\Delta \theta }}{{{R_{th}}}} = \alpha 2\pi {R_i}L\Delta \theta + \alpha 2\pi {R_e}L\Delta \theta \quad \Rightarrow \quad$${R_{th}} = \frac{1}{{\alpha 2\pi L\left( {{R_i} + {R_e}} \right)}}$
2.2.2- AN: ${C_{th}} = 425\;J.{K^{ - 1}}$ ${R_{th}} = 17,0\;K.{W^{ - 1}}$
2.2.3- Les échanges de chaleur se font par conduction, convexion et rayonnement.
2.3- Évolution de la température du solénoïde:

2.3.1- L’équation différentielle du 2.2.1- s’intègre comme celle du 1.8.1-: ${\theta _S} = {\theta _{amb}} + {P_J}{R_{th}}\left[ {1 - \exp \left( { - \frac{t}{{{R_{th}}{C_{th}}}}} \right)} \right]$ $\theta {}_S = 20 + 1333\left[ {1 - \exp \left( { - {{1,384.10}^{ - 4}}t} \right)} \right]$ À nouveau, seule l’allure du graphe est donnée. 2.3.2- La constante de temps vaut: ${\tau _{th}} = {R_{th}}{C_{th}} = 7,23\;ks$

2.3.3- Le calcul de la densité de courant est immédiat: ${P_J}{R_{th}} = 100\;K\quad \Rightarrow \quad$${\delta _P} = 11,0\;A.m{m^{ - 2}}$
2.3.4- La durée maximale est: ${t_{\max }} = - {\tau _{th}}\ln \left( {1 - \frac{{{\theta _{S\max }} - {\theta _{amb}}}}{{P{}_J{R_{th}}}}} \right) = 564\;s$
2.3.5.a- Physiquement, cela veut dire que la chaleur produite est restée dans la spire et n’a pas encore commencé à être évacuée vers l’extérieur; l’équation du 2.2.1- se résume à:
${P_J} \approx {C_{th}}\frac{{d\left( {\Delta \theta } \right)}}{{dt}}\quad \Rightarrow \quad$$\Delta \theta \left( t \right) \approx \frac{{{P_J}}}{{{C_{th}}}}t = \frac{{\rho L{\delta ^2}}}{{c\varpi }}t$ $\quad \Rightarrow \quad$$\Delta \theta \left( {{T_0}} \right) \approx 1,84\;^\circ C$
Mathématiquement, dans l’équation du 2.3.1-, on développe:$\exp \left( \varepsilon \right) \approx 1 + \varepsilon$.
2.3.5.b- On déduit de ce qui précède la densité maximale de courant: ${\delta _{\max }} \approx \sqrt {\frac{{c\varpi \left( {{\theta _{S\max }} - {\theta _{amb}}} \right)}}{{\rho L{T_0}}}}$
2.3.5.c- AN: ${\left( {{\delta _{\max }}} \right)_{Cu}} \approx 294\;A.m{m^{ - 2}}$ ${\left( {{\delta _{\max }}} \right)_{Al}} \approx 198\;A.m{m^{ - 2}}$
2.3.5.d- On calcule F à partir de la formule:
$F = \pi BL\delta \left( {{R_e}^2 - {R_i}^2} \right)$ $\quad \Rightarrow \quad$${F_{Cu}} = 576\;N$ $F{}_{Al} = 388\;N$
2.3.5.e- En régime permanent, ${P_J}{R_{th}} = \frac{\rho }{{2\alpha }}\left( {{R_e} - {R_i}} \right){\delta ^2} = \Delta \theta$, dont on déduit:
$\left\{ \begin{array}{l}{\delta _{Cu}} = 11,0\;A.m{m^{ - 2}}\; \Rightarrow \;{F_{Cu}} = 21,5\;N\\{\delta _{Al}} = 8,80\;A.m{m^{ - 2}}\; \Rightarrow \;{F_{Al}} = 17,2\;N\end{array} \right.$

Troisième partie: Étude électromécanique et thermique
3.1- Masse du solénoïde:
La masse du solénoïde est égale à: $M = \varpi \pi L\left( {{R_e}^2 - {R_i}^2} \right)\,;\quad {M_{Cu}} = 21,8\;g\,;\quad {M_{Al}} = 6,62\;g$

3.2- Solénoïde ouvert: L’équation différentielle $M\frac{{dv}}{{dt}} + \mu v = F$ s’intègre en: $v = \frac{{{F_0}}}{\mu }\left[ {1 - \exp \left( { - \frac{\mu }{M}t} \right)} \right]$ La constante de temps mécanique a pour valeur: ${\left( {{\tau _m}} \right)_{Cu}} = \frac{M}{\mu } = 0,218 \ s$

3.3- Solénoïde alimenté:
3.3.1- Les équations rappelées par l’énoncé sont les suivantes:
1.2.2-$\;{\rm{F = }}{{\rm{k}}_\phi }NI\;;$ 1.3.3- $E = N{k_\phi }v\;;$ 1.6.1- $U=E+\frac{dI}{dt}+{{R}_{b}}I$
Par élimination de I entre les équations: $M\frac{{dv}}{{dt}} + \mu v = {k_\phi }NI$, et: $U=N{{k}_{\phi }}v+\frac{dI}{dt}+{{R}_{b}}I$, on trouve:
$U=\frac{M}{{{k}_{\phi }}N}\frac{{{d}^{2}}v}{d{{t}^{2}}}+\frac{\mu +M{{R}_{b}}}{{{k}_{\phi }}N}\frac{dv}{dt}+\left( {{k}_{\phi }}N+\frac{{{R}_{b}}\mu }{{{k}_{\phi }}N} \right)v\ ;\ a=\frac{M}{{{k}_{\phi }}N}\ ;\ b=\frac{\mu +M{{R}_{b}}}{{{k}_{\phi }}N}\ ;\ c={{k}_{\phi }}N+\frac{{{R}_{b}}\mu }{{{k}_{\phi }}N}$
3.3.2- La première approximation: ${{\tau }_{e}}=\frac{}{{{R}_{b}}}<<{{\tau }_{m}}=\frac{M}{\mu }$ s’écrit: $\mu <<{{R}_{b}}M\quad \Rightarrow \quad b\approx \frac{M{{R}_{b}}}{{{k}_{\phi }}N}$.
La deuxième approximation conduit à: $c \approx {k_\phi }N$.
Une solution particulière est: $v = \frac{U_0}{c}$.
On cherche la solution générale de l’équation sans second membre sous la forme: $v = V\exp \left( { - \frac{t}{\tau }} \right)$; on aboutit à l’équation caractéristique: $c{\tau ^2} - b\tau + a = 0$, dont on supposera les racines réelles positives:
$\Delta = b{}^2 - 4ca \ge 0$;${\tau _1}{\tau _2} = \frac{a}{c} > 0$ et :${\tau _1} + {\tau _2} = \frac{b}{c} > 0$.
Il vient alors: ${\tau _1} = \frac{{b - \sqrt {{b^2} - 4ca} }}{{2c}}\;;\quad {\tau _2} = \frac{{b + \sqrt {{b^2} - 4ca} }}{{2c}}$
À partir de la solution: $v\left( t \right) = {V_A}\exp \left( { - \frac{t}{{{\tau _1}}}} \right) + {V_B}\exp \left( { - \frac{t}{{{\tau _2}}}} \right) + {V_C}$, les conditions initiales donnent:
$v\left( {t = 0} \right) = {V_A} + {V_B} + \frac{{{U_0}}}{c}\;;\quad {\left( {\frac{{dv}}{{dt}}} \right)_{t = 0}} = 0 = - \frac{{{V_A}}}{{{\tau _1}}} - \frac{{{V_B}}}{{{\tau _2}}}$
dont on tire: ${V_A} = \frac{{{U_0}}}{c}\frac{{{\tau _1}}}{{{\tau _2} - {\tau _1}}}\;;\quad {V_B} = - \frac{{{U_0}}}{c}\frac{{{\tau _2}}}{{{\tau _2} - {\tau _1}}}$, soit:
${{\tau }_{1}}=\frac{M{{R}_{b}}-\sqrt{{{\left( M{{R}_{b}} \right)}^{2}}-4M{{\left( {{k}_{\phi }}N \right)}^{2}}}}{2{{\left( {{k}_{\phi }}N \right)}^{2}}}\ ;\ {{\tau }_{2}}=\frac{M{{R}_{b}}+\sqrt{{{\left( M{{R}_{b}} \right)}^{2}}-4M{{\left( {{k}_{\phi }}N \right)}^{2}}}}{2{{\left( {{k}_{\phi }}N \right)}^{2}}}\ ;\ {{V}_{C}}=\frac{{{U}_{0}}}{{{k}_{\phi }}N}$
${{V}_{A}}=\frac{{{U}_{0}}}{{{k}_{\phi }}N}\frac{M{{R}_{b}}-\sqrt{{{\left( M{{R}_{b}} \right)}^{2}}-4M{{\left( {{k}_{\phi }}N \right)}^{2}}}}{2\sqrt{{{\left( M{{R}_{b}} \right)}^{2}}-4M{{\left( {{k}_{\phi }}N \right)}^{2}}}}\ ;\ {{V}_{B}}=-\frac{{{U}_{0}}}{{{k}_{\phi }}N}\frac{M{{R}_{b}}+\sqrt{{{\left( M{{R}_{b}} \right)}^{2}}-4M{{\left( {{k}_{\phi }}N \right)}^{2}}}}{2\sqrt{{{\left( M{{R}_{b}} \right)}^{2}}-4M{{\left( {{k}_{\phi }}N \right)}^{2}}}}$
L’hypothèse ${\tau _2} > > {\tau _1}$ implique ${V_A} < < {V_B}$ et $\exp \left( { - \frac{t}{{{\tau _1}}}} \right) < < \exp \left( { - \frac{t}{{{\tau _2}}}} \right)$; par suite:
$v\left( t \right) \approx \frac{{{U_0}}}{{{k_\phi }N}}\left[ {1 - \exp \left( { - \frac{t}{{{\tau _2}}}} \right)} \right]$

3.3.3- Plusieurs essais me conduisent toujours à un $\Delta$négatif, donc à un ${\tau _2}$ complexe, ce qui ne correspond pas à l’esprit dans lequel a été rédigé l’énoncé.
3.4- Analyse finale:
3.4.1- Les constantes de temps ont des ordres de grandeur très différents:
${\tau _e} = 128\;\mu s\quad < < \quad {\tau _m} = 0,218\;s\quad < < \quad {\tau _{th}} = 7,23\;ks$
3.4.2- La question 3.2- conduit au résultat: $a = \frac{{dv}}{{dt}} = \frac{{{F_0}}}{M}$
3.4.3- On calcule donc: ${a_{\max }} = \frac{{{F_{\max }}}}{M} = \left\{ \begin{array}{l}26,4\;mm.{s^{ - 2}}\;pour\;Cu\\58,6\;mm.{s^{ - 2}}\;pour\;Al\end{array} \right.$
3.4.4- De la question 2.3.5.e-, on tire: ${a_{\max C}} = \left\{ \begin{array}{l}0,986\;mm.{s^{ - 2}}\;pour\;Cu\\2,60\;mm.{s^{ - 2}}\;pour\;Al\end{array} \right.$
3.4.5- On constate que c’est l’aluminium qui s’avère le plus intéressant, contrairement à l’idée que l’on a couramment.