Concours Physique ENS de Lyon et Cachan (PC) 2001 (Énoncé)

LC 123 J. 5116
SESSION 2001
______
Filière Physique - Chimie
______
PHYSIQUE
(Épreuve commune aux ENS: Lyon et Cachan)
Durée : 5 heures
______
L'usage de calculatrices électroniques de poche à alimentation autonome, non imprimantes et sans document d'accompagnement, est autorisé. Cependant, une seule calculatrice à la fois est admise sur la table ou le poste travail, et aucun échange n'est autorisé entre les candidats.
Un liquide contenant des particules microscopiques en suspension diffuse la lumière incidente dans toutes les directions. Un objet immergé dans un tel liquide n'est donc pas toujours visible à l'oeil nu. Il peut cependant être détecté par l'analyse du rayonnement transmis dans la direction d'incidence. L'intérêt de cette détection, en imagerie biomédicale par exemple, justifie l'étude du rayonnement diffusé. Dans ce problème, on étudie la diffusion de lumière dans un milieu modèle constitué par une suspension dans l'eau de sphères de polystyrène microscopiques.
Dans la première partie, on étudie le principe d'un modulateur acousto-optique, qui permet de décaler la fréquence d'une onde optique en lui faisant traverser un cristal parcouru par une onde acoustique.
La deuxième partie est consacrée à l'étude d'un dispositif expérimental, utilisant entre autres le modulateur étudié dans la première partie, et permettant l'étude quantitative du phénomène.
On s'intéresse dans la troisième partie au calcul du champ électromagnétique diffusé par une unique sphère de polystyrène, ce qui permet de justifier l'expression de la section efficace de diffusion utilisée dans la deuxième partie.
Les trois parties sont largement indépendantes.
Il est demandé aux candidats de rappeler les numéros identifiant une question avant la solution qu'ils proposent.
Tournez la page S.V.P.

• Notations

• Dans tout le problème, l'espace est rapporté à trois axes Ox, Oy, Oz, auxquels est associée la base orthonormée directe ${\vec e_x}$, ${\vec e_y}$, ${\vec e_z}$ . Le point M de l'espace est repéré par le vecteur $\vec r = \overrightarrow {OM} $ .
• On utilise pour les fonctions sinusoïdales du temps la notation complexe. La fonction réelle $x = {X_m}\cos (\omega t + \varphi )$ sera notée, en omettant, pour alléger l'écriture, le symbole Re (partie réelle) :
$x = {X_m}\exp \left[ {i(\omega t + \varphi )} \right]$
L'amplitude complexe X de x est définie par :
$\underset{\scriptscriptstyle-}{X}={{X}_{m}}\exp (i\varphi )$
On rappelle que la valeur moyenne sur une période $T = \frac{2\pi }{ \omega }$ du produit de deux fonctions sinusoïdales ${x_1}(t) = {X_{1m}}\cos (\omega t + {\varphi _1})$ et ${x_2}(t) = {X_{2m}}\cos (\omega t + {\varphi _2})$ s'exprime simplement en fonction de leurs amplitudes complexes :
$\frac{1}{T}\int_{0}^{T}{{{x}_{1}}(t)\ {{x}_{2}}(t)\ dt=}\frac{1}{2}R\text{e}\left[ {{{\underset{\scriptscriptstyle-}{X}}}_{1}}\underset{\scriptscriptstyle-}{X}_{2}^{*} \right]=\frac{1}{2}R\text{e}\left[ \underset{\scriptscriptstyle-}{X}_{1}^{*}{{{\underset{\scriptscriptstyle-}{X}}}_{2}} \right]$
où ${{\underset{\scriptscriptstyle-}{X}}^{*}}$ désigne le complexe conjugué de X.
• La notation sinc désigne le sinus cardinal défini par : ${\rm{sinc}}(x) = \frac{\sin (x)}{x}$.
• c désigne la vitesse de la lumière dans le vide, ${\varepsilon _0}$ la permittivité du vide, et ${\mu _0}$ la perméabilité du vide.

• Formulaire

${\rm{div}}\,(f\,\vec A) = f\,{\rm{div}}\,\vec A + \overrightarrow {{\rm{grad}}} (f)\,.\,\vec A$ (1)
$\overrightarrow {{\rm{rot}}} \,(f\,\vec A) = f\,\overrightarrow {{\rm{rot}}} \,\vec A + \overrightarrow {{\rm{grad}}} (f)\, \wedge \,\vec A$ (2)
I Modulateur acousto-optique

I.A
On considère deux milieux diélectriques, non magnétiques, homogènes et isotropes, d'indices de réfraction n₁ et n₂ . Le milieu d'indice n₁ occupe le demi-espace z < 0 , le milieu d'indice n₂ le demi-espace z > 0. Le plan z = 0 constitue ainsi un dioptre plan.
Une onde plane progressive, monochromatique de pulsation ω , se propage dans le milieu d'indice n₁ . Le champ électrique ${\vec E_i}$ de cette onde est polarisé rectilignement selon ${\vec e_y}$ ; son vecteur d'onde ${\vec k_i}$ fait avec Oz un angle i (angle d'incidence). On admet que les ondes réfléchies et transmises par le dioptre sont planes, monochromatiques de pulsation ω , de champs électriques ${\vec E_r}$ et ${\vec E_t}$ polarisés selon ${\vec e_y}$.
Les champs électriques, à l'instant t et au point M de l'espace, sont écrits sous la forme
${\vec E_i}(\vec r,t) = {E_0}\,\exp \left[ {i(\omega t - {{\vec k}_i}\,.\,\vec r)} \right]{\vec e_y}$ (3)
${\vec E_r}(\vec r,t) = R\,{E_0}\,\exp \left[ {i(\omega t - {{\vec k}_r}\,.\,\vec r)} \right]{\vec e_y}$ (4)
${\vec E_t}(\vec r,t) = T\,{E_0}\,\exp \left[ {i(\omega t - {{\vec k}_t}\,.\,\vec r)} \right]{\vec e_y}$ (5)
ce qui définit les coefficients de réflexion R et de transmission T en amplitude.
I.A.1 Rappeler, sans les démontrer, les relations de passage du champ électromagnétique à la traversée du dioptre, qu'on exprimera pour $\vec E$ et $\vec B$.
I.A.2 En déduire les lois de la réflexion et de la réfraction de Snell-Descartes (on désignera par i' l'angle de réfraction).
I.A.3 Calculer R en fonction de n₁ , n₂ , i et i'.
I.A.4 On considère dans toute la suite que les indices n₁ et n₂ sont très proches, et on pose:
$n = {n_1} \approx {n_2}$ ,$\delta n = {n_2} - {n_1}$ et $\theta = \frac{\pi}{2 - i}$.
Montrer que le coefficient de réflexion s'écrit alors
$R = - \frac{{\delta n}}{{2n{{\sin }^2}(\theta )}}$ (6)
I.B
On se propose maintenant de montrer que l'onde réfléchie sur un dioptre en mouvement voit sa fréquence décalée par effet Doppler.
I.B.1 Le référentiel R étant associé au trièdre (Oxyz), on considère le référentiel R' en translation par rapport à R à la vitesse $ - V{\vec e_z}$ , auquel on associe le trièdre (O'xyz) avec $\overrightarrow {OO'} = - \,Vt{\vec e_z}$ .
La vitesse V est suffisamment faible devant la vitesse c de la lumière pour que l'on puisse négliger les effets relativistes et considérer que le champ électrique en un point M à l'instant t a la même valeur dans les deux référentiels R et R' .
Le champ électrique d'une onde s'écrit dans R :
$\vec E(\vec r,t) = {E_0}\exp \left[ {i(\omega t - \vec k\,.\,\vec r)} \right]{\vec e_y}$ (7)
Montrer que, dans R' , si l'on pose $\vec r' = \overrightarrow {O'M} $ , ce champ peut s'écrire:
$\vec E(\vec r',t) = {E_0}\exp \left[ {i(\omega 't - \vec k'\,.\,\vec r')} \right]{\vec e_y}$ (8)
et déterminer $\omega '$ et $\vec k'$ en fonction de ω , $\vec k$ et V .
I.B.2 Le dioptre considéré en (I.A.) est éclairé dans les mêmes conditions, mais il se translate maintenant à la vitesse $ - V{\vec e_z}$ , par rapport au référentiel R .
Montrer que, dans R , la pulsation ${\omega _r}$ de l'onde réfléchie est différente de la pulsation ${\omega _i}$ de l'onde incidente, et que le décalage $\Delta \omega = {\omega _r} - {\omega _i}$ vaut :
$\Delta \omega = \frac{{2nV\sin (\theta )}}{c}\omega $ (9)

I.C
Pour réaliser expérimentalement un dispositif permettant, sur ce principe, de décaler la fréquence d'une onde électromagnétique, on peut utiliser la propagation d'une onde acoustique dans un cristal. Une onde acoustique plane, de fréquence f et de longueur d'onde Λ , se propageant selon Oz dans la direction z < 0, induit une modulation de l'indice de réfraction du cristal autour d'une valeur moyenne n_c selon :
$n(z,t) = {n_c} + \Delta n\cos \left[ {2\pi \left( {ft + \frac{z}{\Lambda }} \right)} \right]$ (10)
avec $\Delta n > 0$ et $\Delta n < < {n_c}$. Tournez la page S.V.P.
Pour décrire l'interaction entre l'onde électromagnétique et l'onde acoustique, on adopte le modèle suivant, qui rend correctement compte des observations expérimentales. Le cristal est considéré comme une juxtaposition de petites tranches d'épaisseur $\delta z$ très inférieure à Λ , et donc d'indice pratiquement uniforme. Entre deux tranches successives, il y a un saut d'indice $\delta n = \frac{{\partial n}}{{\partial z}}\delta z$: chaque interface entre deux tranches élémentaires constitue un dioptre plan. Du fait de la propagation de l'onde acoustique, chacun de ces dioptres se déplace à vitesse $\vec V = - \,V{\vec e_z}$ constante.
Le cristal occupe la région de l'espace comprise entre les plans x = -e/2 et x = +e/2 ; on le suppose de grandes dimensions selon Oy et Oz . Le milieu extérieur, homogène, est d'indice n_a . Les faces x = -e/2 et x = +e/2 subissent un traitement anti-reflets : on considérera que les coefficients de transmission à travers ces faces sont égaux à 1.
On éclaire la face x = -e/2 du cristal par une onde plane, de champ électrique
${\vec E_i}(\vec r,t) = {E_0}\exp \left[ {i(\omega t - {{\vec k}_i}\,.\,\vec r)} \right]{\vec e_y}$ (11)
dont le vecteur d'onde ${\vec k_i}$ fait un angle ${\theta _a}$ avec ${\vec e_x}$.
L'amplitude Δn de la variation d'indice étant très faible devant n_c , l'onde réfractée dans le cristal s'y propage presque comme si l'indice était uniformément n_c , : elle est quasi plane, de vecteur d'onde ${\vec k_c}$ faisant avec ${\vec e_x}$ un angle ${\theta _c}$ d'amplitude pratiquement constante et égale à E₀. Cependant, chaque interface entre deux tranches élémentaires du cristal réfléchit une onde élémentaire, d'amplitude très faible devant E₀ (figure 1). Ces ondes élémentaires émergent du cristal en x = +e/2. Leur superposition, dans l'air, constitue l'onde réfléchie.

I.C.1 On considère un plan Σ orthogonal à la direction de l'onde réfléchie. Calculer, au niveau de Σ , le déphasage $\varphi ({z_i})$ entre l'onde élémentaire réfléchie par l'interface z = z_i et celle réfléchie en z = 0. On exprimera $\varphi ({z_i})$ en fonction de la longueur d'onde λ₀ dans le vide de l'onde incidente et on négligera évidemment pour ce calcul la célérité des ondes acoustiques devant celle de la lumière.
I.C.2 Les interfaces atteintes par l'onde incidente sont comprises entre z = -L/2 et z = +L/2. Montrer que l'amplitude complexe du champ total réfléchi peut se mettre sous la forme .
$\underset{\scriptscriptstyle-}{E}=K\exp (i\psi )\left\{ \exp \left[ i\alpha (t) \right]\text{sinc}\left[ \pi \text{L}\left( \frac{\text{1}}{\Lambda }-\frac{2{{n}_{a}}\sin ({{\theta }_{a}})}{{{\lambda }_{0}}} \right) \right]-\exp \left[ -i\alpha (t) \right]\text{sinc}\left[ \pi \text{L}\left( \frac{\text{1}}{\Lambda }+\frac{2{{n}_{a}}\sin ({{\theta }_{a}})}{{{\lambda }_{0}}} \right) \right] \right\}$
où K est un réel positif et $\psi $ un déphasage arbitraire dépendant du choix de Σ .
Préciser les expressions de K et α(t) en fonction des données.
I.C.3 Montrer que les deux termes contribuant à l'amplitude du champ réfléchi sont respectivement maximaux pour deux valeurs de ${\theta _a}$ opposées, notées respectivement ${\theta _B}$ et $ - {\theta _B}$ (angles de Bragg). On négligera pour cela la variation de K avec ${\theta _a}$ , et on justifiera a posteriori cette approximation, compte tenu des ordres de grandeur des différents paramètres
$L \approx 1mm$ $\Lambda \approx 50\mu m$ ${n_c} \approx 2$ ${\lambda _0} \approx 600nm$
Représenter l'allure de la variation avec sin(${\theta _a}$) de l'intensité lumineuse émergente.

I.C.4 Vérifier qu'à l'incidence de Bragg les ondes élémentaires réfléchies par l'interface en z = z_i et par celle en z = z_i + Λ interférent constructivement.
I.C.5 On envisage séparément ${\theta _a} = + {\theta _B}$ et${\theta _a} = - {\theta _B}$ représentés sur la figure 2 :

Montrer que l'onde optique réfléchie est décalée en fréquence de
$\frac{{\Delta \omega }}{{2\pi }} = \pm f$
avec un signe que l'on précisera pour chacune des deux configurations, et expliquer pourquoi ce décalage de fréquence est cohérent avec le résultat établi à la question (I.B.2).
Il Etude d'un dispositif expérimental
Un interféromètre de Mach-Zehnder, représenté sur la figure 3, est constitué de deux lames semi-transparentes identiques (L_E ) et (L_S ), et de deux miroirs de renvoi (M₁) et (M₂).
On éclaire la lame d'entrée (L_E) par le faisceau d'un laser hélium-néon, de longueur d'onde dans le vide λ₀ = 632, 8 nm et de pulsation $\omega = \frac{2\pi c}{{\lambda }_{0}}$.
Le faisceau transmis par (L_E ) traverse ensuite un modulateur acousto-optique, du type de celui étudié dans la première partie, dont l'effet est de décaler la fréquence du rayonnement. Ce modulateur est alimenté par un générateur de radiofréquences (R.F) , de fréquence f = 50 MHz, qui délivre un signal $m(t) = {m_0}\cos (2\pi \,ft)$ . Les ondes acoustiques produites ont ainsi la fréquence f . Comme on l'a montré dans la première partie, l'onde lumineuse émergeant du modulateur a alors pour pulsation $\omega + \Delta \omega $ , avec :
$\Delta \omega = 2\pi \,f$
Le faisceau est ensuite réfléchi sur (M₁ ) puis sur (L_S ). On désignera dans la suite par "bras de référence" le bras correspondant de l'interféromètre. Dans l'autre bras, que l'on appelera "bras de mesure", le faisceau réfléchi par (L_E) est ensuite réfléchi par (M₂) puis transmis par (Ls)
Tournez la page S.V.P.

L'interféromètre est réglé de telle façon que les deux faisceaux soient ensuite superposés au niveau d'un détecteur, qui délivre un signal électrique s(t) proportionnel à la puissance totale P(t) qu'il reçoit sur sa fenêtre d'entrée :
$s(t) = \eta P(t)$ (12)

II.A
La fenêtre d'entrée du détecteur est un carré de côté b, orthogonal à Oz et correspondant dans le plan Oxy à -b/2 < x < +b/2 et -b/2 < y < +b/2.
On désigne par ${\vec E_0}$ le champ électrique de l'onde provenant du bras de référence, et par ${\vec E_1}$ le champ provenant du bras de mesure. Au niveau du détecteur, ces deux champs s'écrivent :
${\vec E_0}(\vec r,t) = {E_0}\exp i\left[ {(\omega + \Delta \omega )t - {{\vec k}_0}\,.\,\vec r + {\varphi _0}} \right]{\vec e_y}$ (13)
${\vec E_1}(\vec r,t) = {E_1}\exp i\left[ {\omega t - {{\vec k}_1}\,.\,\vec r + {\varphi _1}} \right]{\vec e_y}$ (14)
On notera I₀ et I₁ les intensités correspondantes.
II.A.1 On suppose que les deux faisceaux émergeant de l'interféromètre sont parfaitement alignés, se propageant selon Oz. Calculer s(t) en fonction de I₀ et I₁ et montrer que l'on doit détecter un signal de battement à la fréquence f.
II.A.2 Du fait de l'inévitable imperfection du réglage de l'interféromètre, les faisceaux font en réalité entre eux un petit angle α , au niveau du détecteur. On considérera, par exemple, que l'un des faisceaux arrive sur la fenêtre sous incidence normale et l'autre sous incidence α . Que devient l'amplitude du signal de battement détecté ? Conclure.
II.A.3 La largeur de la fenêtre est b = 2 mm. Quelle valeur de l'angle α entre les deux faisceaux peut-on tolérer pour ne pas être gêné par le problème mis en évidence à la question précédente ? On supposera dans la suite que l'alignement est convenablement réalisé.
II.B
On cherche maintenant à mesurer l'amplitude du signal de battement à l'aide du dispositif électronique schématisé sur la figure 4, qui comprend deux multiplieurs analogiques et un filtre passe-bas de fréquence de coupure f_C .
Les signaux d'entrée du premier multiplieur sont le signal s(t) délivré par le photodétecteur et le signal de référence m(t) délivré par le générateur RF qui alimente aussi le modulateur.

II.B.1 Montrer qu'un choix judicieux de la valeur de f_c, permet d'obtenir un signal de sortie S₁ proportionnel à I₁ .
II.B.2 Le signal S₁ est très sensible aux perturbations extérieures, et peut varier simplement parce que l'on tapote un des miroirs de renvoi de l'interféromètre. Expliquer pourquoi.
Pour remédier à cet inconvénient, on produit un signal S₂ à l'aide d'un dispositif électronique parfaitement similaire, mais en remplaçant à l'entrée du premier multiplieur la référence m(t) par $m'(t) = {m_0}\sin (2\pi \,ft)$.
II.B.3 Comment peut-on, en pratique, obtenir le signal $m'(t)$ à partir du signal m(t) ?
II.B.4 Montrer que l'on peut effectivement, en utilisant S₁ et S₂ , produire un signal S qui ne soit plus aussi sensible aux perturbations extérieures et qui soit toujours proportionnel à I₁ .

II.C
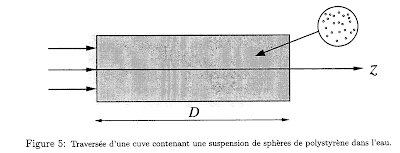
On introduit dans le bras de mesure de l'interféromètre une cuve remplie d'une suspension de sphères de polystyrène microscopiques dans l'eau (figure 5). L'épaisseur de liquide traversée par le faisceau, dans la direction Oz , est D = 10 cm : la lumière pénètre dans la cuve en z = 0 et en ressort en z = D . L'indice de l'eau pour la longueur d'onde λ₀ est n_e = 1,33 ; celle du polystyrène n_p = 1,59. Chaque sphère diffuse la lumière, ce qui confère au liquide un aspect laiteux.
II.C.1 Expliquer pourquoi on n'attend pas, au niveau du détecteur, de signal de battements entre la lumière diffusée par la cuve et le faisceau de référence.
Quel problème de cohérence se pose-t-il ici ? On pourra s'appuyer sur les résultats de (II.A).
On observe cependant un phénomène de battements, mais il correspond aux interférences entre le faisceau de référence et la partie de la lumière qui a traversé la cuve en ligne droite et émerge dans la direction d'incidence. On appelle intensité cohérente I_C l'intensité lumineuse correspondant à cette lumière. Le signal S permet de mesurer directement l'intensité cohérente I_C à la sortie de la cuve.
Tournez la page S.V.P.

II.C.2 Montrer que, à l'intérieur de la cuve, I_C est fonction de z et vérifie l'équation :
$\frac{{d\,{I_c}(z)}}{{dz}} = - v\,{\sigma _d}\,{I_c}(z)$ (15)
où v est le nombre de sphères par unité de volume et ${\sigma _d}$ la section efficace de diffusion, définie comme le rapport entre la puissance P_d diffusée par une sphère et l'intensité incidente I_c sur cette sphère :
${\sigma _d} = \frac{{{P_d}}}{{{I_c}}}$ (16)
En déduire que l'intensité cohérente I_c(D) à la sortie de la cuve vérifie :
${I_c}(d) = {I_{c0}}\exp ( - v{\kern 1pt} {\sigma _d}{\kern 1pt} D)$ (17)
Que représente ${I_{c0}}$ ?
II.C.3 Le tableau 1 donne les valeurs expérimentales de $\ln \left[ {\frac{{{I_c}(D)}}{{{I_{c0}}}}} \right]$ mesurées pour différentes
valeurs de la fraction volumique de polystyrène, c'est-à-dire du rapport entre le volume de polystyrène et le volume total de la solution :

Commenter ces valeurs numériques.
La section efficace de diffusion ${\sigma _d}$ est fonction de n_e , n_p , λ₀ et du volume V des sphères:
${\sigma _d} = 24{\pi ^3}{\left( {\frac{{{n_e}}}{{{\lambda _0}}}} \right)^4}{\left( {\frac{{n_p^2 - n_e^2}}{{n_p^2 + 2n_e^2}}} \right)^2}{V^2}$ (18)
Déterminer le rayon a des sphères utilisées.
II.C.4 Les incertitudes relatives sur les mesures des intensités sont de 1 % ; celles sur les fractions volumiques de 0,5 %. Evaluer l'incertitude Δa sur le rayon des sphères.
III Diffusion de la lumière par une particule sphérique
Dans cette partie, on se propose de justifier l'expression de la section efficace de diffusion ${\sigma _{\rm{d}}}$ utilisée à la question (II.C.3).

III.A
On considère une sphère, de rayon a , de polarisation $\vec P$ uniforme, dans le vide. On veut calculer le champ électrostatique créé par cette distribution de polarisation.
III.A.1 Montrer que le champ créé par la polarisation $\vec P$ est identique à celui que créerait une distribution surfacique de charges ${\sigma _{{\rm{lié }}}}$ , que l'on précisera.
III.A.2 Montrer que l'on peut retrouver cette distribution surfacique de charges en superposant deux sphères de même rayon a , uniformément chargées, de densité volumique de charge respectivement + ρ et - ρ, centrées en deux points infiniment voisins, respectivement O₊ et O_- Etablir la relation liant $\vec P$, ρ , O₊ et O_- .
III.A.3 Donner l'expression du potentiel électrostatique V_ρ créé en tout point M de l'espace par une sphère de rayon a et de centre O, de densité de charge uniforme ρ . On prendra le potentiel nul lorsque M est à l'infini.
III.A.4 Déduire des résultats précédents l'expression du potentiel ${V_{\vec P}}$ à l'intérieur de la sphère uniformément polarisée; montrer que le champ ${\vec E_{\vec P}}$ orrespondant est uniforme et vaut :
${\vec E_{\vec P}} = - \frac{{\vec P}}{{3{\varepsilon _0}}}$ (19)
III.B
On considère maintenant une sphère de polystyrène, de rayon a et de centre O , dans le vide. Le polystyrène est un matériau isotrope, d'indice de réfraction n_P ; on notera ε_p sa permittivité diélectrique absolue.
On envoie sur la sphère une onde électromagnétique plane, monochromatique de pulsation ω, de champ électrique :
${\vec E_i}(\vec r,t) = {\vec E_{i0}}\exp \left[ {i(\omega t - \vec k\,.\,\vec r)} \right]$ (20)
On cherche à déterminer le champ électromagnétique $({\vec E_d},{\vec B_d})$ diffusé par la sphère, et défini par les relations :
$\vec E = {\vec E_i} + {\vec E_d}$ et $\vec B = {\vec B_i} + {\vec B_d}$ (21)
où $(\vec E,\vec B)$ représente le champ électromagnétique total et $({\vec E_i},{\vec B_i})$ le champ incident.

III.B.1 On note $({\vec E^{{\mathop{\rm int}} }},{\vec B^{{\mathop{\rm int}} }})$ et $({\vec E^{{\rm{ext}}}},{\vec B^{{\rm{ext}}}})$ les champs respectivement à l'intérieur et à l'extérieur de la sphère.
Ecrire les équations de Maxwell pour ces champs.
III.B.2 Exprimer les relations de passage vérifiées par $\vec E$ et $\vec B$ à la surface de la sphère.
III.B.3 Vérifier que, à l'extérieur de la sphère, le champ diffusé $({\vec E_d},{\vec B_d})$ vérifie simplement les équations de Maxwell dans le vide.
Tournez la page S.V.P.
III.B.4 Montrer que, à l'intérieur de la sphère, le champ diffusé vérifie aussi les équations de Maxwell dans le vide, à condition d'y introduire une distribution volumique de courant ${\vec j_{{\rm{lié }}}}$ dont on exprimera l'amplitude complexe ${{\underset{\scriptscriptstyle-}{\vec{j}}}_{\text{li }\!\!\acute{\mathrm{e}}\!\!\text{ }}}$ en fonction de celle du champ total ${\vec E^{{\mathop{\rm int}} }}$ à l'intérieur de la sphère.
III.B.5 Montrer qu'on peut alors considérer le champ diffusé comme le champ créé dans le vide par la distribution de courant ${\vec j_{{\rm{li\'e }}}}$ à condition de rajouter une distribution surfacique de charges ${\sigma _{{\rm{li\'e }}}}$ que l'on déterminera.
III.B.6 Montrer enfin que le champ créé par cette distribution de charges et de courants est équivalent au champ qui serait créé par une sphère polarisée, de polarisation :
$\vec P = ({\varepsilon _p} - {\varepsilon _0}){\vec E^{{\mathop{\rm int}} }}$ (22)
III.C
On introduit le potentiel scalaire V_d et le potentiel vecteur ${\vec A_{\rm{d}}}$ associés au champ diffusé $({\vec E_d}\,,\,{\vec B_d})$.
On impose à ces potentiels de vérifier, en tout point de l'espace, la condition de jauge de Lorentz :
${\rm{div}}\,({\vec A_{\rm{d}}}) + \frac{1}{{{c^2}}}\frac{{\partial {V_{\rm{d}}}}}{{\partial {\rm{t}}}} = 0$ (23)
On montre, à l'aide des équations de Maxwell, que ${{\underset{\scriptscriptstyle-}{\vec{A}}}_{\text{d}}}$ satisfait l'équation
$\Delta \,{{\vec{A}}_{\text{d}}}+{{\mu }_{0}}{{\varepsilon }_{0}}{{\omega }^{2}}{{\vec{A}}_{\text{d}}}=-{{\mu }_{0}}{{\underset{\scriptscriptstyle-}{\vec{j}}}_{\text{li }\!\!\acute{\mathrm{e}}\!\!\text{ }}}$ (24)
dont la solution est :
${{\underset{\scriptscriptstyle-}{\vec{A}}}_{\text{d}}}(\vec{r})=\frac{{{\mu }_{0}}}{4\pi }\iiint_{\text{espace}}{{{{\underset{\scriptscriptstyle-}{\vec{j}}}}_{\text{li }\!\!\acute{\mathrm{e}}\!\!\text{ }}}}(\vec{r}')\frac{\exp (-ik\left\| \vec{r}-\vec{r}' \right\|}{\left\| \vec{r}-\vec{r}' \right\|}{{d}^{3}}r'$ (25)
où k est le nombre d'onde défini par $k = \frac{2 \pi }{\lambda _{0}} = \frac{\omega}{c}$ . La notation d³ r', représente un volume élémentaire autour du point M' tel que $\overrightarrow {OM'} = \vec r'$ .
III.C.1 Cette solution est appelée solution des potentiels retardés. Pourquoi ?
On a vu en (III.B.4.) que ${\vec j_{{\rm{lié }}}}$ était fonction de $\vec E$ , lequel n'est pas connu a priori puisqu'il dépend de ${\vec E_{\rm{d}}}$ qui dépend lui-même de ${\vec A_{\rm{d}}}$ ... La résolution dans le cas général apparaît donc délicate.
On se limite dans toute la suite au cas particulier plus simple où la sphère est de rayon très petit devant la longueur d'onde du rayonnement : a << λ₀ . Cette restriction permet, entre autres, de considérer que le champ incident est pratiquement uniforme à l'intérieur de la sphère. Il est alors tentant de chercher, pour $\vec E$ et ${\vec E_{\rm{d}}}$ une solution correspondant à une polarisation $\vec P$ uniforme dans le volume de la sphère. Il faudra évidemment ensuite vérifier à posteriori la compatibilité de la solution obtenue avec cette hypothèse.

III.C.2 Montrer que, dans ces conditions, l'intégrale permettant le calcul de ${{\underset{\scriptscriptstyle-}{\vec{A}}}_{\text{d}}}^{\operatorname{int}}$ a la même forme
que celle correspondant au potentiel électrostatique créé par une sphère uniformément chargée. En déduire l'expression de ${{\underset{\scriptscriptstyle-}{\vec{A}}}_{\text{d}}}^{\operatorname{int}}$ .
III.C.3 Calculer ${{\underset{\scriptscriptstyle-}{V}}_{\text{d}}}^{\operatorname{int}}$ puis les amplitudes complexes ${{\vec{\underset{\scriptscriptstyle-}{E}}}_{\text{d}}}^{\operatorname{int}}$ et ${{\underset{\scriptscriptstyle-}{\vec{B}}}_{\text{d}}}^{\operatorname{int}}$ des champs diffusés.
III.C.4 Exprimer ${\vec E_{\rm{d}}}^{{\mathop{\rm int}} }$ et ${\vec B_{\rm{d}}}^{{\mathop{\rm int}} }$ en fonction du champ incident ${\vec E_i}$ .
Cette solution est-elle cohérente avec l'hypothèse d'uniformité de $\vec P$ ?
IILD
On cherche maintenant à déterminer le champ ${\vec E_{\rm{d}}}$ diffusé en un point M situé à une distance r de la sphère de polystyrène très grande devant la longueur d'onde : r >> λ₀ .
III.D.1 Montrer que la solution des potentiels retardés peut alors s'écrire :
 ${{\underset{\scriptscriptstyle-}{\vec{A}}}_{\text{d}}}(\vec{r})={{\underset{\scriptscriptstyle-}{\vec{A}}}_{0}}\frac{\exp (-ikr)}{r}$ (26)
ou ${{\underset{\scriptscriptstyle-}{\vec{A}}}_{0}}$ est une constante vectorielle que l'on exprimera en fonction de a et ${{\underset{\scriptscriptstyle-}{\vec{j}}}_{\text{li }\!\!\acute{\mathrm{e}}\!\!\text{ }}}$ .
III.D.2 Pour repérer la position du point M , on introduit le système de coordonnées sphériques de pôle O et d'axe polaire Oz , tel que ${{\underset{\scriptscriptstyle-}{\vec{A}}}_{0}}={{A}_{0}}\,{{\vec{e}}_{z}}$ . On a ainsi $\theta = ({\vec A_0},\vec r)$ . Etablir les expressions de ${{\underset{\scriptscriptstyle-}{V}}_{\text{d}}}$ et ${{\underset{\scriptscriptstyle-}{\vec{E}}}_{\text{d}}}$ en projection sur la base $({\vec e_r},\,{\vec e_\theta },\,{\vec e_\varphi })$ associée.
IILD.3 Montrer qu'au voisinage de $\vec r = {\vec r_0}$ , le champ ${\vec E_{\rm{d}}}$ a pratiquement une structure d'onde plane (on posera $\vec r = {\vec r_0} + \vec \delta $) . En déduire que l'intensité moyenne (puissance surfacique moyenne) diffusée dans la direction de $\vec r$ est proportionnelle à ${{\left\| {{{\underset{\scriptscriptstyle-}{\vec{E}}}}_{\text{d}}} \right\|}^{2}}$ avec un coefficient de proportionnalité que l'on exprimera en fonction de c et ε₀ .

IILD.4 Déduire du résultat précédent la puissance moyenne totale ${P_d}$ diffusée par la sphère en fonction de A₀ .
III.D.5 En utilisant les relations démontrées en (III.D.1), (III.B.4) et (III.C.4), exprimer ${P_d}$ en fonction de ${{\left\| {{{\underset{\scriptscriptstyle-}{\vec{E}}}}_{i}} \right\|}^{2}}$ .
IILD.6 Exprimer l'intensité I_i du champ incident en fonction de ${{\left\| {{{\underset{\scriptscriptstyle-}{\vec{E}}}}_{i}} \right\|}^{2}}$ . On définit la section efficace de diffusion ${\sigma _{\rm{d}}}$ par :
${P_d} = {\sigma _{\rm{d}}}\,{I_i}$ (27)
Montrer que, si V représente le volume de la sphère de polystyrène, on a:
${\sigma _{\rm{d}}} = 24{\pi ^3}\frac{1}{{\lambda _0^4}}{\left( {\frac{{{\varepsilon _p} - {\varepsilon _0}}}{{{\varepsilon _p} + 2{\varepsilon _0}}}} \right)^2}\,{V^2}$ (28)
IILD.7 Comparer le résultat obtenu à l'expression de ${\sigma _{\rm{d}}}$ donnée en (ILC.3).

Concours Physique Modélisation ENS de Cachan et École Polytechnique (PSI) 2001 (Corrigé)

MODÉLISATION EN SCIENCES PHYSIQUES ET SCIENCES DE L’INGÉNIEUR

Durée: 5 heures

2001

ANALYSE ÉLECTROMAGNÉTIQUE

La conductivité σ et la perméabilité μ du milieu conducteur sont considérées comme constantes et uniforme tout au long du problème. ¹.

Étude préliminaire

A partir de l’équation de Maxwell-Ampère considérée dans l’approximation des régimes quasi-permanents:
$$\mathrm{ {{{\overrightarrow{\vphantom{(^{1}}\mathrm{\mathrm{rot}}}}\,\mathrm{}}}\,{\overrightarrow{\vphantom{(^{1}}\mathrm{h}}}={\overrightarrow{\vphantom{(^{1}}\mathrm{j}}}}\:\:\: \text{(loi d'Amp{\`e}re)} \label{Ampere}$$
nous obtenons en prenant le rotationnel des deux membres:
$$\mathrm{{{{\overrightarrow{\vphantom{(^{1}}\mathrm{\mathrm{rot}}}}\,\mathrm{}}}{{{\overrightarrow{\vphantom{(^{1}}\mathrm{\mathrm{rot}}}}\,\mathrm{}}}{\overrightarrow{\vphantom{(^{1}}\mathrm{h}}}={{{\overrightarrow{\vphantom{(^{1}}\mathrm{\mathrm{grad}}}}\,\mathrm{}}}{{\mathrm{div}\,\mathrm{{\overrightarrow{\vphantom{(^{1}}\mathrm{h}}}}}}-\Delta {\overrightarrow{\vphantom{(^{1}}\mathrm{h}}} ={{{\overrightarrow{\vphantom{(^{1}}\mathrm{\mathrm{rot}}}}\,\mathrm{{\overrightarrow{\vphantom{(^{1}}\mathrm{j}}}}}}}.$$
La divergence du champ $ \mathrm{{\overrightarrow{\vphantom{(^{1}}\mathrm{h}}}} $ est nulle car il est dirigé selon y et ne dépend que de x:
$$\mathrm{{{\mathrm{div}\,\mathrm{{\overrightarrow{\vphantom{(^{1}}\mathrm{h}}}}}}=\frac{\partial h_{x}}{\partial x}+ \frac{\partial h_{y}}{\partial y} +\frac{\partial h_{z}}{\partial z}=\frac{\partial}{\partial y}h(x,t)=0}.$$
De même, le calcul du laplacien vectoriel se réduit à:
$$\mathrm{\Delta {\overrightarrow{\vphantom{(^{1}}\mathrm{h}}}=\frac{\partial^{2}h}{\partial x^{2}}{\overrightarrow{\vphantom{(^{1}}\mathrm{y}}}}.$$
La conductivité étant uniforme:
$$\mathrm{{{{\overrightarrow{\vphantom{(^{1}}\mathrm{\mathrm{rot}}}}\,\mathrm{{\overrightarrow{\vphantom{(^{1}}\mathrm{j}}}}}}=\sigma {{{\overrightarrow{\vphantom{(^{1}}\mathrm{\mathrm{rot}}}}\,\mathrm{{\overrightarrow{\vphantom{(^{1}}\mathrm{e}}}}}} =-\sigma \frac{\partial {\overrightarrow{\vphantom{(^{1}}\mathrm{b}}}}{\partial t} =-\sigma\mu\frac{\partial {\overrightarrow{\vphantom{(^{1}}\mathrm{h}}}}{\partial t}}.$$
Il nous reste donc, en projetant sur l’axe $ \mathrm{\vec{y}} $ l’équation aux dérivées partielles:
$$\mathrm{\frac{\partial^{2}h}{\partial x^{2}} -\sigma\mu\frac{\partial h}{\partial t}=0}.$$
Il nous suffit alors de rechercher une solution de la forme:
h(x, t)=Re{H(x)exp(iω t)} avec H(x)∈ℂ
en la reportant dans l’équation précédente nous obtenons:
$$\mathrm{ \frac{\partial^{2}H}{\partial x^{2}}-i\sigma\mu\omega\,H=0}. \label{Aeq8}$$

On vérifie immédiatement que:
(1+i)² = 2i,
par conséquent:
$$\mathrm{i\sigma \mu \omega=\left(1+i\right)^{2}\left(\sqrt{\frac{\sigma \omega \mu}{2}}\right)^{2}=\left(\frac{1+i}{\delta}\right)^{2},}$$
d’où l’équation:
$$\mathrm{\frac{\partial^{2}H}{\partial x^{2}}-\left(\frac{1+i}{\delta}\right)^{2}H=0} \label{Aeq9}$$

La solution générale de l’équation précédente est:
$$\mathrm{H(x)=C_{1}\exp\left[\left(1+i\right)\frac{x}{\delta}\right] +C_{2}\exp\left[-\left(1+i\right)\frac{x}{\delta}\right]}.$$
où C₁ et C₂ sont deux constantes arbitraires.
Les deux conditions aux limites à vérifier sont:
H(x = 0)=H₀ et lim_{x → ∞} = 0.

L’application de la condition aux limites lorsque x → ∞ impose à C₁ d’être nulle, ce qui permet ensuite d’identifier C₂ à H₀ en étudiant la valeur à l’origine:
$$\mathrm{H(x)=H_{0}\exp\left[-\left(1+i\right)\frac{x}{\delta}\right]}.$$
Il vient donc, en passant à la notation réelle:
$$\mathrm{h(x,t)=Re\left\{H(x)\exp (i\omega\,t)\right\} =H_{0}\exp\left(-\frac{x}{\delta}\right) \cos\left(\omega\,t-\frac{x}{\delta}\right)}.$$

Nous obtenons cette densité de courant à partir de l’équation [Ampere]:
$$\mathrm{{\overrightarrow{\vphantom{(^{1}}\mathrm{j}}}={{{\overrightarrow{\vphantom{(^{1}}\mathrm{\mathrm{rot}}}}\,\mathrm{{\overrightarrow{\vphantom{(^{1}}\mathrm{h}}}}}}={{{\overrightarrow{\vphantom{(^{1}}\mathrm{\mathrm{rot}}}}\,\mathrm{}}}\left(h(x,t){\overrightarrow{\vphantom{(^{1}}\mathrm{y}}}\right) =\frac{\partial h}{\partial x}{\overrightarrow{\vphantom{(^{1}}\mathrm{z}}}},$$
il vient, en projection sur $ {\overrightarrow{\vphantom{(^{1}}\mathrm{z}}} $:
$$\mathrm{j(x,t)=\frac{H_{0}}{\delta}\exp\left(-\frac{x}{\delta}\right) \left[\sin\left(\omega\,t-\frac{x}{\delta}\right) -\cos\left(\omega\,t-\frac{x}{\delta}\right)\right].}$$

La quantité δ est homogène à une longueur appelée “épaisseur de peau” car elle caractérise l’ordre de grandeur de l’épaisseur de la région dans laquelle circule un courant électrique. On peut aussi dire qu’elle caractérise la profondeur à laquelle pénètre le champ magnétique créé par le bobinage extérieur.

La puissance volumique dissipée donnée par:
$$\mathrm{p(x,t)=\frac{1}{\sigma}j^{2}(x,t)} \label{Aeq10}$$
a pour valeur:
$$\mathrm{p(x,t)=\frac{H_{0}^{2}}{\sigma \delta^{2}} \exp\left(-2\frac{x}{\delta}\right) \left[1-2\sin\left(\omega\,t-\frac{x}{\delta}\right) \cos\left(\omega\,t-\frac{x}{\delta}\right)\right].}$$
Nous remanions légèrement ce résultat compte tenu de l’expression de δ et d’une formule trigonométrique bien connue:
$$\mathrm{p(x,t)=\frac{\mu\omega H_{0}^{2}}{2} \exp\left(-2\frac{x}{\delta}\right)\left[1- \sin\left(2\omega\,t-2\frac{x}{\delta}\right)\right].}$$

La moyenne temporelle Q(x) sur une période de p(x, t) :
$$\mathrm{Q(x)=\frac{1}{T_{e}}\int_{0}^{T_{e}}p(x,t)dt} \label{Aeq11}$$
se calcule immédiatement en remarquant que la valeur moyenne temporelle du sinus est nulle, il reste donc:
$$\mathrm{Q(x)=\frac{H_{0}^{2}}{\sigma\delta^{2}} \exp\left(-2\frac{x}{\delta}\right) =\frac{\mu\omega H_{0}^{2}}{2} \exp\left(-2\frac{x}{\delta}\right)}.$$

La puissance totale dissipée par unité de surface de la barre est simplement donnée par:
Q_tot = ∫₀^∞Q(x).dx.
Comme il vient:
$$\mathrm{\int_{0}^{\infty}\exp\left(-2\frac{x}{\delta}\right)dx =-\frac{\delta}{2}\left[\exp\left(-2\frac{x}{\delta}\right)\right]_{0}^{\infty} =\frac{\delta}{2}},$$
nous obtenons le résultat suggéré par l’énoncé:
$$\mathrm{Q_{tot}=\frac{1}{2\sigma}\frac{H_{0}^{2}}{\delta}}. \label{Aeq12}$$
Nous pouvons mettre ce résultat sous la forme:
$$\mathrm{Q_{tot}=\frac{\mu H_{0}^{2}\omega \delta}{4}}.$$
Sous cette forme, nous identifions une densité volumique d’énergie (électromagnétique) μH₀², cette énergie est multipliée par ω qui est l’inverse d’un temps, nous obtenons donc une puissance volumique ωμH₀², qui multipliée par une longueur δ conduit à une puissance surfacique, ce que nous recherchions. Le résultat est donc homogène.

Etude d’une plaque de largeur 2a:

Le champ magnétique est par hypothèse parallèle à la direction $ \mathrm{{\overrightarrow{\vphantom{(^{1}}\mathrm{y}}}} $ et n’est fonction que de x, les conditions aux limites étant les mêmes en x = a et x = −a, le principe de Curie conduit à la recherche de solutions h(x, t) fonctions paires de x. Comme la dérivée par rapport à x d’une fonction paire en x est une fonction impaire de x et qu’une fonction (continue) impaire est nécessairement nulle en x = 0: $ \mathrm{\displaystyle {\frac{\partial h}{\partial x}(0,t)=0}} $.

La solution proposée est de la forme obtenue à la question [A.1.3.], c’est donc une solution de l’équation électromagnétique [Aeq8]. De plus, il apparaît immédiatement que:
h(−a, t)=h(a, t)=H₀cos(ω t).
(C’est évident pour x = a et il suffit d’écrire la définition du cosinus hyperbolique:
$$\mathrm{ch\left(\frac{1+i}{\delta}x\right) =\frac{1}{2}\left[\exp\left(\frac{1+i}{\delta}x\right) +\exp\left(-\frac{1+i}{\delta}x\right)\right]}$$
pour établir la relation en x = −a).

La dérivation est une opération linéaire, par conséquent nous pouvons l’effectuer sur la représentation complexe, ce qui nous donne à partir de l’expression:
$$\mathrm{h(x,t)=Re\left[H(x)\exp \left(i\omega\,t\right)\right]\:\: \text{avec}\:H(x)=H_{0}\frac{ch{\displaystyle \frac{\left(1+i\right)x}{\delta}}}{ch{\displaystyle \frac{\left(1+i\right)a}{\delta}}}}.$$

$$\mathrm{j(x,t)=Re\left[J(x)\exp \left(i\omega\,t\right)\right]\:\: \text{avec}\:J(x)=(1+i)\frac{H_{0}}{\delta}\frac{sh{\displaystyle \frac{\left(1+i\right)x}{\delta}}}{ch{\displaystyle \frac{\left(1+i\right)a}{\delta}}}}.$$

Le calcul de la densité volumique de puissance ne peut se faire qu’en notation réelle puisque l’opération à effectuer est non linéaire, par conséquent, en notant la densité de courant complexe J(x, t):
$$\mathrm{J(x,t)=\frac{1+i}{\delta}H_{0}\frac{sh{\displaystyle \frac{\left(1+i\right)x}{\delta}}}{ch{\displaystyle \frac{\left(1+i\right)a}{\delta}}}.\exp \left(i\omega\,t\right)},$$
il vient:
$$\mathrm{p(x,t)=\frac{1}{4\sigma}\left[J(x,t)+J^{*}(x,t)\right]^{2}}.$$
soit:
$$\mathrm{p(x,t)=\frac{H_{0}^{2}}{4\sigma\delta^{2}}\left[ \left(1+i\right)\frac{sh{\displaystyle \frac{\left(1+i\right)x}{\delta}}}{ch{\displaystyle \frac{\left(1+i\right)a}{\delta}}}\exp \left(i\omega\,t\right)+ \left(1-i\right)\frac{sh{\displaystyle \frac{\left(1-i\right)x}{\delta}}}{ch{\displaystyle \frac{\left(1-i\right)a}{\delta}}}\exp \left(-i\omega\,t\right) \right]^{2}}.$$

Pour calculer la moyenne temporelle de p(x, t), nous devons intégrer sur une période une expression de la forme:
φ = [Aexp(iω t)+A^*exp(−iω t)]²,
qui se développe en une somme de deux termes réels:
$$\mathrm{\varphi=\underbrace{\mathrm{A^{2}\exp\left(2i\omega\;t\right) +A^{*2}\exp\left(-2i\omega\;t\right)}}+2A.A^{*}.}$$
Le premier terme est une fonction sinus de fréquence double de la fréquence du champ magnétique, il est donc de valeur moyenne nulle sur une période, seul le second terme intervient dans le résultat de l’intégration. Ce second terme étant indépendant du temps, il est égal à sa valeur moyenne, nous en déduisons donc que:
$$\mathrm{Q(x)=\frac{H_{0}^{2}}{2\sigma}(1+i)(1-i)\frac{sh{\displaystyle \frac{\left(1+i\right)x}{\delta}}}{ch{\displaystyle \frac{\left(1+i\right)a}{\delta}}}.\frac{sh{\displaystyle \frac{\left(1-i\right)x}{\delta}}}{ch{\displaystyle \frac{\left(1-i\right)a}{\delta}}}}.$$
Nous pouvons alors passer à la représentation réelle, en effet:
$$\mathrm{ch\left(\frac{1-i}{\delta}a\right) =\frac{1}{2}\left[\exp\left(\frac{1-i}{\delta}a\right) +\exp\left(-\frac{1-i}{\delta}x\right)\right]},$$

On vérifie sans difficulté que:
$$\mathrm{2ch\left(\frac{1+i}{\delta}a\right). ch\left(\frac{1-i}{\delta}a\right) = \left[ ch\left(\frac{2a}{\delta}\right) +\cos\left(\frac{2a}{\delta}\right) \right].}$$
et que de même:
$$\mathrm{2sh\left(\frac{1+i}{\delta}x\right). sh\left(\frac{1-i}{\delta}x\right) = \left[ ch\left(\frac{2x}{\delta}\right) -\cos\left(\frac{2x}{\delta}\right) \right].}$$
D’où l’expression de Q(x):
$$\mathrm{Q(x)=\frac{H_{0}^{2}}{\sigma\delta^{2}}\frac{{\displaystyle ch\frac{2 x}{\delta}-\cos\frac{2x}{\delta}}}{{\displaystyle ch\frac{2a}{\delta}+\cos\frac{2a}{\delta}}}.}$$

Lorsque la condition $ \mathrm{{\displaystyle \frac{a}{\delta}\ll 1}} $ est satisfaite, la condition $ \mathrm{{\displaystyle \frac{x}{\delta}\ll 1}} $ est satisfaite à fortiori. Remarquons qu’au second ordre en u:
$$\mathrm{\cos \left(u\right)=1-\frac{u^{2}}{2} +o\left(u^{2}\right)}$$

$$\mathrm{ch\left( u\right)=1+\frac{u^{2}}{2} +o\left(u^{2}\right)}$$
et que par conséquent:
ch(u) − cos(u) = u² + o(u²)
et
ch(u) + cos(u) = 2 + o(u²).
En reportant dans l’expression précédente, il vient donc:
$$\mathrm{Q(x) \approx \frac{2H_{0}^{2}}{\sigma}\frac{x^{2}}{\delta^{4}}.}$$

Lorsque la condition $ \mathrm{{\displaystyle \frac{a}{\delta}\gg 1}} $ est satisfaite, nous pouvons remarquer que:
$$\mathrm{ch\frac{2a}{\delta} \approx \exp \frac{2a}{\delta}\gg 1.}$$
Ceci nous permet d’éliminer le dénominateur et de ne garder que le résultat:

$$\mathrm{Q(x)=\frac{2H_{0}^{2}}{\sigma\delta^{2}} \exp\left(-\frac{2a}{\delta}\right) \left[ch\frac{2 x}{\delta}-\cos\frac{2x}{\delta}\right].}$$
Cette expression peut être encore simplifiée en remarquant que lorsque x n’est pas très grand devant δ, Q(x) prend une valeur très faible par rapport à celles obtenues pour x voisin de ±a et que par conséquent, négliger le terme en cosinus ne conduit pas en valeur absolue à des erreurs importantes, on peut donc écrire:

$$\mathrm{Q(x)=\frac{2H_{0}^{2}}{\sigma\delta^{2}} \exp\left(-\frac{2a}{\delta}\right). ch\left(\frac{2 x}{\delta}\right).}$$

La puissance surfacique totale dissipée est donnée par l’intégrale:
Q_tot = ∫_−a^aQ(x).dx
Il ne nous reste, après avoir sorti les constantes qu’à déterminer:
$$\mathrm{\int_{-a}^{a}\left[ch\frac{2 x}{\delta}-\cos\frac{2x}{\delta}\right]dx =\frac{\delta}{2} \left[sh\frac{2 x}{\delta}-\sin\frac{2x}{\delta}\right]_{-a}^{a} =\delta \left[sh\frac{2 a}{\delta}-\sin\frac{2a}{\delta}\right]}.$$
Ce qui nous conduit au résultat:
$$\mathrm{Q_{tot}=\frac{H_{0}^{2}}{\sigma\delta} \frac{{\displaystyle sh\frac{2 a}{\delta}-\sin\frac{2a}{\delta}}}{{\displaystyle ch\frac{2a}{\delta}+\cos\frac{2a}{\delta}}}.}$$
Ce résultat est bien de la forme:
$$\mathrm{Q_{tot}=\frac{H_{0}^{2}}{2\sigma a}g(\alpha)\:\text{avec}\: g(\alpha)=\alpha\frac{sh \alpha - \sin \alpha}{ch \alpha + \cos \alpha}\:;\:\alpha=\frac{2a}{\delta}} \label{Aeq15}$$

Application numérique:

Avec les valeurs numériques de l’énoncé: $ \mathrm{H_{0}={{10}^{5}}{A.m^{-1}}} $ ; $ \mathrm{\sigma={5.10^6}{\Omega^{-1}.m^{-1}}} $ ; $ \mathrm{\mu=10^2} $; $ \mathrm{f={50}{Hz}} $, nous obtenons:
$$\mathrm{\delta=\sqrt{\frac{2}{\sigma\mu_{0}\mu_{r}\omega}} ={3,18}{mm}}.$$
D’où les valeurs numériques:

a	α	g(α)	Qtot
$0,5 mm$	0,314	0,00162	$3,24 kW.m^{-2}$
$5 mm$	3,14	3,424	$685 kW.m^{-2}$
$50 mm$	31,4	31,4	$628 kW.m^{-2}$

Lorsque α ≫ 1, les fonctions hyperboliques sont en valeur absolues très grandes devant les fonctions trigonométriques et différent très peu l’une de l’autre, par conséquent:
$$\mathrm{Q_{tot}\approx \frac{H_{0}^{2}}{2\sigma a}\alpha=\frac{H_{0}^{2}}{\sigma \delta},}$$
la puissance dissipée est indépendante de l’épaisseur de la plaque métallique. En fait le chauffage se fait exclusivement dans les couches superficielles.
Si maintenant α ≪ 1, le développement limité au quatrième ordre en α de la fonction g(α) est:
$$\mathrm{g(\alpha)=\frac{\alpha^{4}}{6}+o(\alpha^{4})}.$$
Par conséquent:
$$\mathrm{Q_{tot} \approx \frac{H_{0}^{2}}{12\sigma a}\alpha^{4} =\frac{4}{3}\frac{H_{0}^{2}}{\sigma}\frac{a^{3}}{\delta^{4}}}.$$

Optimisation du chauffage:

Au vu des questions précédentes, il apparaît que le chauffage en volume est optimisé pour une épaisseur de peau δ voisine de la moitié de l’épaisseur du matériau à chauffer soit δ ≈ a, d’où le choix de la fréquence de travail:
$$\mathrm{a =\sqrt{\frac{2}{\mu\sigma\omega}}}.$$
Soit:
$$\mathrm{f=\frac{\omega}{2\pi}=\frac{2}{\pi\mu\sigma a^{2}}}.$$

ANALYSE THERMIQUE

Cas d’une plaque large devant la profondeur de pénétration a ≫ δ

La puissance totale dissipée dans l’ensemble de la plaque est donnée par [Aeq15]. Nous sommes ici dans le cas α ≫ 1 par conséquent les fonctions hyperboliques sont en valeur absolues très grandes devant les fonctions trigonométriques et différent très peu l’une de l’autre, par conséquent:
$$\mathrm{Q_{tot}\approx \frac{H_{0}^{2}}{2\sigma a}\alpha=\frac{H_{0}^{2}}{\sigma \delta},}$$
la puissance dissipée est indépendante de l’épaisseur de la plaque métallique. En fait le chauffage se fait exclusivement dans les couches superficielles.
Comme cette puissance est fournie symétriquement en x = a et en x = −a, le chauffage de la plaque peut se représenter par une densité de flux thermique entrant sur les faces x = −a et x = a de valeur :

$$\mathrm{\varphi_{0}=\frac{H_{0}^{2}}{2\sigma\delta}} \label{Beq4}$$

Au sein du milieu matériel, il n’y a pas de sources de chaleur, donc l’équation de la chaleur:
$$\mathrm{\rho C_{p}\frac{\partial T}{\partial t}-k\frac{\partial^{2}T}{\partial x^{2}}=p(x,t)} \label{Beq1}$$
se réduit en remarquant que p(x, t)=0 et que T = T_amb + θ où la température ambiante est une constante à:
$$\mathrm{\mathrm{\rho C_{p}\frac{\partial \theta}{\partial t}-k\frac{\partial^{2}\theta}{\partial x^{2}}=0}}.$$
En divisant par ρC_p, nous voyons apparaître la diffusivité thermique D d’où la relation:
$$\mathrm{\mathrm{\frac{\partial \theta}{\partial t}-D\frac{\partial^{2}\theta}{\partial x^{2}}=0}},$$
vérifiée au sein du matériau.
Le chauffage étant superficiel, et la chaleur ne pouvant s’accumuler aux interfaces, la loi de Fourier impose:
$$\mathrm{k\frac{\partial \theta}{\partial x}=\varphi_{0}\: \text{en} \:x=a}.$$
Les conditions aux limites imposées par le chauffage en x = a et x = −a sont les mêmes, le principe de Curie conduit à la recherche de solutions θ(x, t) fonctions paires de x. Comme la dérivée par rapport à x d’une fonction paire en x est une fonction impaire de x et qu’une fonction (continue) impaire est nécessairement nulle en x = 0: $ \mathrm{\displaystyle {\frac{\partial \theta}{\partial x}(0,t)=0}} $.
Initialement la barre est à la température ambiante donc θ(x, 0)=0.
Nous venons ainsi de justifier l’ensemble du modèle mathématique fourni par l’énoncé:

$$\mathrm{\frac{\partial \theta}{\partial t}-D\frac{\partial ^{2}\theta}{\partial x^{2}}=0} \label{Beq5}$$
où D est la diffusivité thermique $ \mathrm{{\displaystyle \left(D=\frac{k}{\rho C_{p}}\right)}} $, avec les conditions aux limites :
$$\mathrm{k\frac{\partial \theta}{\partial x}=\varphi_{0}\:\text{en}\:x=a\:\text{et}\:\frac{\partial \theta}{\partial x}=0\:\text{en}\:x=0} \label{Beq6}$$
et la condition initiale :
θ(x, 0)=0

En reportant la solution:
$$\mathrm{\theta_{0}(x,t) =\frac{\varphi_{0}a}{k}\left(\frac{Dt}{a^{2}}+\frac{x^{2}}{2a^{2}}\right)}$$
dans [Beq5], il vient:
$$\mathrm{\frac{\varphi_{0}a}{k}\frac{D}{a^{2}} -D\frac{\varphi_{0}a}{k}\frac{2a}{2a^{2}}=0}$$
et nous remarquons aisément que la dérivée
$$\mathrm{k\frac{\partial \theta}{\partial x}=2\frac{\varphi_{0}ax}{2a^{2}}=\varphi_{0}\frac{x}{a}}$$
est nulle pour x = 0 et vaut φ₀ pour x = a.
Par contre la condition initiale de [Beq7] n’est pas satisfaite.

Comme θ(x, t) et θ₀(x, t) sont deux solutions de l’équation [Beq5] qui est linéaire, leur différence θ^* est une solution de cette équation donc:
$$\mathrm{\frac{\partial \theta^{*}}{\partial t}-D\frac{\partial ^{2}\theta^{*}}{\partial x^{2}}=0} \label{Beq8}$$
en x = 0 et en x = a les deux fonctions ont la même dérivée, donc la dérivée de leur différence est nulle:

$$\mathrm{\frac{\partial\theta^{*}}{\partial x}=0\:\text{en}\:x=a\:\text{et}\:\frac{\partial \theta^{*}}{\partial x}=0\:\text{en}\: x=0.} \label{Beq9}$$
En ce qui concerne la condition initiale, θ(x, 0)=0 mais $ \mathrm{\theta_{0}(x,0) \not = 0} $ par conséquent en faisant la différence, il vient:

θ^*(x, 0)= − θ₀(x, 0)

Séparation des variables: 

En posant θ^*(x, t)=u(t).v(x) et en reportant dans l’équation de la chaleur réduite [Beq8], il vient:
$$\mathrm{v(x)\frac{du(t)}{dt}-Du(t)\frac{d^{2}v(x)}{dx^{2}}=0}.$$
Divisons membre à membre par la fonction u(t).v(x), il vient:
$$\mathrm{\frac{{\displaystyle \frac{du(t)}{dt}}}{Du(t)}= \frac{{\displaystyle \frac{d^{2}v(x)}{dx^{2}}}}{v(x)}}.$$
Supposons la date t choisie, alors nous constatons que le premier membre est nécessairement une constante et qu’il ne peut pas dépendre de x. De même si nous fixons x, nous remarquons que le second membre ne peut pas dépendre du temps. Comme ces deux membres sont toujours égaux, il ne peuvent dépendre ni de t ni de x sous peine de contradiction, par conséquent:
$$\mathrm{\frac{{\displaystyle \frac{du(t)}{dt}}}{Du(t)}= \frac{{\displaystyle \frac{d^{2}v(x)}{dx^{2}}}}{v(x)}=K} \label{Beq11}$$
où K est une constante réelle.

On pose K = −λ² où λ est réel. L’équation relative à v(x) s’écrit donc:
$$\mathrm{ \frac{d^{2}v(x)}{dx^{2}}+\lambda^{2}v(x)=0.}$$
Sa solution générale est de la forme:
v(x)=Acos(λx) + Bsin(λx).
La dérivée étant:
$$\mathrm{\frac{dv(x)}{dx}=\lambda\left[-A\sin\left(\lambda x\right) +B\cos\left(\lambda x\right)\right].}$$
Prenons en compte les conditions aux limites [Beq9], il vient:
B = 0 en x = 0  ⇒ B = 0
puis:
$$\mathrm{A\sin\left(\lambda a\right)=0\:\text{en}\:x=a\:\Longrightarrow \lambda=\frac{n\pi}{a}\:n \in \mathbb{Z}}.$$
Par conséquent:
$$\mathrm{v(x)=A\cos\left(n\pi\frac{x}{a}\right).} \label{Beq12}$$

Prenons maintenant en compte la deuxième équation différentielle:
$$\mathrm{\frac{du(t)}{dt}+\lambda^{2}Du(t)=0},$$
sa solution générale est:
u(t)=Cexp(−λ²Dt),
ce qui nous fournit une solution à variable séparables:
$$\mathrm{\theta^{*}_{n}(x,t)= A_{n}\exp\left(-D\frac{n^{2}\pi^{2}}{a^{2}}t\right) \cos\left(n\pi\frac{x}{a}\right).}$$
Toutes les fonctions de la forme précédente avec λ éventuellement nul sont solutions de l’équation linéaire [Beq8] et satisfont aux conditions aux limites [Beq9], il en est donc de même de leur superposition:
$$\mathrm{\theta^{*}(x,t)=\sum_{n \geq 0}^{}A_{n}\exp\left(-D\frac{n^{2}\pi^{2}}{a^{2}t}\right)\cos \left(n\pi\frac{ x}{a}\right)} \label{Beq13}$$
où les coefficients A_n sont des réels.

Ici l’énoncé original comporte une erreur, l’intégrale doit être nécessairement prise entre −a et +a pour que la fonction θ^*(x, 0) soit définie. Sinon, il faut faire un prolongement de cette fonction entre a et 2a respectant les symétries.
Pour $ \mathrm{n \not = 0} $, nous exploitons l’orthogonalité des fonctions cosinus, il vient:

$$\mathrm{\frac{1}{2a}\int_{-a}^{a}\cos\left(\frac{p\pi x}{a}\right) \cos\left(\frac{q\pi x}{a}\right)=\frac{1}{2}\delta_{pq}}$$
où p et q sont deux entiers relatifs et où δ_pq désigne le symbole de Kronecker, δ_pq = 0 si $ \mathrm{p\not = q} $ et δ_pq = 1 si p = q.
Par conséquent, en reprenant l’équation [Beq13] et en effectuant à l’instant t = 0, le calcul sur les deux membres, il vient:

$$\mathrm{\frac{1}{2a}\int_{-a}^{a}\theta^{*}(x,0)\cos \left(\frac{n\pi x}{a}\right)dx=\frac{1}{2}A_{n}} \label{Beq14}$$
Comme ici:
$$\mathrm{\theta^{*}_{0}(x,0)=-\theta_{0}(x,0) =-\frac{\varphi_{0}x^{2}}{2ka^{2}},}$$

$$\mathrm{A_{n}=-\frac{\varphi_{0}}{2ka^{2}}\int_{-a}^{a}x^{2}\cos \left(\frac{n\pi x}{a}\right)dx}.$$
Nous intégrons une première fois par parties en posant:
$$\mathrm{u=x^{2}\:\text{et}\:dv=\cos \left(\frac{n\pi x}{a}\right)dx}$$
d’où:
$$\mathrm{du=2x.dx\:\text{et}\:v=\frac{a}{n\pi}\sin \left(\frac{n\pi x}{a}\right)}.$$
Par conséquent dans un premier temps:
$$\mathrm{\int_{-a}^{a}x^{2}\cos \left(\frac{n\pi x}{a}\right)dx =\left[\frac{ax^{2}}{n\pi}\sin \left(\frac{n\pi x}{a}\right)\right]_{-a}^{a} +\int_{-a}^{a}-\frac{2a}{n\pi}\sin \left(\frac{n\pi x}{a}\right)dx}.$$

Le terme tout intégré est nul et il reste:
$$\mathrm{\int_{-a}^{a}x^{2}\cos \left(\frac{n\pi x}{a}\right)dx =-\frac{2a}{n\pi}\int_{-a}^{a}x\sin \left(\frac{n\pi x}{a}\right)dx}.$$
Nous effectuons une deuxième intégration par parties en posant:
$$\mathrm{u=x\:\text{et}\:dv=-\sin \left(\frac{n\pi x}{a}\right)dx}$$
d’où:
$$\mathrm{du=.dx\:\text{et}\:v=\frac{a}{n\pi}\cos \left(\frac{n\pi x}{a}\right)}.$$
Il vient donc:
$$\mathrm{-\int_{-a}^{a}x\sin \left(\frac{n\pi x}{a}\right)dx =\left[\frac{ax}{n\pi}\cos \left(\frac{n\pi x}{a}\right)\right]_{-a}^{a} -\int_{-a}^{a}\sin \left(\frac{n\pi x}{a}\right)dx. }$$
Cette fois-ci, c’est l’intégrale qui est nulle tandis que le terme entre crochets s’évalue facilement, il vient:
$$\mathrm{-\int_{-a}^{a}x\sin \left(\frac{n\pi x}{a}\right)dx =\frac{2a^{2}}{n\pi}\cos\left(n\pi\right) =\left(-1\right)^{n}\frac{2a^{2}}{n\pi}.}$$
En regroupant les résultats, il vient:
$$\mathrm{A_{n}=-\frac{\varphi_{0}}{2ka^{2}}.\frac{2a}{n\pi}. \left(-1\right)^{n}\frac{2a^{2}}{n\pi} =-\frac{2\varphi_{0}a}{k\pi^{2}} \frac{\left(-1\right)^{n}}{n^{2}}.}$$
Envisageons maintenant le cas particulier n = 0, il vient immédiatement:
$$\mathrm{\frac{1}{2a}\int_{-a}^{a}\theta^{*}(x,0)dx=A_{0}.}$$
Tenons compte de la forme initiale de θ^*(x, 0), il vient:
$$\mathrm{A_{0} =\frac{1}{2a}\int_{-a}^{a}-\frac{\varphi_{0}}{2ak}x^{2}dx}$$
soit:
$$\mathrm{A_{0}=-\frac{\varphi_{0}a}{6k}.}$$
Nous sommes alors en mesure d’écrire le développement complet de θ(x, t):
$$\mathrm{\theta(x,t)=\frac{\varphi_{0}a}{k}\left\{ \frac{Dt}{a^{2}}+\frac{x^{2}}{2a^{2}}-\frac{1}{6}-\frac{2}{\pi^{2}}\sum_{n>0} \frac{\left(-1\right)^{n}}{n^{2}} \exp\left(-D\frac{n^{2}\pi^{2}}{a^{2}}t\right). \cos\left(n\pi\frac{x}{a}\right)\right\}}.$$

La dépendance temporelle du régime transitoire est contenue dans les termes $ {\displaystyle \mathrm{\exp\left(-D\frac{n^{2}\pi^{2}}{a^{2}}t\right)}} $, celui que décroît le moins rapidement correspond à n = 1 et la constante de temps associée est:
$$\mathrm{\tau_{1}=\frac{a^{2}}{D\pi^{2}}}.$$
Il vient numériquement $ \mathrm{\tau={22,5}{s}} $, l’évolution temporelle de la température est donc voisine de θ₀(x, t) au bout d’environ une minute.

La température ambiante n’étant pas fournie, nous prendrons $ \mathrm{T_{amb}={300}{K}} $, le problème à résoudre consiste donc à trouver la date à laquelle $ \mathrm{\theta_{0}(a,t)={700}{K}=\theta_{1}} $². L’équation à résoudre est donc:
$$\mathrm{\theta_{1} =\frac{\varphi_{0}a}{k}\left(\frac{Dt}{a^{2}}+\frac{1}{2}\right)}$$
d’où:
$$\mathrm{t =\frac{a^{2}}{D}\left(\frac{k\theta_{1}} {\varphi_{0}a}-\frac{1}{2}\right)}.$$
Nous avons déjà déterminé $ \mathrm{\varphi_{0}={314}{kW.m^{-2}}} $, $ {\displaystyle \mathrm{D=\frac{k}{\rho C_{p}}}={1,125.{10}^{-5}}{s.m^{-2}}} $, d’où:
$$\mathrm{t=222,2.\left(\frac{45\times 700}{314.10^{3}\times 0,05}-\frac{1}{2}\right)={335}{s}\approx \ 5mn30s}.$$
Ce temps de chauffage est effectivement très supérieur à la durée typique du régime transitoire. Ce qui légitime l’approximation effectuée (au terme constant du développement en série de Fourier près!)
L’écart de température entre le bord et le centre de la plaque est donné par:
$$\mathrm{\theta_{0}(a,t)-\theta_{0}(0,t)=\frac{\varphi_{0}a}{2k} ={174}{K}}.$$

Cas général:

On cherche à résoudre l’équation:
$$\mathrm{\rho C_{p}\frac{\partial \theta}{\partial t}-k\frac{\partial^{2}\theta}{\partial x^{2}}=Q(x)} \label{Beq15}$$
lorsque Q(x) est donnée par :

$$\mathrm{Q(x)=\frac{H_{0}^{2}}{\sigma \delta^{2}}\frac{{\displaystyle ch\frac{2x}{\delta}-\cos\frac{2x}{\delta}}}{{\displaystyle ch\frac{2a}{\delta}+\cos\frac{2a}{\delta}}}}$$
Les conditions aux limites sont données par :
$$\mathrm{k\frac{\partial \theta}{\partial x}+h\theta=0 \:\text{en}\:x=a} \label{Beq16}$$
où h est une constante traduisant la convection thermique ;
$$\mathrm{\frac{\partial \theta}{\partial x}=0\:\text{en}\:x=0} \label{Beq17}$$

Régime permanent:

On suppose que $ \mathrm{{\displaystyle \frac{\partial \theta}{\partial t}(x,t)=0}} $. On note θ_∞(x) la solution correspondante.

B.2.1.1�) L’équation de la chaleur [Beq15] se réduit à:

$$\mathrm{\frac{d^{2}\theta_{\infty}(x)}{d x^{2}} =-\frac{1}{k}Q(x)=-\frac{H_{0}^{2}}{k\sigma \delta^{2}}\frac{{\displaystyle ch\frac{2x}{\delta}-\cos\frac{2x}{\delta}}}{{\displaystyle ch\frac{2a}{\delta}+\cos\frac{2a}{\delta}}}}$$
Une première intégration par rapport à x fournit l’expression:
$$\mathrm{\frac{d\theta_{\infty}}{dx}(x)= C-\frac{H_{0}^{2}}{2k\sigma \delta}\frac{{\displaystyle sh\frac{2x}{\delta}-\sin\frac{2x}{\delta}}}{{\displaystyle ch\frac{2a}{\delta}+\cos\frac{2a}{\delta}}}},$$
la constante C se détermine en appliquant la condition [Beq17], il vient immédiatement C = 0.
Une seconde intégration par rapport à x fournit:
$$\mathrm{\theta_{\infty}(x)=D-\frac{H_{0}^{2}}{4\sigma k}\frac{{\displaystyle ch\frac{2x}{\delta}+\cos\frac{2x}{\delta}}}{{\displaystyle ch\frac{2a}{\delta}+\cos\frac{2a}{\delta}}}}.$$
La constante d’intégration D se détermine en reportant ce résultat dans la condition [Beq16], il vient:
$$\mathrm{-k\frac{H_{0}^{2}}{2k\sigma \delta}\frac{{\displaystyle sh\frac{2a}{\delta}-\sin\frac{2a}{\delta}}}{{\displaystyle ch\frac{2a}{\delta}+\cos\frac{2a}{\delta}}}+ h\left\{D-\frac{H_{0}^{2}}{4\sigma k}\frac{{\displaystyle ch\frac{2a}{\delta}+\cos\frac{2a}{\delta}}}{{\displaystyle ch\frac{2a}{\delta}+\cos\frac{2a}{\delta}}}\right\}=0}.$$
Soit:
$$\mathrm{D=\frac{H_{0}^{2}}{4\sigma k}+\frac{H_{0}^{2}}{2\sigma \delta h}\frac{{\displaystyle sh\frac{2a}{\delta}-\sin\frac{2a}{\delta}}}{{\displaystyle ch\frac{2a}{\delta}+\cos\frac{2a}{\delta}}}}$$
il nous suffit alors de remplacer la constante par sa valeur dans l’expression de θ_∞(x) pour obtenir le résultat donné par l’énoncé:
$$\mathrm{\theta_{\infty}(x)=\frac{H_{0}^{2}}{k\sigma}\left[\frac{1}{4} \left(1-\frac{{\displaystyle ch\frac{2x}{\delta}+\cos \frac{2x}{\delta}}}{\mathrm{ch \alpha +\cos \alpha}}\right) +\frac{k}{2\delta h}\left(\frac{{\displaystyle sh \alpha - \sin \alpha}}{{\displaystyle ch \alpha}+\cos \alpha}\right)\right]} \label{Beq18}$$
où $ \mathrm{{\displaystyle \alpha=\frac{2a}{\delta}}} $.
B.2.1.2�) Lorsque α → 0, il est clair que $ \mathrm{{\displaystyle \frac{x}{\delta}}} $ tend également vers zéro.
On constate immédiatement que:
lim_α → 0θ_∞(x)=0.
L’interprétation de ce résultat vient du fait que dans ces conditions, on a également Q(x)→0. La température ne change pas car le chauffage de la plaque n’est pas efficace.

B.2.1.3�) Lorsque α → ∞, les fonctions hyperboliques peuvent être remplacées par leur équivalent exponentiel tandis que les fonctions trigonométriques restent comprises entre −1 et +1, on peut donc écrire:

$$\mathrm{\theta_{\infty}(x) \approx \frac{H_{0}^{2}}{2\sigma \delta h}+\frac{H_{0}^{2}}{4k\sigma}\left[1-2\exp\left(-\alpha\right) ch\left(\frac{2x}{\delta}\right)\right]}.$$
Remarquons que ce deuxième terme est nul pour x = ±a et qu’il est pratiquement constant dès que |x| < a − 3δ.
Le premier terme revient à considérer que la température superficielle est telle que toute la puissance reçue de la part du champ électromagnétique est évacuée vers l’extérieur par les transferts convectifs, le second terme montre que, sauf au voisinage immédiat de la surface, la température tend à s’homogénéiser à l’intérieur du matériau.

Régime transitoire

B.2.2.1�) On effectue le changement de fonction inconnue :

θ^*(x, t)=θ(x, t)−θ_∞(x)
Les fonctions θ(x, t) et θ_∞(x) étant solutions de l’équation linéaire:

$$\mathrm{\rho C_{p}\frac{\partial \theta}{\partial t}-k\frac{\partial^{2}\theta}{\partial x^{2}}=Q(x)},$$

$$\mathrm{\rho C_{p}\frac{\partial \theta\infty}{\partial t}-k\frac{\partial^{2}\theta_{\infty}}{\partial x^{2}}=Q(x)},$$
la différence membre à membre fournit:
$$\mathrm{\frac{\partial \theta^{*}}{\partial t}-D\frac{\partial ^{2}\theta^{*}}{\partial x^{2}}=0\:\:\:\:\:0<x<a} \label{Beq20}$$
De même, en x = a:
$$\mathrm{k\frac{\partial \theta}{\partial x}+h\theta=0 }$$

$$\mathrm{k\frac{\partial \theta_{\infty}}{\partial x}+h\theta_{\infty}=0 }$$
d’où par différence:
$$\mathrm{k\frac{\partial \theta^{*}}{\partial x}+h\theta^{*}=0\:\:\text{en}\:x=a} \label{Beq21}$$
Le même argument permet de justifier la condition:
$$\mathrm{\frac{\partial \theta^{*}}{\partial x}=0\:\:\text{en}\:x=0} \label{Beq22}$$
La condition initiale :
θ^*(x, 0)= − θ_∞(x)
provient de l’absence d’échauffement initial de la barre.
B.2.2.2�) On envisage une résolution du problème défini en B.2.2.1�) par variables séparées.
On pose θ^*(x, t)=u(t).v(x). L’argumentation est en tous points identique à celle développée en [B.1.5.]:
$$\mathrm{\frac{{\displaystyle \frac{du(t)}{dt}}}{Du(t)}= \frac{{\displaystyle \frac{d^{2}v(x)}{dx^{2}}}}{v(x)}=K} \label{Beq24}$$
où K est une constante réelle.

B.2.2.3�) On pose K = −λ² où λ est réel.
L’équation relative à v(x) s’écrit donc:
$$\mathrm{ \frac{d^{2}v(x)}{dx^{2}}+\lambda^{2}v(x)=0.}$$
Sa solution générale est de la forme:
v(x)=Acos(λx) + Bsin(λx).
La dérivée étant:
$$\mathrm{\frac{dv(x)}{dx}=\lambda\left[-A\sin\left(\lambda x\right) +B\cos\left(\lambda x\right)\right].}$$
Prenons en compte la conditions aux limites [Beq22], il vient:
B = 0 en x = 0  ⇒ B = 0
puis, en faisant appel à la condition [Beq21], il vient:
$$\mathrm{-k\lambda A\sin\left(\lambda a\right)+hA\cos\left(\lambda a\right)=0\: \text{en}\:x=a\:\Longrightarrow \tan\left(\lambda a\right)=\frac{h}{k\lambda}}.$$
Nous identifions ainsi l’équation de l’énoncé
$$\mathrm{\tan\left(\lambda a\right)=\frac{h}{k\lambda}.} \label{Beq25}$$
B.2.2.4�) Lorsque λ_n ≫ 1, nous remarquons que le second membre tend vers zéro, par conséquent λa est proche d’un zéro de la fonction tangente, le zéro d’ordre n étant nπ, on peut donc poser λa ≈ nπ, il vient donc:
$$\mathrm{\lambda_{n}\approx n\frac{\pi}{a}}.$$
B.2.2.5�) Prenons maintenant en compte la deuxième équation différentielle:
$$\mathrm{\frac{du(t)}{dt}+\lambda_{n}^{2}Du(t)=0},$$
sa solution générale est:
u(t)=Cexp(−λ_n²Dt),
ce qui nous fournit une solution à variable séparables:
$$\mathrm{\theta^{*}_{n}(x,t)= A_{n}\exp\left(-D\lambda_{n}^{2}t\right) \cos\left(n\pi\frac{x}{a}\right).}$$
La solution θ^*(x, t) peut s’écrire :

$$\mathrm{\theta^{*}(x,t)=\sum_{n\geq 0}^{}A_{n}\exp\left(-D\lambda_{n}^{2}t\right) \cos \left(\lambda_{n}x\right)} \label{Beq26}$$
où les coefficients A_n sont des réels car toutes les solutions à variables séparées de l’équation linéaire [Beq20] que nous avons obtenues satisfont aux conditions aux limites [Beq21] et [Beq22].
B.2.2.6�) L’ expression générale de θ(x, t) s’obtient en calculant la somme:
θ(x, t)=θ^*(x, t)+θ_∞(x).

$$\begin{gathered} \mathrm{\theta(x,t)= \frac{H_{0}^{2}}{k\sigma}\left[\frac{1}{4} \left(1-\frac{{\displaystyle ch\frac{2x}{\delta}+\cos \frac{2x}{\delta}}}{\mathrm{ch \alpha +\cos \alpha}}\right) +\frac{k}{2\delta h}\left(\frac{{\displaystyle sh \alpha - \sin \alpha}}{{\displaystyle ch \alpha}+\cos \alpha}\right)\right]} \\ \mathrm{+\sum_{n\geq 0}^{}A_{n}\exp\left(-D\lambda_{n}^{2}t\right) \cos \left(\lambda_{n}x\right).} \end{gathered}$$
Il est hors de question de préciser davantage le développement car le calcul explicite des coefficients est très compliqué, non seulement à cause de la forme de θ_∞(x) mais également parce que le développement n’est pas un développement en série de Fourier.
B.2.2.7�) Évaluation du temps de montée en température:

Nous nous contentons d’évaluer λ₀ qui permet d’obtenir la constante de temps de la composante du régime transitoire ayant la décroissance la plus lente. Il nous faut donc résoudre l’équation [Beq25], cette résolution peut se faire graphiquement en traçant les courbes représentatives des deux membres et en cherchant leur intersection. Il vient $ \mathrm{\lambda_{0}={1,49}{m^{-1}}} $ pour $ \mathrm{h={5}{W.m^{-2}.K^{-1}}} $ et $ \mathrm{\lambda_{0}={13,7}{m^{-1}}} $ pour $ \mathrm{h={500}{W.m^{-2}.K^{-1}}} $.
Ce qui nous fournit les constantes de temps:
$$\mathrm{\tau_{0}=\frac{1}{D\lambda_{0}^{2}}=\frac{\rho C_{p}}{k\lambda_{0}^{2}}\bullet ,}$$
de valeurs respectives $ \mathrm{{40.10^{3}}{s} \approx{11}{h}} $ pour $ \mathrm{h={5}{W.m^{-2}.K^{-1}}} $ et $ \mathrm{\tau_{0}={473}{s}\approx 8 mn} $ pour $ \mathrm{h={500}{W.m^{-2}.K^{-1}}} $.

B.2.2.8�) Évaluation d’une température:
Dans les conditions étudiées, la température est conditionnée par le régime transitoire. Nous ne retenons que le terme du premier ordre donc:
θ(x, t)≈θ_∞(x)+A₀exp(−Dλ₀²t)cos(λ₀x).
Il nous faut donc évaluer A₀. Dans le temps qui nous est imparti nous ne pouvons que rechercher l’approximation la plus simple possible en remarquant qu’au centre de la barre θ(0, 0)=0, ce qui fournit A₀ = θ_∞(0) d’où:
θ(0, t)≈θ_∞(0)[1−exp(−Dλ₀²t)].
En exprimant θ_∞ en fonction des données, il vient:
$$\mathrm{\theta(0,t)={1610}{K}},$$
ce qui est une température limite tout à fait raisonnable compte tenu de l’objectif fixé. D’où la valeur de la température au centre de la barre au bout de trois minutes $ \mathrm{\theta(0,180)={7,2}{K}} $ alors que selon le premier modèle, nous aurions eu:
$$\mathrm{\theta(0,180) \approx \frac{\varphi_{0}Dt}{ka} =\frac{H_{0}^{2}}{2\sigma \delta}\frac{k}{\rho C_{p}}\frac{t}{ka} =\frac{H_{0}^{2}}{4\sigma a^{2}}\frac{t}{\rho C_{p}} ={13,5}{K}}.$$
Les pertes thermiques rendent donc le début du chauffage deux fois plus lent, ce phénomène ne peut que s’aggraver à mesure que la température superficielle augmente.
Le résultat ne peut pas se comparer valablement à celui du [B.1.10.] car la valeur de α n’est pas la même! (Au [B.1.10.], α = 15.

ANALYSE MÉCANIQUE

L’extrémité de la barre d’abscisse x = 0 sera considérée comme fixe par rapport au repère absolu.

Données du problème:

$$\mathrm{\frac{\partial N(x,t)}{\partial x}-\frac{\partial^{2}u(x,t)}{\partial t^{2}}=0} \label{Ceq1}$$

$$\mathrm{N(x,t)=\Lambda\left(\frac{\partial u(x,t)}{\partial x}-\lambda \theta(x,t)\right)} \label{Ceq2}$$
La première équation traduit, en projection sur l’axe $ \mathrm{{\overrightarrow{\vphantom{(^{1}}\mathrm{x}}}} $, le principe fondamental de la dynamique.

Étude de vibrations:

Dans cette partie, on considère que la variation de température est nulle θ(x, t)=0 ; il n’y << donc pas d’effet thermique.

Comme dans cette partie il n’y a pas d’effet de température, l’équation [Ceq2] se réduit à:
$$\mathrm{N(x,t)=\Lambda\frac{\partial u(x,t)}{\partial x},}$$
Il suffit de reporter ce résultat dans l’équation [Ceq1] pour obtenir:
$$\mathrm{\frac{\partial ^{2}u}{\partial x^{2}}-\frac{p}{\Lambda}\frac{\partial^{2}u}{\partial t^{2}}=0.} \label{Ceq3}$$

Considérons la masse m_i, l’allongement du ressort situé à droite de m_i est u_i + 1 − u_i et il exerce sur cette masse une force qui en projection sur $ \mathrm{{\overrightarrow{\vphantom{(^{1}}\mathrm{x}}}} $ a pour valeur:
f₊ = k(u_i + 1−u_i),
de même, l’allongement du ressort situé à gauche de m_i est u_i − u_i − 1, il exerce cette masse une force qui en projection sur $ \mathrm{{\overrightarrow{\vphantom{(^{1}}\mathrm{x}}}} $ a pour valeur:
f₋ = −k(u_i−u_i − 1),
dans le référentiel galiléen d’étude, la loi fondamentale de la dynamique newtonienne s’écrit:
$$\mathrm{m_{i}\frac{d^{2}u_{i}}{dt^{2}} =k\left[u_{i+1}+u_{i-1}-2u_{i}\right].} \label{Ceq4}$$

Considérons maintenant les u_i comme les valeurs aux points d’abscisses successives (i−1)l d’une fonction u(x, t), un développement limité au second ordre de cette fonction est d’après la formule de Taylor:
$$\mathrm{u_{i+1}=u_{i}+l\frac{\partial u}{\partial x}\left(x_{i},t\right) +\frac{l^{2}}{2}\frac{\partial^{2}u}{\partial x^{2}} \left(x_{i},t\right)+o(l^{2}).} \label{Ceq5}$$

De même:
$$\mathrm{u_{i-1}=u_{i}-l\frac{\partial u}{\partial x}\left(x_{i},t\right) +\frac{l^{2}}{2}\frac{\partial^{2}u}{\partial x^{2}} \left(x_{i},t\right)+o(l^{2}).} \label{Ceq6}$$

En reportant les équations [Ceq6] et [Ceq5] dans [Ceq4], il vient immédiatement:
$$\mathrm{m_{i}\frac{\partial^{2}u}{\partial t^{2}}=k\frac{\partial^{2}u}{\partial x^{2}}+o(l^{2})} \label{Ceq7}$$
Comme p est la masse linéique de la barre, nous identifions immédiatement $ {\displaystyle \mathrm{p=\frac{m_{i}}{l}}} $ soit:
m_i = p.L
En remarquant que l’équation [Ceq7] peut se mettre sous la forme:
$$\mathrm{m\frac{\partial^{2}u}{\partial x^{2}} -\frac{m}{k}\frac{\partial^{2}u}{\partial t^{2}}=0,}$$
nous identifions:
$$\mathrm{\frac{m_{i}}{k}=\frac{p}{\Lambda}}$$
d’où:
$$\mathrm{k=m_{i}\frac{\Lambda}{p}=\Lambda L}.$$

Séparation des variables:

En posant u(x, t)=X(x).f(t) et en reportant dans l’équation de propagation [Ceq3], il vient:
$$\mathrm{f(t)\frac{d^{2}X(x)}{dx^{2}} -\frac{p}{\Lambda}X(x)\frac{d^{2}f(t)}{dt^{2}}=0}.$$
Divisons membre à membre par la fonction X(x).f(t), il vient:
$$\mathrm{\frac{1}{X(x)}\frac{d^{2}X(x)}{dx^{2}} =\frac{p}{\Lambda}\frac{1}{f(t)}\frac{d^{2}f(t)}{dt^{2}} }$$
Supposons la date t choisie, alors nous constatons que le second membre est nécessairement une constante et qu’il ne peut pas dépendre de x. De même si nous fixons x, nous remarquons que le second membre ne peut pas dépendre du temps. Comme ces deux membres sont toujours égaux, il ne peuvent dépendre ni de t ni de x sous peine de contradiction, par conséquent:
$$\mathrm{\frac{1}{X(x)}\frac{d^{2}X(x)}{dx^{2}} =\frac{p}{\Lambda}\frac{1}{f(t)}\frac{d^{2}f(t)}{dt^{2}} =K\:\text{o{\`u}}\:K\:\text{est une constante.}}$$

On admet que K < 0 et on pose K = −μ² où μ est réel.
La fonction X(x) est par conséquent solution l’équation différentielle:
$$\mathrm{\frac{d^{2}X(x)}{dx^{2}}+\mu^{2}X(x)=0,}$$
de solution générale:
X(x)=Acos(μx) + Bsin(μx).
En x = 0, la barre est fixée, par conséquent X(0)=0 donc A = 0.
A l’extrémité libre de la barre, la force exercée sur celle-ci est nulle, il vient donc:
$$\mathrm{N(L,t)=\Lambda f(t)\frac{dX}{dt}=0},$$
ce qui nous conduit à l’équation:
sin(μ.L)=0,
de solution:
$$\mathrm{\mu_{n}=n\frac{\pi}{L}\:\text{o{\`u}}\:n \in \mathbb{Z}}.$$

La solution générale de l’équation différentielle relative à la fonction f(t):
$$\mathrm{\frac{p}{\Lambda}\frac{d^{2}f(t)}{dt^{2}}+\mu_{n}^{2}f(t)=0},$$
est de la forme:
f(x)=A_ncos(ω_nt) + B_nsin(ω_nt).
D’où une solution à variables séparées de la forme:
u(x, t)=sin(μ_nx)[A_ncos(ω_nt)+B_nsin(ω_nt)],
il n’y a ici que deux constantes indépendantes, le produit d’une constante arbitraire par une constante arbitraire étant lui même une constante arbitraire.
Comme l’équation [Ceq3] est une équation aux dérivées partielles linéaire, toute combinaison linéaire arbitraire de solutions est une solution, c’est donc le cas de:
$$\mathrm{u(x,t)=\sum_{n \geq 0}^{}\sin \left(\mu_{n}x\right).\left[A_{n}\cos\left(\omega_{n}t\right) +B_{n}\sin\left(\omega_{n}t\right)\right]}.$$
Cette solution satisfait de manière évidente aux conditions aux limites u(0, t)=0 et $ \mathrm{{\displaystyle\frac{\partial u}{\partial x}(a,t)=0}} $.

Au cours de l’établissement de la seconde équation différentielle, nous avons en fait posé:
$$\mathrm{\omega_{n}^{2}=\frac{\Lambda}{p}\mu_{n}^{2}},$$
par conséquent:
$$\mathrm{\omega_{n}=\sqrt{\frac{\Lambda}{p}}\mu_{n} =n \sqrt{\frac{\Lambda}{p}}\frac{\pi}{L}}.$$

L’expression finale de u(x, t) est donc:
$$\mathrm{u(x,t)=\sum_{n \geq 0}^{}\sin \left(n\pi\frac{x}{L}\right).\left[A_{n} \cos\left(n \sqrt{\frac{\Lambda}{p}}\frac{\pi}{L}t\right) +B_{n}\sin\left(n \sqrt{\frac{\Lambda}{p}}\frac{\pi}{L}t\right)\right]}.$$
Cette expression est celle qui traduit les vibrations libres de la barre en traction/compression.

Détermination préliminaire des efforts internes:

On se place dans le cas où il n’y a pas d’élévation de température et où les accélérations sont nulles.
L’équation [Ceq1] se réduit à:
$$\mathrm{ \frac{\partial N(x,t)}{\partial x}=0} \label{Ceq8}$$
par conséquent:
N(x, t)=f(θ)
et comme il n’y a pas de variation de température:
N = Cste.

La résultante générale des forces extérieures appliquées à la barre est nulle, celle-ci est immobile dans le référentiel galiléen d’étude, elle est en équilibre.
La loi de l’action et de la réaction appliquée à l’élément terminal de la barre montre que N(x, t)=F.

Étude thermique préliminaire

La barre n’étant soumise à aucun effort, l’équation [Ceq2] se réduit à:
$$\mathrm{\frac{\partial u(x,t)}{\partial x}=\lambda \theta(x,t)} \label{Ceq9}$$
(Nous aurions aussi pu utiliser des dérivées droites car les phénomènes sont indépendants du temps).

L’équation de la chaleur s’écrit de manière générale [Beq1]
$$\mathrm{\rho C_{p}\frac{\partial T}{\partial t}-k\frac{\partial^{2}T}{\partial x^{2}}=0}$$
en l’absence de sources interne de chaleur³
Le phénomène étant indépendant du temps, T ne dépend que de x, il vient donc, en remplaçant d’ailleurs T par T_amb + θ(x):
$$\mathrm{\frac{d^{2}\theta}{dx^{2}}=0},$$
d’où:
θ(x)=α.x + β
et comme θ(0)=A, il vient β = A.
En reportant la condition θ(L)=B dans l’équation ainsi obtenue, il vient:
B = A + αL
d’où la valeur du second coefficient:
$$\mathrm{\alpha=\frac{B-A}{L}},$$
par conséquent:
$$\mathrm{\theta(x)=A+\left(B-A\right)\frac{x}{L}.}$$

Étude thermomécanique:

Dans cette partie, on se place en régime thermique permanent et on considère que les accélérations sont nulles.

Le régime thermique est permanent donc θ ne dépend que de x, comme la barre est libre en x = L, il n’y a pas d’effort interne par conséquent:
$$\mathrm{N=0\:\text{et}\: \frac{\partial u(x,t)}{\partial x}=\lambda \theta(x,t)} \label{Ceq10}$$

Nous avons déjà montré que N(x, t)=0, l’intégration de la seconde équation
$$\mathrm{\frac{du}{dx}=\lambda \left[A+ \left(B-A\right)\frac{x}{L}\right]}$$
s’intègre aisément en:
$$\mathrm{u=C+\lambda \left[A.x+ \left(B-A\right)\frac{x^{2}}{2L}\right]}.$$
En tenant compte de la condition aux limites u(0)=0 il vient:
$$\mathrm{u=\lambda \left[A.x+ \left(B-A\right)\frac{x^{2}}{2L}\right]}.$$

L’extrémité étant libre l’effort interne reste nul La dilatation totale de la barre est:
$$\mathrm{u(L)=\lambda\frac{A+B}{2}L={3,75}{cm}}.$$

Les équations [Ceq1] et [Ceq2] se réduisent à:
$$\mathrm{\frac{dN}{dx}=0\:\text{et}\:N=\Lambda\left(\frac{du}{dx}-\lambda \theta\right)}.$$

La première équation nous montre que N(x, t) est une constante, la seconde équation se réduit alors à:
$$\mathrm{\frac{du}{dx}=\frac{N}{\Lambda}+\lambda \theta =\frac{N}{\Lambda}+\lambda \left[A+ \left(B-A\right)\frac{x}{L}\right]}.$$
L’intégration en x est simple, il vient:
$$\mathrm{u(x)=\alpha +\frac{N}{\Lambda}x+\lambda A x+\lambda \frac{B-A}{L}\frac{x^{2}}{2}}.$$
La condition aux limites u(0, t)=0 implique α = 0 et la seconde condition aux limites est maintenant u(L, t)=0 d’où l’équation:
$$\mathrm{0= +\frac{N}{\Lambda}L+\lambda A L+\lambda \frac{B-A}{L}\frac{L^{2}}{2}}.$$
d’où nous tirons:
$$\mathrm{N=-\lambda \Lambda\frac{A+B}{2}}$$
et
$$\mathrm{u(x)=\lambda\frac{B-A}{2}x\left(\frac{x}{L}-1\right)}.$$

L’effort interne exercé sur la barre serait calculable si nous disposions de Λ !
Le déplacement maximal, obtenu pour $ {\displaystyle \mathrm{x=\frac{L}{2}}} $ a pour valeur
$$\mathrm{u_{max}=-\lambda\frac{B-A}{8}L ={9,4}{mm}}.$$

Le profil de dilatation obtenu par résolution du système d’équations [Ceq10] correspond à un profil parabolique pour lequel il y a l’annulation de u en x = 0 et annulation de la dérivée $ \mathrm{{\displaystyle \frac{du}{dx}}} $ en x = L, tandis que dans le cas Ceq11, les conditions aux limites imposent l’annulation de u(x) en x = 0 et x = L.

---

1. Nous rajoutons ces hypothèses non mentionnées explicitement par l’énoncé↩
2. On peut aussi interpréter l’énoncé en supposant que représente l’augmentation de la température superficielle↩
3. Sous réserve que la masse volumique, la chaleur massique et la conductivité thermique soient des constantes indépendantes de la température et de la position. Nous négligeons ici les faibles variations de masse volumique résultant des phénomènes de dilatation .↩