Concours Physique Concours Commun M et P’ Physique I 1994 (Énoncé)

A 94 PHYS. I - M, P’
ÉCOLE NATIONALE DES PONTS ET CHAUSSÉES,
ÉCOLES NATIONALES SUPÉRIEURES DE L'AÉRONAUTIQUE ET DE L'ESPACE,
DE TECHNIQUES AVANCÉES, DES TÉLÉCOMMUNICATIONS,
DES MINES DE PARIS, DES MINES DE SAINT-ÉTIENNE, DES MINES DE NANCY,
DES TÉLÉCOMMUNICATIONS DE BRETAGNE,
ÉCOLE POLYTECHNIQUE (OPTION T.A.)
CONCOURS D'ADMISSION 1994
PHYSIQUE
PREMIÈRE ÉPREUVE
OPTIONS M et P'
(Durée de l'épreuve : 3 heures)
Les candidats sont priés de mentionner de façon apparente sur la première page de la co­pie : PHYSIQUE I.
L'énoncé de cette épreuve, commune aux candidats des options M et P', comporte 6 pages.
L’épreuve est constituée de deux problèmes indépendants entre eux et que l’on pourra aborder dans l’ordre qu’on voudra.
On étudie dans ce problème le fonctionnement et la mise en œuvre de circuits présentant le phé­nomène de résistance différentielle négative, c’est-à-dire tels que le rapport $r = \frac{\Delta e}{\Delta i}$ des pe­tites variations de tension et de courant autour d’un point de repos soit négatif. Les amplifica­teurs opérationnels AO (fig.1a) intervenant dans les divers montages auront des cou­rants d’en­trée ${i_1}$ et ${i_2}$ nuls et leur impédance d’entrée sera considérée comme infinie.

fig.1 a : Notations pour AO fig. 1b : Circuit pouvant exhiber $r = \frac{\Delta e}{\Delta i}<0$
Première partie : Réalisation de circuits d’impédance différentielle négative
On considère d’abord que le gain des amplificateurs est infini ; dans ces conditions, le régime li­néaire de fonctionnement se caractérise par ${V_1} = {V_2}$ ; autrement, la tension de sor­tie est
${V_s} = signe\left( {{V_2} - {V_1}} \right) \times E$ (régime dit de saturation,$E = 15V$ = tension de satura­tion ).

I -1) Déterminer la relation $i\left( e \right)$ dans le circuit de la figure 1b, d’abord en régime linéaire, puis en régime de saturation. Pour quelles inégalités portant sur $e$ ce dernier régime est-il possible (distinguer les cas ${V_s} = \pm E$) ?
I -2) Représenter le graphe complet de la relation $i\left( e \right)$ lorsque ${R_0} < R$, en précisant les points particuliers et les différents domaines de fonctionnement.
On considère maintenant que la tension de sortie des amplificateurs opérationnels s’exprime en fonction de la tension d’entrée par ${V_s} = A\left( {{V_2} - {V_1}} \right)$, où $A$ est un nombre réel très grand de­vant 1. Les relations entre tensions et courants dans le circuit représenté sur la figure 2a (redessinée en 2b) sont linéaires et peuvent donc s’écrire, avec les conventions habituelles re­latives aux gran­deurs complexes décrivant le régime harmonique : $\begin{array}{l}\underline {{I_1}} = \underline {{Y_{11}}} \,\underline {{V_1}} + \underline {{Y_{12}}} \,\underline {{V_2}} \\\underline {{I_2}} = \underline {{Y_{21}}} \,\underline {{V_1}} + \underline {{Y_{22}}} \,\underline {{V_2}} \end{array}$, soit, en notation matricielle : $\left[ {\begin{array}{*{20}{c}}{\underline {{I_1}} }\\{\underline {{I_2}} }\end{array}} \right] = \left[ {\underline Y } \right]\,\left[ {\begin{array}{*{20}{c}}{\underline {{V_1}} }\\{\underline {{V_2}} }\end{array}} \right]$. La matrice $\left[ {\underline Y } \right]$ ainsi intro­duite s’appelle matrice ad­mit­tance.

fig. 2a : Un circuit à AO fig. 2b : Circuit 2a, présenté comme un quadripôle
Remarquer que les courants sont comptés positivement quand ils entrent dans le qua­dri­pôle.
I-3) Calculer la matrice$\left[ {\underline Y } \right]$ relative au circuit considéré.
I-4) Quelle est, dans le cas général, la matrice $\left[ {\underline Y } \right]$ relative à deux quadripôles de matrices admittances res­pectives $\left[ {\underline {Y\,'} } \right]$ et $\left[ {\underline {Y\,''} } \right]$, montés en pa­rallèle (c’est-à-dire en reliant ensemble leurs bornes homo­logues) ?
I-5) Calculer, pour le circuit de la fig. 2, la matrice $\left[ {\underline M } \right]$ définie par $\left[ {\begin{array}{*{20}{c}}{\underline {{V_2}} }\\{\underline {{I_2}} }\end{array}} \right] = \left[ {\underline M } \right]\left[ {\begin{array}{*{20}{c}}{\underline {{V_1}} }\\{\underline {{I_1}} }\end{array}} \right]$. Que devient cette relation lorsque $A$ tend vers l’infini ? Quelle relation existe-t-il alors entre les grandeurs réelles ${V_1}$ et ${V_2}$ d’une part, ${i_1}$ et ${i_2}$ d’autre part ?

I-6) Soit $\underline {{Z_1}} $ l’impédance d’entrée du montage précédent, c’est-à-dire, comme indiqué à la figure 3a, l’impédance du dipôle entre la masse et la borne (1), lorsque l’on place une charge d’impédance complexe entre la masse et la borne (2). Soit de même$\underline {{Z_2}} $ l’impédance de sortie du montage de la figure 3b. Exprimer $\underline {{Z_1}} $ et $\underline {{Z_2}} $ en fonction de ${R_1},{R_2}$ et $Z$.

fig. 3a : Montage pour $\underline {{Z_1}} $ d’un quadripôle fig. 3b: Montage pour $\underline {{Z_2}} $ d’un quadripôle
I-7) On pose $K = \frac{{{R_1}}}{{{R_2}}}$. Donner l’expression des impédances $\underline {{Z_1}} $ et $\underline {{Z_2}} $ en fonction de $K$ dans les deux cas suivants : $\underline Z = R$ d’une part, $\underline Z = \frac{1}{{jC\omega }}$ d’autre part, impédance capaci­tive.
Deuxième partie : Réalisation d’un gyrateur
Un gyrateur est un quadripôle travaillant en régime linéaire sinusoïdal dont la matrice admit­tance s’écrit :$\left[ {\begin{array}{*{20}{c}}{\underline {{I_1}} }\\{\underline {{I_2}} }\end{array}} \right] = \left[ {\begin{array}{*{20}{c}}0&{ - \frac{Y}{a}}\\{aY}&0\end{array}} \right]\,\left[ {\begin{array}{*{20}{c}}{\underline {{V_1}} }\\{\underline {{V_2}} }\end{array}} \right]$. Les courants sont comptés positi­ve­ment lors­qu’ils en­trent dans le quadripôle, $Y$ est une admittance réelle positive et $a$ est un réel posi­tif.
II-1) Quel est le rapport entre la puissance moyenne sortante et la puissance moyenne en­trante ?
II-2) En déduire qu’un gyrateur fermé sur un composant qui ne consomme pas de puis­sance simule à l’entrée un composant qui ne consomme pas non plus de puissance.
II-3) Que peut-on dire du quadripôle si $a$ est strictement plus grand que l’unité ?
II-4) Exprimer$\underline {{Z_1}} $ , impédance d’entrée du gyrateur, en fonction de$\underline {{Z_u}} $ impédance placée en sortie. Préciser ces expressions lorsque le quadripôle est fermé sur une inductance $L$, ou sur une capa­cité $C$. C’est plutôt sous cette dernière forme que le gyrateur est généralement uti­lisé. Quelle en est, selon vous, la raison ?

II-5) On considère que dans le schéma de la figure 4, l’amplificateur fonctionne en régime li­néaire. Déterminer la relation entre ${R_1},\;{R_2},\;{R_3}$ et ${R_4}$ pour que la matrice admittance du quadri­pôle ainsi formé soit : $\left[ {\begin{array}{*{20}{c}}{\frac{1}{{{R_1}}}}&{ - \frac{1}{{{R_1}}}}\\{\frac{1}{{{R_4}}}}&0\end{array}} \right]$.

fig. 4 : Schéma de la question II-5) fig. 5 : Une réalisation de gyrateur (question II-9))
II-6) Représenter par ses éléments un quadripôle dont la matrice admittance est : $\left[ {\begin{array}{*{20}{c}}{\frac{1}{{{R_1}}}}&0\\0&0\end{array}} \right]$.
II-7) Représenter par ses éléments un quadripôle dont la matrice admittance est : $\left[ {\begin{array}{*{20}{c}}{ - \frac{1}{{{R_1}}}}&0\\0&0\end{array}} \right]$. On utilisera à cet effet un amplificateur opérationnel, deux résistors de même ré­sistance$R$ et un résistor de résistance ${R_1}$.
II-8) Comment brancher le quadripôle déterminé à la question II-7) sur celui de la fig. 4 pour obtenir un gy­ra­teur ?
II-9) Avec le moins de calculs possibles, montrer que le schéma de la fig. 5 réalise un gyra­teur et, toujours dans le cadre d’un régime de fonctionnement linéaire, don­ner les valeurs de $Y$ et de $a$ qui lui sont associées.
Troisième partie : Utilisation du gyrateur
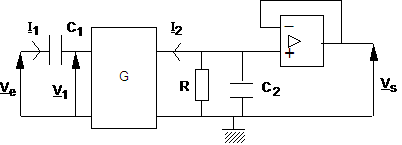
III-1) La fig. 6 représente le gyrateur G de la fig. 5 fermé sur l’association de $R$ et ${C_2}$ mon­tés en parallèle . Déterminer l’expression de la transmittance $\frac{\underline{{{V}_{s}}}}{\underline{{{V}_{e}}}}$du filtre ainsi réalisé (on pourra poser $\omega _0^2 = \frac{1}{{R_1^2{C_1}{C_2}}}$ et $Q = R{C_2}{\omega _0}$). Qu’a-t-on ainsi simulé ?

fig. 6 Filtre accordable utilisant un gyrateur
III-2) Quel est le rôle de l’amplificateur opérationnel en fin de montage ?
III-3) Donner l’expression de la fréquence d’accord, de la largeur de bande passante et du facteur de qualité de ce filtre, en fonction de la valeur de ses composants. Montrer que les ré­glages de la bande passante et de la fréquence d’accord sont indépendants l’un de l’autre.
FIN DE CE PROBLÈME

Première partie : Superposition d’écoulements
On considère l’écoulement d’un fluide incompressible parfait défini par le champ de vitesse ${\vec V_1} = \frac{\lambda }{{2\pi {r_1}}}{\vec u_1}$, où $\lambda $ est une constante réelle et ${r_1},\;{\theta _1}$ et $z$ les coordonnées cylindriques d’un point M par rapport au point A1 de coordonnées $\left( { - a,\;0,\;0} \right)$ dans un repère galiléen $\left( {O,\;x,\;y,\;z} \right)$ muni de la base orthonormée $\left( {\vec x,\;\vec y,\;\vec z} \right)$. Le point $H$ (fig. 1) étant la projection du point M sur le plan $\left( {xOy} \right)$, on a : $\vec{A_{1}M}= {r_1}{\vec u_1} + z\vec z$, où ${\vec u_1}$est le vecteur unitaire porté par $vec{A_{1}H}$.
I-1) Montrer que la circulation du vecteur ${\vec V_1}$ entre deux points A et B est indépendante du chemin suivi et déterminer le potentiel $\varphi {'_1}\left( {{r_1}} \right)$ associé à cet écoulement $\left( {{{\vec V}_1} = + {\bf{grad}}\left( {\varphi _1^{'}} \right)} \right)$, sa­chant qu’il est par conven­tion nul pour une certaine valeur ${r_0}$ de ${r_1}$.
I-2) Cet écoulement suit-il la loi de Laplace $\Delta \varphi _1^{'} = 0$?

fig. 1 : Écoulement défini par ${\vec V_1} = \frac{\lambda }{{2\pi {r_1}}}{\vec u_1}$ fig. 2 : Écoulement défini par ${\vec V_1} + {\vec V_2}$(cf. I-3))
I-3) On superpose à l’écoulement précédent le nouvel écoulement défini par le champ de vi­tesse ${\vec V_2} = \frac{{ - \lambda }}{{2\pi {r_2}}}{\vec u_2}$, avec $\vec{A_{2}M}= \vec{A_{2}H}+ \vec{HM}={r_2}{\vec u_2} + z\vec z$ (fig. 2), les coordonnées du point A2 étant $\left( {a,\;0,\;0} \right)$. Quelle est l’expression du potentiel des vitesses ${\varphi _1}\left( {{r_1},\;{r_2}} \right)$ associé à l’écou­lement ré­sultant, l’origine des potentiels étant prise dans le plan $\left( {yOz} \right)$ ?
I-4) On fait tendre $a$ vers 0 et $\lambda $ vers l’infini, de telle sorte que le produit $2\lambda a=M$soit constant. Montrer que le potentiel en coordonnées cylindriques (vecteurs unitaires ${\vec u_r}$ et ${\vec u_\theta }$) s’écrit alors ${{\varphi }_{1}}=\frac{M\cos \theta }{2\pi r}$, où $\theta $ est l’angle entre $Ox$ et $OH$ (voir fig. 2).
I-5) Déterminer l’équation des lignes de courant ; tracer rapidement leur allure.
I-6) On superpose à cet écoulement un écoulement uniforme, de vitesse $\vec u = u\vec x$. Montrer qu’il existe pour l’écoulement résultant une ligne de courant circulaire d’axe $Oz$, dont on préci­sera le rayon $R$ en fonction de $M$ et de $u$. Donner alors, qualitativement, la forme des lignes de courant ; on distinguera les cas $r$<$R$ et $r$>$R$.

I-7) Un cylindre rigide immobile de rayon $R$ est immergé dans le fluide. La vitesse du fluide pour $r$ très grand devant $R$ est uniforme et égale à $\vec u = u\vec x$. Montrer qu’à l’extérieur du cy­lindre le régime d’écou­lement trouvé en I-6) est solution du problème en présence du cylindre. Existe-t-il des points de vitesse nulle ? Quel est le potentiel ${\varphi _t}$ de l’écoulement ? Voyez-vous une analogie, magnétostatique ou électrostatique, à ce problème d’écoulement ?
I-8) On superpose enfin un dernier écoulement, défini par la vitesse ${\vec V_3}$ pour $r$>$R$: ${\vec V_3} = \frac{C}{{2\pi r}}{\vec u_\theta }$, où $C$ est une constante. Montrer que cet écoulement dérive d’un potentiel ${\varphi _3}$, dont on ne demande pas d’établir l’expression. Quelle est la circulation du vecteur ${\vec V_3}$ sur une courbe fermée dans les deux cas où l’origine est à l’intérieur ou à l’extérieur de la courbe ? Voyez-vous une analogie, magnétostatique ou électrostatique, à ce problème d’écoulement ?
Deuxième partie : Voile de Flettner
Un bateau est muni d’un cylindre vertical de rayon $R$ et de hauteur $h$, tournant autour d’un axe vertical à la vitesse angulaire $\vec \omega = \omega \vec z$. Le vent souffle avec une vitesse uniforme constante $\vec u = u\vec x$. L’écoulement de potentiel des vitesses ${\varphi _t}$ de la question I-7) correspond à l’écoule­ment du vent autour du cylindre de rayon $R$, satisfaisant aux conditions aux limites. L’écoulement de potentiel des vitesses ${\varphi _3}$ de la question I-8) correspond à l’effet d’entraîne­ment de l’air (de masse volumique $\rho $) par la rotation du cylindre.
II-1) Donner la relation entre la constante $C$ et $\omega $. On remarquera que, dans ce modèle, la vitesse du vent sur le cylindre est celle du cylindre, autrement dit que la vitesse tangentielle ne s’annule pas sur la paroi du cylindre (ce point relève, en fait, de la viscosité) .
II-2) Calculer, en coordonnées polaires, les composantes de la vitesse résultante pour $r$>$R$.
II-3) Sachant que, loin du bateau, le vent n’est pas perturbé et que la pression est égale à la pression atmosphérique normale ${p_c}$, déterminer, en fonction de l’angle $\theta $, la pression autour du cylindre ($r$=$R$).
II-4) Quelle est, en fonction de $R$, $C$, $\vec u$, $\vec z$ et de la masse volumique de l’air $\rho $, la résul­tante des forces de pression par unité de hauteur sur le cylindre ? On pourra aussi bien expri­mer le résultat en fonction de $R$, $\rho $, $\vec u$ et $\vec \omega $.
II-5) Préciser sur un schéma le sens de rotation du cylindre correspondant à une force pro­pulsive. Quelle est l’allure du vent la plus favorable (vent de près, vent de travers et vent arrière sont précisés sur la figure 3-a).

fig. 3a : Allures du vent fig. 3b : Voile classique et vent (cf. II-7)) fig. 3c : Bordage optimal

II-6) La vitesse du vent est $10$m.s-1 ; la masse volumique de l’air est $1,3$ kg.m-3. Le cylindre a une hauteur de $10$m et un rayon de $30$cm ; $\omega = 30\;{\rm{rad}}{\rm{.}}{{\rm{s}}^{ - {\rm{1}}}}$. Calculer la valeur numérique maximale de la force propulsive.
Troisième partie : Comparaison avec une voile classique
III-1) Une voile plane d’aire $\Sigma $ et de vecteur unitaire normal $\vec \sigma $ reçoit une veine de vent de vi­tesse $\vec u$ sous l’angle $\alpha $ et la réfléchit selon la loi de Descartes (fig. 3-b). Quel est le vecteur force exercé par le vent sur la voile ? On pourra introduire le débit $D = \rho \Sigma u\sin \alpha $.
III-2) Le bateau reçoit le vent par le travers (fig. 3-c), l’axe du bateau est perpendiculaire au vent relatif. Quelle est dans ces conditions, en fonction de $\rho $, $u$, $\Sigma $ et $\alpha $ la composante pro­pulsive de la force précédente ?
III-3) Pour quelle valeur de $\alpha $ cette composante est-elle maximale ? De quel type de vent s’agit-il ? Calculer numéri­quement la force propulsive maximale avec le même vent qu’en II-6) ($u = 10\,{\rm{m}}{\rm{.}}{{\rm{s}}^{ - {\rm{1}}}},\;\rho = 1,3\,{\rm{kg}}{\rm{.}}{{\rm{m}}^{ - {\rm{3}}}}$) pour une voile de $25$m2. Comparer avec le cylindre de Flettner (le maximum de la fonction $\left( {{{\sin }^2}\alpha } \right)\cos \alpha $ vaut $0,385$).
FIN DE CE PROBLÈME

Concours Physique ENS de Cachan et Lyon 1994 (Corrigé)

E.N.S. Cachan et Lyon 1994; physique; durée 4 h.

A.I.1°) $\Delta \varphi = \frac{{2\pi }}{\lambda }\delta $ avec $\delta =H{{M}_{2}}H'=({{\vec{u}}_{i}}-{{\vec{u}}_{t}}).\overset{\xrightarrow{{}}}{\mathop{{{M}_{1}}{{M}_{2}}}}\,$, ${\vec k_i} = \frac{{2\pi }}{\lambda }{\vec u_i}$, ${\vec k_t} = \frac{{2\pi }}{\lambda }{\vec u_t}$
\( \Rightarrow \Delta \varphi = \overrightarrow {{M_1}{M_2}} .\left( {{{\overrightarrow k }_i} - {{\overrightarrow k }_t}} \right)\)
\(\Delta \varphi = \left( {{{\overrightarrow R }_2} - {{\overrightarrow R }_1}} \right)\left( {{{\overrightarrow k }_i} - {{\overrightarrow k }_t}} \right)\)
A.I.2°) $\Delta \varphi = 2\pi n,\;n \in Z$
A.I.3°) $\Delta \varphi = [({l_2} - {l_1})\vec a + ({m_2} - {m_1})\vec b + ({n_2} - {n_1})\vec c].\vec K = 2\pi n\;\forall \;{l_1},{l_2},{m_1},{m_2},{n_1},{n_2}$
si ${l_2} - {l_1} = 1,\;{m_2} - {m_1} = 0,\;{n_2} - {n_1} = 0$ soit $\vec K.\vec a = 2\pi p$
et ${l_2} - {l_1} = 0,\;{m_2} - {m_1} = 1,\;{n_2} - {n_1} = 0$ soit $\vec K.\vec b = 2\pi q$
et ${l_2} - {l_1} = 0,\;{m_2} - {m_1} = 0,\;{n_2} - {n_1} = 1$ soit $\vec K.\vec c = 2\pi r$ avec $(p,q,r) \in {Z^3}$ et $\vec K = {\vec k_i} - {\vec k_t}$
On peut développer $\vec K$ dans la base des vecteurs réciproques: $\vec K = \alpha \vec A + \beta \vec B + \gamma \vec C$ et tenir compte que $\vec a.\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over A} = 2\pi $, $\vec a.\vec B = 0$ et $\vec a.\vec C = 0$ d’où $\vec K.\vec a = 2\pi \alpha = 2\pi p$ et $\alpha = p$ et de même $\beta = q$, $\gamma = r$; on en déduit:
$\vec K = p\vec A + q\vec B + r\vec C$

Les deux vecteurs d’onde ont la même norme $\left\| {{{\vec k}_i}} \right\| = \left\| {{{\vec k}_t}} \right\|$ et ont leurs extrémités sur un cercle dont le rayon est cette norme; en projetant ces deux vecteurs sur $\vec K$, on obtient: $2{\vec k_i}.\frac{{\vec K}}{K} = \frac{K}{2}$ soit $2{\vec k_i}.\vec K = {K^2}$

A.II.1°) Le volume de la cellule élémentaire est $V = \vec a.(\vec b \wedge \vec c)$; or la surface du parallélélogramme construit sur les vecteurs $\vec a$et $\vec b$ est $S = \left\| {\vec a \wedge \vec b} \right\|$ et si d est la distance entre deux plans atomiques successifs perpendiculaires à $\vec C$ alors V=Sd d’où $d = \frac{{2\pi }}{{\left\| {\vec C} \right\|}}$
A.II.2°) La relation démontrée en A.I.3° s’écrit $2{k_i}\sin \alpha = K$; or $\vec K = r\vec C$ implique $K = r\frac{{2\pi }}{d}$; comme ${k_i} = \frac{{2\pi }}{\lambda }$ on en déduit la relation cherchée: $2d\sin \alpha = r\lambda $ $r \in Z$ (on peut toujours noter s à la place de r).
A.II.3°) La distance interatomique est de l’ordre de 0,1 nm; il faut $\sin \alpha \le 1$ ce qui implique $\lambda \le 2d,\;domaine\;des\;rayons\;X$.
A.III.1°) Par réflexion sur la surface du cristal (parallèle aux plans atomiques équidistants de d), seules les radiations vérifiant la relation $2d\sin \alpha = r\lambda $ont une amplitude non nulle ce qui sélectionne ces radiations; si on veut sélectionner une seule radiation, il faut $\lambda > d$ ce qui correspond à une seule valeur possible de r égale à l’unité.

A.III.2°) Pour faire varier la longueur d’onde, il suffit de faire tourner le cristal; si on dispose de deux cristaux identiques à faces parallèles, le faisceau émergent est parallèle au faisceau incident.
A.IV) La normale en M au cristal est MC; par réflexion, l’angle entre MP et MC est égal à l’angle entre MC et MP’; ils valent $\frac{\pi }{2} - \alpha $; l’angle entre MP et MP’ est constant et vaut$\pi - \alpha $; le point M est sur le cercle de centre C et donc pratiquement sur le cercle de centre C’ au deuxième ordre près; de ce fait P étant fixé, P’ est à l’extrémité d’une corde fixe du cercle de centre C’; en fait P’ est symétrique de P par rapport à CC’.
B.I.1°) On fait un calcul approché voire faux en supposant que les coordonnées de M dépendent peu de celles de P (quasiment fixe); çe qui donne un résultat exact pour le champ magnétique mais pas pour le champ électrique! mais le calcul rigoureux est bien trop difficile pour les étudiants; visiblement, le texte imposait de faire ce calcul faux.
$\vec B = \vec \nabla \wedge \vec A$ soit $\vec B = \frac{{{\mu _0}}}{{4\pi }}\frac{{q\vec \nabla \wedge \vec v(t - \frac{r}{c})}}{r}$ = $\frac{{{\mu _0}q}}{{4\pi }}\left( {\frac{1}{r}\vec \nabla \wedge \vec v(t - \frac{r}{c}) + \vec \nabla \frac{1}{r} \wedge \vec v(t - \frac{r}{c})} \right)$; or $\vec \nabla \frac{1}{r} = - \frac{{\vec r}}{{{r^3}}}$
$\left( {\vec \nabla \wedge \vec v(t - \frac{r}{c})} \right).{\vec u_x} = \frac{\partial }{{\partial y}}{v_z}(t - \frac{r}{c}) - \frac{\partial }{{\partial z}}{v_y}(t - \frac{r}{c})$ d’où $\left( {\vec \nabla \wedge \vec v(t - \frac{r}{c})} \right).{\vec u_x} = \frac{\partial }{{\partial r}}{v_z}(t - \frac{r}{c})\frac{{\partial r}}{{\partial y}} - \frac{\partial }{{\partial r}}{v_y}(t - \frac{r}{c})\frac{{\partial r}}{{\partial z}}$; soit x, y, z les coordonnées de M dans un repère cartésien fixe Oxyz et ${x_P},{y_P},{z_P}$ celles de la charge q, au point P; ${r^2} = {(x - {x_P})^2} + {(y - {y_P})^2} + {(z - {z_P})^2}$; par différentiation: $\frac{{\partial r}}{{\partial x}} = \frac{{x - {x_P}}}{r}$; idem en y et z; par ailleurs $\frac{{\partial f(t - \frac{r}{c})}}{{\partial r}} = - \frac{1}{c}\frac{{\partial f(t - \frac{r}{c})}}{{\partial t}}$; d’où $\left( {\vec \nabla \wedge \vec v(t - \frac{r}{c})} \right).{\vec u_x} = - \frac{1}{c}\left( {\frac{\partial }{{\partial t}}{v_z}(t - \frac{r}{c})\frac{{(x - {x_P})}}{r} - \frac{\partial }{{\partial t}}{v_y}(t - \frac{r}{c})\frac{{(y - {y_P})}}{r}} \right)$; idem pour les composantes y et z; on introduit l’accélération retardée: $\vec a(t - \frac{r}{c}) = \frac{{\partial \vec v(t - \frac{r}{c})}}{{\partial t}}$ et on en déduit: $\vec \nabla \wedge \vec v(t - \frac{r}{c}) = - \frac{1}{c}\vec a(t - \frac{r}{c}) \wedge \frac{{\vec r}}{r}$ et $\vec B = \frac{{{\mu _0}q}}{{4\pi }}\left( {\frac{1}{c}\vec a(t - \frac{r}{c}) \wedge \frac{{\vec r}}{{{r^2}}} - \frac{{\vec r}}{{{r^3}}} \wedge \vec v(t - \frac{r}{c})} \right)$.

B.I.2°) Si M est à grande distance, le second terme en $\frac{1}{{{r^2}}}$ est négligeable devant le premier en $\frac{1}{r}$; d’où $\vec B = \frac{{{\mu _0}q}}{{4\pi c}}\vec a(t - \frac{r}{c}) \wedge \frac{{\vec r}}{{{r^2}}}$; en fait l’approximation correspond à $r > > c\frac{{{v_{ret}}}}{{{a_{ret}}}}$; la dépendance en $\frac{1}{r}$ est prévisible car la puissance rayonnée dans toutes les directions est indépendante de la distance et est proportionnelle au carré de l’amplitude; l’amplitude est donc inversement proportionnelle à la distance r.
B.I.3°) L’onde étant quasi-plane: $\vec E = \vec B \wedge \vec c$ d’où $\vec E = \frac{{{\mu _0}q}}{{4\pi c}}\left( {\vec a(t - \frac{r}{c}) \wedge \frac{{\vec r}}{{{r^2}}}} \right) \wedge \vec c$; avec $\vec c = c\frac{{\vec r}}{r}$, on obtient:
$\vec E = \frac{{{\mu _0}q}}{{4\pi {r^3}}}\left( {\vec a(t - \frac{r}{c}) \wedge \vec r} \right) \wedge \vec r$

B.I.4°) Le vecteur de Poynting est $\vec R = \frac{1}{{{\mu _0}}}\vec E \wedge \vec B$; or $\vec E = \vec B \wedge \vec c$ d’où en remplaçant le champ électrique par sa valeur et en développant le double produit vectoriel, on a: $\vec R = \frac{{{B^2}}}{{{\mu _0}}}\vec c = \frac{{{\mu _0}{e^2}}}{{16{\pi ^2}c{r^2}}}a_{ret}^2{\sin ^2}\theta \frac{{\vec r}}{r}$ ; la puissance rayonnée à travers l’élément de surface (normal à PM) $dS = {r^2}d\Omega $ est $dP = \vec R.d\vec S$; on en déduit:
$\frac{{dP}}{{d\Omega }} = \frac{{{\mu _0}{e^2}}}{{16{\pi ^2}c}}a_{ret}^2{\sin ^2}\theta $ d’où la courbe ci-contre:
B.I.5°) $d\Omega = \sin \theta d\theta d\varphi $
$P=\frac{{{\mu }_{0}}{{e}^{2}}a_{ret}^{2}}{16{{\pi }^{2}}c}\iint\limits_{\begin{smallmatrix}
\theta \in \left[ 0,\pi \right] \\
\varphi \in \left[ 0,2\pi \right]
\end{smallmatrix}}{{{\sin }^{3}}\theta d\theta d\varphi }$ ; l’intégrale $\int\limits_0^\pi {{{\sin }^3}\theta d\theta } = \frac{4}{3}$ et ${\varepsilon _0}{\mu _0}{c^2} = 1$; on en déduit
$P = \frac{{{\mu _0}{e^2}a_{ret}^2}}{{6\pi c}}$ soit une forme plus classique: $P = \frac{2}{3}\;\frac{{{e^2}}}{{4\pi {\varepsilon _0}}}\frac{{a_{ret}^2}}{{{c^3}}}$
B.I.6°) $\vec a_{ret}^2 = \frac{d}{{dt}}({\vec v_{ret}}.{\vec a_{ret}}) - {\vec v_{ret}}.\frac{{d{{\vec a}_{ret}}}}{{dt}}$; on considère les valeurs moyennes sur une période;
$\left\langle {\frac{d}{{dt}}({{\vec v}_{ret}}.{{\vec a}_{ret}})} \right\rangle = \frac{1}{T}\int\limits_0^T {\frac{d}{{dt}}({{\vec v}_{ret}}.{{\vec a}_{ret}})\;} dt = \frac{1}{T}\left[ {{{\vec v}_{ret}}.{{\vec a}_{ret}}} \right]_0^T = 0$ du fait de la périodicité, d’où $\left\langle {\vec a_{ret}^2} \right\rangle = - \left\langle {{{\vec v}_{ret}}.\frac{d}{{dt}}{{\vec a}_{ret}}} \right\rangle $; la puissance perdue en moyenne se met sous la forme: ${P_{perdue}} = + \frac{{{\mu _0}{e^2}}}{{16\pi c}}{\vec v_{ret}}.\frac{{d{{\vec a}_{ret}}}}{{dt}}$
soit sous la forme: ${P_{perdue}} = {\vec F_{ret}}.{\vec v_{ret}}$ c’est-à-dire la puissance d’une force de freinage retardée ${\vec F_{ret}} = + \frac{{{\mu _0}{e^2}}}{{16\pi c}}\;\frac{{d{{\vec a}_{ret}}}}{{dt}}$ soit une force de freinage instantanée: $\vec F = + \frac{{{\mu _0}{e^2}}}{{16\pi c}}\;\frac{{d{{\vec a}_P}}}{{dt}}$.
B.II.1°) Force de Lorentz: $\vec f = - e(\vec E + \vec v \wedge \vec B)$; onde quasi-plane: $\vec E = \vec B \wedge \vec c$; $\left\| {\vec v \wedge \vec B} \right\| \approx vB = \frac{v}{c}E < < E$ car la charge n’est pas relativiste d’où $\vec f \approx - e\vec E$.
B.II.2°) Théorème de la quantité de mouvement pour l’électron: $m\frac{{{d^2}\vec r}}{{d{t^2}}} = - m\omega _0^2\vec r - m\Gamma \vec v + \frac{{{\mu _0}{e^2}}}{{16\pi c}}\;\frac{{d{{\vec a}_P}}}{{dt}} - e\vec E$
B.II.3°) L’équation peut se mettre sous la forme: $-\frac{{{\mu }_{0}}{{e}^{2}}}{16\pi cm}+\ddot{\vec{r}}+\Gamma \dot{\vec{r}}+\omega _{0}^{2}\vec{r}=-\frac{e}{m}\overrightarrow{E}$
On a un mouvement sinusoïdal forcé de pulsation ω; de ce fait la dérivation par rapport au temps est la multiplication par -iω; on en déduit $\vec r = \frac{{\frac{{ - e}}{m}\vec E}}{{\omega _0^2 - {\omega ^2} + i\left( {\Gamma + \frac{{{\mu _0}{e^2}}}{{16\pi cm}}{\omega ^2}} \right)\omega }}$ et l’accélération instantanée en multipliant par -${\omega ^2}$ soit \(\overrightarrow a = \frac{{\frac{e}{m}{\omega ^2}{{\overrightarrow E }_0}{e^{i\left( {{{\vec k}_i}.\overrightarrow {OP} - \omega t} \right)}}}}{{\omega _0^2 - {\omega ^2} + i\left( {\Gamma + \frac{{{\mu _0}{e^2}}}{{16\pi cm}}{\omega ^2}} \right)\omega }}\); l’accélération retardée s’en déduit en remplaçant t par $t - \frac{{PM}}{c}$; attention! ne pas confondre OP et r=PM;
${{\vec{a}}_{ret}}=\frac{\frac{e}{m}{{\omega }^{2}}{{{\vec{E}}}_{0}}{{e}^{i({{{\vec{k}}}_{i}}.\overset{\xrightarrow{{}}}{\mathop{OP}}\,-\omega (t-\frac{PM}{c}))}}}{\omega _{0}^{2}-{{\omega }^{2}}-i\left( \Gamma +\frac{{{\mu }_{0}}{{e}^{2}}}{16\pi cm}{{\omega }^{2}} \right)\omega }$ soit en introduisant ${{\vec{k}}_{r}}=\frac{\omega }{c}\frac{{\vec{r}}}{r}$ et $\vec K = {\vec k_i} - {\vec k_r}$
${{\vec{a}}_{ret}}=\frac{\frac{e}{m}{{\omega }^{2}}{{{\vec{E}}}_{0}}{{e}^{i\vec{K}.\overset{\xrightarrow{{}}}{\mathop{OP}}\,}}}{\omega _{0}^{2}-{{\omega }^{2}}+i\left( \Gamma +\frac{{{\mu }_{0}}{{e}^{2}}}{16\pi cm}{{\omega }^{2}} \right)\omega }{{e}^{i({{{\vec{k}}}_{r}}.\vec{r}-\omega t)}}$ et $\vec{B}=-\frac{{{\mu }_{0}}{{e}^{2}}{{\omega }^{2}}}{4\pi {{r}^{2}}cm}\frac{{{{\vec{E}}}_{0}}\wedge \vec{r}\ {{e}^{i\vec{K}.\overset{\xrightarrow{{}}}{\mathop{OP}}\,}}}{\omega _{0}^{2}-{{\omega }^{2}}+i\left( \Gamma +\frac{{{\mu }_{0}}{{e}^{2}}}{16\pi cm}{{\omega }^{2}} \right)\omega }{{e}^{i({{{\vec{k}}}_{r}}.\vec{r}-\omega t)}}$
On a le champ magnétique d’une onde sphérique issue de O (en $\frac{1}{r}{e^{i({k_r}r - \omega t)}}$) d’amplitude proportionnelle à celle de l’onde plane primaire incidente soit ${\vec E_0}$ et de même pulsation que l’onde primaire (diffusion sans changement de fréquence).
B.II.4°) $\vec R = \frac{1}{{{\mu _0}}}\vec E \wedge \vec B = \frac{{(\vec E + {{\vec E}^*}) \wedge (\vec B + {{\vec B}^*})}}{{4{\mu _0}}}$
$\left\langle {\vec R} \right\rangle = \frac{{\left\langle {\vec E \wedge {{\vec B}^*} + {{\vec E}^*} \wedge \vec B} \right\rangle }}{{4{\mu _0}}}$ avec $\vec E = \vec B \wedge \vec c$ donne $\left\langle {\vec R} \right\rangle = \frac{{\left\langle {\vec B.\vec B} \right\rangle \vec c}}{{2{\mu _0}}} = f(\omega )\frac{{{\mu _0}{e^4}}}{{32{\pi ^2}c{m^2}}}\frac{{{{\sin }^2}\theta }}{{{r^2}}}{\left\| {{{\vec E}_0}} \right\|^2}{\vec u_r}$ avec
$f(\omega ) = \frac{{{\omega ^4}}}{{{{(\omega _0^2 - {\omega ^2})}^2} + {{\left( {\Gamma + \frac{{{\mu _0}{e^2}{\omega ^2}}}{{16\pi cm}}} \right)}^2}{\omega ^2}}}$; $d{P_1} = \left\langle {\vec R} \right\rangle .d\vec S = \left\langle R \right\rangle {r^2}d\Omega $soit $d{P_1} = f(\omega )\frac{{{\mu _0}{e^4}}}{{32{\pi ^2}c{m^2}}}{\sin ^2}\theta {\left\| {{{\vec E}_0}} \right\|^2}d\Omega $

B.II.6°) Avec les valeurs du texte: $T = \frac{{{\mu _0}{e^2}{\omega ^2}}}{{16\pi cm}} < < \Gamma $ si $\omega < < {6,5.10^{18}}\;{s^{ - 1}}$; on ne peut négliger le terme T dans le domaine des rayons X. Si ω → 0 $f(\omega ) \approx {\left( {\frac{\omega }{{{\omega _0}}}} \right)^4} \to 0$ et si ω → ∞ $f(\omega ) = {\left( {\frac{{6\pi cm}}{{{\mu _0}{e^2}}}} \right)^2}\frac{1}{{{\omega ^2}}} \to 0$; pour $\omega = {\omega _0}$, T est négligeable, d’où l’existence du maximum au voisinage de ${\omega _0}$ et la courbe.

B.III.1°) $\frac{{d{P_{1e}}}}{{d{P_{1p}}}} \approx {\left( {\frac{{{m_p}}}{{{m_e}}}} \right)^2} = {1830^2} = {3,3.10^6}$
L’électron rayonne plusieurs millions de fois plus que le proton.
B.III.2°) ${\vec B_p} = - \frac{{{\mu _0}{e^2}{\omega ^2}}}{{4\pi rcm}}\frac{{{{\vec E}_0} \wedge \vec u\;{e^{i\vec K.{{\vec r}_P}}}}}{{\omega _0^2 - {\omega ^2} + i\left( {\Gamma + \frac{{{\mu _0}{e^2}}}{{16\pi cm}}{\omega ^2}} \right)\omega }}{e^{i({{\vec k}_r}.\vec r - \omega t)}}$
B.III.3°) $\vec B = \sum\limits_1^Z {{{\vec B}_p}} $ avec $\vec r$et donc $\vec u$quasiment indépendants du proton, du fait que la distance à l’atome est très supérieure aux dimensions de l’atome.
${\vec B_p} = - \frac{{{\mu _0}{e^2}{\omega ^2}}}{{4\pi rcm}}\frac{{{{\vec E}_0} \wedge \vec u\;\sum\limits_1^Z {{e^{i\vec K.{{\vec r}_P}}}} }}{{\omega _0^2 - {\omega ^2} + i\left( {\Gamma + \frac{{{\mu _0}{e^2}}}{{16\pi cm}}{\omega ^2}} \right)\omega }}{e^{i({{\vec k}_r}.\vec r - \omega t)}}$
B.III.4°) On trouve $\frac{{d{P_Z}}}{{d\Omega }} = \frac{{d{P_1}}}{{d\Omega }}\left\langle {{{\left\| {S(\vec K)} \right\|}^2}} \right\rangle $ avec $S(\vec K) = \sum\limits_1^Z {{e^{i\vec K.{{\vec r}_P}}}} $
B.III.5°) Le déplacement forcé de tous les électrons est le même mais les positions de départ ne sont pas forcément les mêmes: ${\vec r_p} = \vec r + {\vec r_{op}}$.
${\left\| {S(\vec K)} \right\|^2} = \sum\limits_{p = 1}^Z {\sum\limits_{q = 1}^Z {{e^{i\vec K.({{\vec r}_p} - {{\vec r}_q})}}} } $ avec $\vec K = \frac{{2\pi }}{\lambda }(\vec u - {\vec u_z})$
${\left\| {S(\vec K)} \right\|^2} = \sum\limits_{p = 1}^Z {\sum\limits_{q = 1}^Z {{e^{i\vec K.({{\vec r}_{0p}} - {{\vec r}_{0q}}).(\vec u - {{\vec u}_z})}}} } $
${\vec r_{0P}} - {\vec r_{0Q}}$ est de l’ordre de a;
si $\lambda > > a$ les exponentielles valent 1 et ${\left\| {S(\vec K)} \right\|^2} = {Z^2}$; en fait tous les facteurs de phase sont nuls et les Z ondes sont en phase: il s’agit de diffusion cohérente dans ces conditions;
si $\lambda < < a$, on peut écrire ${\left\| {S(\vec K)} \right\|^2} = Z + 2\sum\limits_{\scriptstyle{p = 1}\atop\scriptstyle{p < q}}^Z {\sum\limits_{q = 1}^Z {\cos \frac{{2\pi }}{\lambda }} } (\vec u - {\vec u_z}).({\vec r_{0P}} - {\vec r_{0Q}})$ et si on admet que les valeurs de ${\vec r_{0P}}$ sont aléatoires et que Z est élévé la double somme est nulle; cette fois ${\left\| {S(\vec K)} \right\|^2} = Z$ sauf si $\vec u = {\vec u_z}$ auquel cas ${\left\| {S(\vec K)} \right\|^2} = {Z^2}$; en général, la diffusion est incohérente sauf dans la direction de z’z.
B.IV.1°) ${\vec B_p} = - \frac{{{\mu _0}{e^2}{\omega ^2}}}{{4\pi rcm}}\frac{{{{\vec E}_0} \wedge \vec u\;\sum\limits_1^N {\sum\limits_1^Z {{e^{i\vec K.{{\vec r}_{nP}}}}} } }}{{\omega _0^2 - {\omega ^2} + i\left( {\Gamma + \frac{{{\mu _0}{e^2}}}{{16\pi cm}}{\omega ^2}} \right)\omega }}{e^{i({{\vec k}_r}.(\vec r - {{\vec R}_n}) - \omega t)}}{e^{i{{\vec k}_i}.{{\vec R}_n}}}$; le dernier facteur exponentiel tient compte de la différence de placement des atomes quand ils reçoivent l’onde incidente; par ailleurs $\vec r - {\vec R_n}$ représente le vecteur allant de l’atome considéré au point M considéré.
On en déduit: $\frac{{d{P_N}}}{{d\Omega }} = \frac{{d{P_1}}}{{d\Omega }}\left\langle {{{\left\| {\sum\limits_{n = 1}^N {\left( {\sum\limits_{p = 1}^Z {{e^{i\vec K.{{\vec r}_{nP}}}}} } \right){e^{i\vec K.{{\vec R}_n}}}} } \right\|}^2}} \right\rangle $
B.IV.2°) $\lambda > > \left\| {{{\vec r}_{nP}}} \right\|$ et $\vec K = \frac{{2\pi }}{\lambda }(\vec u - {\vec u_z})$ d’où $\sum\limits_{p = 1}^Z {{e^{i\vec K.{{\vec r}_{nP}}}}} \cong Z$ et $S = Z{S_N}(\vec K)$ avec ${S_N}(\vec K) = \sum\limits_{n = 1}^N {{e^{i\vec K.{{\vec R}_n}}}} $.
B.IV.3°.a) $l = 20\lambda $ et $\vec K \ne \vec 0$; $\left\langle {{{\left\| {{S_N}(\vec K)} \right\|}^2}} \right\rangle = \sum\limits_{n = 1}^N {\sum\limits_{q = 1}^N {{e^{i\vec K.({{\vec R}_n} - {{\vec R}_q})}}} } = N + 2\sum\limits_{\scriptstyle{n = 1}\atop\scriptstyle{n < q}}^N {\sum\limits_{q = 1}^N {\cos (\vec K.({{\vec R}_n} - {{\vec R}_q}))} } $; la double somme est nulle car les vecteurs ${\vec R_n}$ sont aléatoires; d’où $\left\langle {{{\left\| {{S_N}(\vec K)} \right\|}^2}} \right\rangle = N$; on en déduit:
$\frac{{d{P_N}}}{{d\Omega }} = N{Z^2}\frac{{d{P_1}}}{{d\Omega }}$.

B.IV.3°.b) On a la même dépendance que pour un seul électron; mais dans le visible on peut supposer $\omega \cong {\omega _0}$ et $f(\omega ) \cong \frac{{{\omega ^4}}}{{{{(\omega _0^2 - {\omega ^2})}^2}}}$
B.IV.3°.c) On a le phénomène de résonance optique.
B.IV.4°.a) ${S_N}(\vec K) = \sum\limits_{l = 0}^{N - 1} {\sum\limits_{m = 0}^{N - 1} {\sum\limits_{n = 0}^{N - 1} {{e^{i\vec K.(l\vec a + m\vec b + n\vec c)}}} } } $
${S_N}(\vec K) = \sum\limits_{l = 0}^{N - 1} {{e^{i\vec K.l\vec a}}} \sum\limits_{m = 0}^{N - 1} {{e^{i\vec K.l\vec b}}} \sum\limits_{n = 0}^{N - 1} {{e^{i\vec K.l\vec c}}} $
${S_N}(\vec K) = \frac{{{e^{i\vec K.N\vec a}} - 1}}{{{e^{i\vec K.\vec a}} - 1}}\;\frac{{{e^{i\vec K.N\vec b}} - 1}}{{{e^{i\vec K.\vec b}} - 1}}\;\frac{{{e^{i\vec K.N\vec c}} - 1}}{{{e^{i\vec K.\vec c}} - 1}}$
${S_N}(\vec K) = {e^{i\frac{{(N - 1)}}{2}\vec K.(\vec a + \vec b + \vec c)}}\frac{{\sin (\vec K.\frac{N}{2}\vec a)}}{{\sin (\vec K.\frac{{\vec a}}{2})}}\frac{{\sin (\vec K.\frac{N}{2}\vec b)}}{{\sin (\vec K.\frac{{\vec b}}{2})}}\frac{{\sin (\vec K.\frac{N}{2}\vec c)}}{{\sin (\vec K.\frac{{\vec c}}{2})}}$
B.IV.4°.b) $\frac{{d{P_N}}}{{d\Omega }} = {Z^2}{\left( {\frac{{\sin (\vec K.\frac{N}{2}\vec a)}}{{\sin (\vec K.\frac{{\vec a}}{2})}}\frac{{\sin (\vec K.\frac{N}{2}\vec b)}}{{\sin (\vec K.\frac{{\vec b}}{2})}}\frac{{\sin (\vec K.\frac{N}{2}\vec c)}}{{\sin (\vec K.\frac{{\vec c}}{2})}}} \right)^2}\frac{{d{P_1}}}{{d\Omega }}$
Cette fonction est maximale si $\vec K.\vec a = 2\pi p,\;\vec K.\vec b = 2\pi q,\;\vec K.\vec c = 2\pi r$ ce qui est bien le résultat obtenu en A.

B.IV.4°.c)

B.IV.4°.d) $\frac{{d{P_N}}}{{d\Omega }} = {Z^2}{N^4}{\left( {\frac{{\sin (\vec K.\frac{N}{2}\vec c)}}{{\sin (\vec K.\frac{{\vec c}}{2})}}} \right)^2}\frac{{d{P_1}}}{{d\Omega }}$; la largeur angulaire est déterminée par les deux premières annulations de part et d’autre d’un pic principal soit par $\vec K.\frac{N}{2}\vec c = \frac{N}{2}\pi r \pm \pi $ ou $d{\vec k_r}.\vec c = \pm \frac{{2\pi }}{N}$
soit $\Delta {\vec k_r}.\vec c = \frac{{4\pi }}{N}$; or $\left\| {{{\vec k}_r}} \right\| = \frac{{2\pi }}{\lambda }$ et en plus, c’est un vecteur perpendiculaire à ${\vec k_r}$; on en déduit:
$\Delta \theta = \frac{{2\lambda }}{{Nd\cos \theta }}$.
B.IV.5°.a) Au troisième ordre près, ${S_N}(\vec K) \cong \sum\limits_{n = 1}^N {{e^{\vec iK.{{\vec R}_{n0}}}}} (1 + i\vec K.{\vec \rho _n}(t) - \frac{1}{2}{(\vec K.{\vec \rho _n}(t))^2})$
$\left\langle {{{\left\| {{S_N}(\vec K)} \right\|}^2}} \right\rangle = \sum\limits_{n = 1}^N {\sum\limits_{n = q}^N {{e^{i\vec K.({{\vec R}_{n0}} - {{\vec R}_{q0}})}}} \left\langle {(1 + i\vec K.{{\vec \rho }_n}(t) - \frac{1}{2}{{(\vec K.{{\vec \rho }_n}(t))}^2})(1 + i\vec K.{{\vec \rho }_q}(t) - \frac{1}{2}{{(\vec K.{{\vec \rho }_q}(t))}^2})} \right\rangle } $
$\left\langle {{{\left\| {{S_N}(\vec K)} \right\|}^2}} \right\rangle = \sum\limits_{n = 1}^N {\sum\limits_{n = q}^N {{e^{i\vec K.({{\vec R}_{n0}} - {{\vec R}_{q0}})}}} \left\langle {(1 + i\vec K.({{\vec \rho }_n}(t) - {{\vec \rho }_q}(t)) - \frac{1}{2}{{(\vec K.{{\vec \rho }_n}(t))}^2}) - \frac{1}{2}{{(\vec K.{{\vec \rho }_q}(t))}^2} + (\vec K.{{\vec \rho }_n}(t))(\vec K.{{\vec \rho }_q}(t))} \right\rangle } $
or $\left\langle {\vec K.({{\vec \rho }_n}(t) - {{\vec \rho }_q}(t))} \right\rangle = 0$; il reste $\left\langle {{{\left\| {{S_N}(\vec K)} \right\|}^2}} \right\rangle = \sum\limits_{n = 1}^N {\sum\limits_{n = q}^N {{e^{i\vec K.({{\vec R}_{n0}} - {{\vec R}_{q0}})}}} \left\langle {(1 - \frac{1}{2}{{(\vec K.{{\vec \rho }_n}(t))}^2} - \frac{1}{2}{{(\vec K.{{\vec \rho }_q}(t))}^2} + (\vec K.{{\vec \rho }_n}(t))(\vec K.{{\vec \rho }_q}(t))} \right\rangle } $
$\left\langle {{{\left\| {{S_N}(\vec K)} \right\|}^2}} \right\rangle = \sum\limits_{n = 1}^N {\sum\limits_{n = q}^N {{e^{i\vec K.({{\vec R}_{n0}} - {{\vec R}_{q0}})}}} \left\langle {(1 - \frac{1}{2}(\vec K.{{({{\vec \rho }_n}(t) - {{\vec \rho }_q}(t))}^2})} \right\rangle } $
Soit z’z la direction de $\vec K$; $\left\langle {{{\left\| {{S_N}(\vec K)} \right\|}^2}} \right\rangle = \sum\limits_{n = 1}^N {\sum\limits_{n = q}^N {{e^{i\vec K.({{\vec R}_{n0}} - {{\vec R}_{q0}})}}} \left\langle {(1 - \frac{1}{2}({K^2}{{({\rho _{nz}}(t) - {\rho _{qz}}(t))}^2})} \right\rangle } $; en développant le carré parfait, on fait apparaître le double produit de deux déplacements, sans corrélations entre eux; en moyenne, il est nul; on fait apparaître deux carrés de deplacement selon z’z; chaque terme quadratique indépendant représente un degré de liberté et est affecté d’une énergie moyenne kT/2 (k constante de Boltzmann); en appelant C la constante de rappel des atomes à leur position d’équilibre, l’énergie potentielle élastique liée à ce degré de liberté est donnée par $\frac{1}{2}C\left\langle {{\rho ^2}} \right\rangle = \frac{3}{2}kT$ et donc $\left\langle {\rho _{nz}^2} \right\rangle = \frac{{kT}}{C}$

$\left\langle {{{\left\| {{S_N}(\vec K)} \right\|}^2}} \right\rangle = \sum\limits_{n = 1}^N {\sum\limits_{n = q}^N {{e^{i\vec K.({{\vec R}_{n0}} - {{\vec R}_{q0}})}}} (1 - {K^2}} \frac{{kT}}{C})$
On en déduit $\frac{{d{P_N}}}{{d\Omega }} = {Z^2}\frac{{d{P_1}}}{{d\Omega }}\sum\limits_{n = 1}^N {\sum\limits_{n = q}^N {{e^{i\vec K.({{\vec R}_{n0}} - {{\vec R}_{q0}})}}} (1 - {K^2}} \frac{{kT}}{C})$
soit ${\left( {\frac{{d{P_N}}}{{d\Omega }}} \right)_T} = {\left( {\frac{{d{P_N}}}{{d\Omega }}} \right)_{T = 0}}(1 - \varepsilon ) + \xi $ avec $\varepsilon = {K^2}\frac{{kT}}{C}$ et $\xi $représentant le reste du développement.
En conséquence $\varepsilon $est proportionnel à la température absolue.
B.IV.5°.b) ${\left( {\frac{{d{P_N}}}{{d\Omega }}} \right)_T}$ et ${\left( {\frac{{d{P_N}}}{{d\Omega }}} \right)_{T = 0}}$sont proportionnelles et de cefait les maximums et les annulations ont lieu pour les mêmes valeurs de $\theta $; les pics ont donc la même largeur angulaire à T quelconque et au zéro absolu.

Concours Physique ENS de Paris P’ 1994 (Corrigé)

ENS de PARIS P’ 94
ASPECTS D’UN PROCÉDÉ DE MESURE
DE TEMPÉRATURE DE FLAMME
I. Dispositif de mesure.
I.1.a. À l’équilibre thermique, la somme des puissances reçues par le tube est nulle : Wf1 + W21 = 0. On en déduit ${T_f} = {T_1} + \frac{{{h_r}}}{{{h_c}}}\left( {{T_1} - {T_2}} \right)$ .
b. Application numérique : On relève sur la courbe d’étalonnage T1 = 1001,5 °C et T2 = 954 °C, d’où ${T_f} = 1112{\rm{ ^\circ }}C$.
c. Le raisonnement précédent ne tient pas compte des échanges par rayonnement entre la flamme et le tube et des échanges par conduction entre le tube et la paroi du four.
I.2.a. L’application du premier principe de la thermodynamique pendant le temps dt s’écrit : W21 dt = C1 dT1, d’où l’équation $\frac{{d\left( {{T_1} - {T_2}} \right)}}{{dt}} = - \frac{{{h_r}A}}{{{C_1}}}\left( {{T_1} - {T_2}} \right)$, dont la solution est ${T_1} = {T_2} + \left( {{T_1} - {T_2}} \right)\exp \left( { - \frac{{{h_r}{A_t}}}{{{C_1}}}} \right)$.
b. En prenant ΔRs << Rs, on peut utiliser l’expression différentielle : $\Delta t = \frac{{{C_1}}}{{{h_r}A}}\frac{1}{{|{T_2} - {T_1}|}}\frac{{dT}}{{d{R_s}}}\Delta {R_s}$.
c. Application numérique : On tire du graphique $\frac{{dT}}{{d{R_s}}} = 2,6K.{\Omega ^{ - 1}}$, d’où $\Delta t = {8,3.10^{ - 2}}s$.
d. La température du four peut être considérée comme constante pendant la durée de refroidissement précédant l’alarme si son temps caractéristique de variation est petit devant celui du tube, ce qui est le cas si le four est suffisamment thermo-isolé et si sa capacité thermique est grande devant celle du tube.

II. Approche microscopique de la conduction électrique.
II.1.a. On vérifie la condition de normalisation : $\int_0^\infty {p\left( \theta \right)} d\theta = {I_0} = 1$.
b. $\left\langle \theta \right\rangle = \int_0^\infty {\theta p\left( \theta \right)} d\theta = {I_1} = \tau {I_0} = \tau $.
c. $\left\langle {{\theta ^2}} \right\rangle = \int_0^\infty {{\theta ^2}p\left( \theta \right)} d\theta = 2\tau {I_1} = 2{\tau ^2}$.
II.2.a. Les vitesses ${\vec v_k}$ayant une distribution isotrope, leur valeur moyenne est nulle.
b. L’énergie cinétique moyenne d’un électron est $K = \frac{1}{2}m\left\langle {\vec v_k^2} \right\rangle = \frac{1}{2}mv_k^2$, d’où ${v_k} = \sqrt {\frac{{2K}}{m}} $.
c. Application numérique : on obtient ${v_K} = {1,57.10^6}m.{s^{ - 1}}$.
II.3.a. Sous l’action de la force électrique $ - e{\vec E_0}$, un électron prend l’accélération $ - \frac{e}{m}{\vec E_0}$. Sa vitesse devient $\vec v = {\vec v_k} - \frac{e}{m}{E_0}{\vec e_x}t$ et son rayon-vecteur ${\vec r_{k + 1}} = {\vec r_k} - \frac{e}{{2m}}{E_0}{\vec e_x}{\left( {{t_{k + 1}} - {t_k}} \right)^2}$. On en déduit la valeur moyenne $\left\langle {{{\vec r}_{k + 1}} - {{\vec r}_k}} \right\rangle = - N\frac{e}{m}{E_0}{\tau ^2}{\vec e_x}$.
b. La vitesse de dérive s’obtient en prenant la moyenne de $\vec v$ ou en faisant le rapport $\frac{{\left\langle {{{\vec r}_{k + 1}} - {{\vec r}_k}} \right\rangle }}{{N\tau }}:{\vec v_d} = - \frac{{e\tau }}{m}{E_0}{\vec e_x}$.
c. L’équation du mouvement $m\frac{{d\vec v}}{{dt}} = - \zeta \vec v - e{\vec E_0}$conduit au régime permanent $\vec v = - \frac{{e{{\vec E}_0}}}{\zeta }$.
d. $\vec v = {\vec v_d}$en prenant $\zeta = \frac{m}{\tau }$.
II.4.a. De l’expression de la densité de courant $\vec j = - {n_o}e{\vec v_d} = \frac{{{n_o}{e^2}\tau }}{m}{E_0}{\vec e_x}$on tire la conductivité $\sigma = \frac{{{n_o}{e^2}\tau }}{m}$.
b. Application numérique : on obtient $\tau = \frac{{m\sigma }}{{{n_o}{e^2}}} = {4,2.10^{ - 15}}s$.
Les chocs sont très fréquents et le libre parcours moyen $\left( {{v_k}\tau = {{7.10}^{ - 9}}{\rm{ m}}} \right)$est faible.
c. Application numérique : ${v_d} = \frac{\sigma }{{{n_o}e}}{E_0} = 0,73{\rm{ }}m.{s^{ - 1}} < < {v_k}$.
d. Dans un métal $\tau $et $\sigma $diminuent quand la température augmente. Dans un semi-conducteur no et σ augmentent.

II.5.a. L’équation du mouvement de la question 3.c s’écrit en représentation complexe $\left( {1 + i\omega \tau } \right){\vec v_d} = - \frac{{e\tau }}{m}{\vec E_0}$ soit ${\vec v_d} = - \frac{{e\tau }}{m}\frac{{{{\vec E}_0}}}{{1 + i\omega \tau }}$.
b. Comme en 4.a on en déduit la conductivité complexe $\sigma = \frac{{{n_o}{e^2}\tau }}{{m\left( {1 + i\omega \tau } \right)}}$.
c. La conductivité est la même qu’en régime continu pour ωτ << 1 soit pour une fréquence $f < < \frac{1}{{2\pi \tau }} = {3,8.10^{13}}Hz$.
III. Étalonnage.
III.1. On réalise des points fixes au moyen d’équilibres entre phases d’un corps pur. Dans le cas d’un point triple (à trois phases, solide-liquide-vapeur par exemple) le système est monovariant et la température est fixe. Dans le cas d’un équilibre diphasé, la variance est égale à 2 et la température n’est fixée que si l’on fixe la pression (à la valeur de référence de 1 bar par exemple).
III.2. Dans la gamme de quelques centaines d’ohms, le pont de Wheatstone est bien adapté à des mesures de précision.
IV. Étalons de résistance.
IV.1. Résolution.
a. Pour le potentiel considéré, le produit X(x)·Y(y) permet le découplage de l’équation de Schrödinger en deux équations en X(x) et Y(y) : $ - \frac{{{{\rlap{--} h}^2}}}{{2m}}\frac{{{d^2}X}}{{d{x^2}}} = {E_x}X{\rm{ et }} - \frac{{{{\rlap{--} h}^2}}}{{2m}}\frac{{{d^2}Y}}{{d{y^2}}}{E_y}Y$.
b. La solution générale de la première équation est X = A coskx + B sinkx où $k = \frac{{\sqrt {2m{E_x}} }}{{\rlap{--} h}}$.
Les conditions aux limites imposent $\left\{ {B = 0,k = \frac{{\pi + p2\pi }}{{{1_x}}}} \right\}$ou $\left\{ {A = 0,k = \frac{{p2\pi }}{{{1_x}}}} \right\}$, où p est un entier positif, ce qui conduit aux valeurs ${E_x} = {p^2}\frac{{{\pi ^2}{{\rlap{--} h}^2}}}{{2m1_x^2}}$.
c. L’équation en Y(y) conduit à des solutions analogues avec un entier positif q. Les niveaux d’énergie permis ont donc pour valeurs $E = \frac{{{\pi ^2}{{\rlap{--} h}^2}}}{{2m}}\left( {\frac{{{p^2}}}{{1_x^2}} + \frac{{{q^2}}}{{1_y^2}}} \right)$.

IV.2. Conditions aux limites périodiques.
a. kx et ky s’expriment en ${m^{ - 1}}$.
b. La condition de périodicité impose $\exp \left( {i{k_x}{1_x}} \right) = \exp \left( {i{k_y}{1_y}} \right) = 1$, soit ${k_x} = p\frac{{2\pi }}{{{1_x}}}$ et ${k_y} = q\frac{{2\pi }}{{{1_y}}}$, où p et q sont des entiers relatifs non nuls. Les énergies permises s’obtiennent avec l’équation de Schrödinger : $E = \frac{{{{\rlap{--} h}^2}}}{{2m}}\left( {k_x^2 + k_y^2} \right)$.
IV.3. Densité d’états.
a. Les points de coordonnées {kx, ky} se trouvent aux nœuds d’un réseau carré (origine exclue) dont la maille a pour longueurs de base $\Delta {k_x} = \frac{{2\pi }}{{{1_x}}}{\rm{ et }}\Delta {k_y} = \frac{{2\pi }}{{{1_y}}}$.
b. Dans l’espace des $\vec k$, les lignes d’égale énergie sont des cercles centrés sur l’origine, dont l’intérieur correspond aux énergies plus faibles : $k < \frac{{\sqrt {2mE} }}{{\rlap{--} h}}$. Si le nombre de points de ce disque est très grand, ce nombre peut être considéré comme égal au rapport de l’aire du disque à l’aire de la maille : $N\left( E \right)\frac{{\pi {k^2}}}{{ - \Delta {k_x}.\Delta {k_y}}} = \frac{{m{1_x}{1_y}}}{{2\pi {{\rlap{--} h}^2}}}E$.
c. On en déduit $\gamma \left( E \right) = \frac{{m{1_x}{1_y}}}{{2\pi {{\rlap{--} h}^2}}}$.
d. En tenant compte du spin, la densité d’états double : ${\gamma _s}\left( E \right) = \frac{{m{1_x}{1_y}}}{{\pi {{\rlap{--} h}^2}}}$.
IV.4.a. Des expressions obtenues en IV.1.b on déduit les valeurs permises ${k_x} = {p_1}\frac{\pi }{{{1_x}}}$et ${k_y} = {q_1}\frac{\pi }{{{1_{y'}}}}$, avec p et q entiers positifs.
b. La densité d’état s’obtient par les mêmes raisonnements qu’en IV.3.b c et d en les appliquant au quart de disque p>0, q>0, ce qui conduit au même résultat.
IV.5.a. Dans le domaine d’énergie considéré, le nombre d’états est $N = \frac{{m{1_x}{1_y}}}{{\pi {{\rlap{--} h}^2}}}{k_B}T$.
b. Application numérique : on obtient $N = {3,6.10^8}$.
IV.6.a. L’équation du mouvement d’un électron est maintenant $m\frac{{d\vec v}}{{dt}} + \frac{m}{\tau }\vec v = - e\vec E - e\vec v \wedge {\vec B_o}$. On en déduit l’équation en $\vec J$ en régime permanent : ${n_e}{e^2}\vec E = \frac{m}{\tau }\vec J + e\vec J \wedge {\vec B_o}$, qui se met sous la forme matricielle $\left( \begin{array}{l}{E_x}\\{E_y}\end{array} \right) = \frac{1}{{{n_e}e}}\left( {\begin{array}{*{20}{c}}{\frac{m}{{e\tau }}}&{{B_o}}\\{ - {B_o}}&{\frac{m}{{e\tau }}}\end{array}} \right).\left( {\begin{array}{*{20}{c}}{{J_x}}\\{{J_y}}\end{array}} \right)$.
b. L’unité SI de densité de courant de surface est l’ampère par mètre et celle des coefficients de résistivité de surface l’ohm.
c. Avec les nouvelles notations, la matrice s’écrit $\left( {\begin{array}{*{20}{c}}{\frac{1}{{{\sigma _e}}}}&{\frac{\tau }{{{\sigma _e}}}{\omega _c}}\\{ - \frac{\tau }{{{\sigma _e}}}{\omega _e}}&{\frac{1}{{{\sigma _e}}}}\end{array}} \right)$.
ωc est la pulsation cyclotron, vitesse angulaire du mouvement de l’électron dans le champ magnétique.
d. Avec des champs uniformes la tension de Hall est ${V_{Hy}} = - {E_y}{1_y} = \frac{\tau }{{{\sigma _e}}}{\omega _c}\frac{{{1_x}}}{{{1_y}}}{1_y} = \frac{\tau }{{{\sigma _e}}}{\omega _c}{1_x}$, soit ${R_H}\frac{{\tau {\omega _c}}}{{{\sigma _e}}}$qui ne dépend pas des paramètres géométriques.
e. La résistivité longitudinale, coefficient liant Ex et Jx, ne dépend pas de Bo, alors que les trajectoires des électrons entre deux chocs sont courbées par le champ magnétique. L’absence d’un effet magnétorésistif est due à l’hypothèse simplificatrice de régime permanent $\frac{{d\vec v}}{{dt}} = \vec 0$.

IV.7.a. Dans le cas considéré, une température est très basse quand le nombre d’états situés dans l’intervalle kBT est suffisamment petit pour que la quantification ne puisse pas être négligée.
b. Avec les directions imposées ${{B}_{o}}=\frac{{{\underline{A}}_{y}}}{{\underset{\scriptscriptstyle-}{x}}}$, d’où ${A_y} = {B_o}x$.
c. L’équation de la fonction d’onde devient $-\frac{{{{}}^{2}}}{2m}\left( \frac{\underline{{{\Psi }^{2}}}}{{{{\underset{\scriptscriptstyle-}{x}}}^{2}}}+\frac{\underline{{{\Psi }^{2}}}}{{{{\underset{\scriptscriptstyle-}{y}}}^{2}}} \right)+\frac{e}{im}\frac{\underline{\Psi }}{{\underset{\scriptscriptstyle-}{y}}}+\frac{{{e}^{2}}}{2m}B_{o}^{2}{{x}^{2}}\Psi =\varepsilon \Psi $.
d. Les conditions aux limites imposent comme précédemment ${k_y} = q\frac{{2\pi }}{{{1_v}}}$. L’équation prend alors la forme indiquée avec ${V_o}(x) = - \frac{{{{\rlap{--} h}^2}}}{{2m}}k_y^2 + \frac{{\rlap{--} he}}{m}{k_y}{B_o}x + \frac{{{e^2}}}{{2m}}B_o^2{x^2} = \frac{m}{2}{\left( {\frac{{e{B_o}}}{m}} \right)^2}{\left[ {x - \left( { - \frac{{\rlap{--} h{k_y}}}{{e{B_o}}}} \right)} \right]^2}$, d’où ${\omega _o} = \frac{{e{B_o}}}{m}{\omega _c}$et ${x_o} = - \frac{{\rlap{--} h{k_y}}}{{e{B_o}}}$.
e. Vo(x) est un potentiel effectif parabolique pour la fonction Ω(x), équivalent à celui d’un oscillateur harmonique.
IV.8.a. Il faut que $|{k_y}| < \frac{{e{B_o}}}{{\rlap{--} h}}\frac{{{1_x}}}{2}$, ce qui correspond à un nombre de niveaux ${N_y} = 2Ent\left( {\frac{{{1_y}}}{{2\pi }}\frac{{e{B_o}}}{{\rlap{--} h}}\frac{{{1_x}}}{2}} \right) - \frac{{e{B_o}}}{{2\pi \rlap{--} h}}{1_x}{1_y}$. En multipliant ce nombre par 2 pour tenir compte du spin, on obtient bien l’expression de gp.
b. Tous les électrons nelxly se trouve sur le premier niveau (p=0) s’ils sont en nombre inférieur ou égal à g0, soit si ${B_o} = {B_1} = \frac{{\pi \rlap{--} h{n_e}}}{e}$. Les électrons se trouvent au plus sur p niveaux d’énergie si leur nombre est inférieur à $\sum\limits_0^{p - 1} {{g_p} = p{g_0}} $soit pour ${B_o} = {B_p} = \frac{{{B_1}}}{p}$.
c. Pour la valeur Bp, l’expression de la résistance de Hall s’écrit bien $R_H^{(p)} = \frac{{\pi \rlap{--} h}}{{{e^2}}}\frac{1}{p}$, qui ne dépend d’aucune caractéristique du milieu mais des constantes universelles $\rlap{--} h$ et e (effet Hall quantique). Ces résistances s’expriment en ohm.
IV.9.a. On obtient RK = 25,812806·103 Ω (± 12·10‑7 RK).
b. Les deux valeurs de RK concordent à mieux que la précision la plus faible. Il est remarquable que la précision est meilleure pour la valeur expérimentale, ce qui conduit à améliorer notre connaissance de la valeur numérique du rapport $\frac{{\rlap{--} h}}{{{e^2}}}$ de plus d’un ordre de grandeur.
c. La résistance de Hall quantique est reproductible avec une précision meilleure que ce que permettent les définitions du système international d’unités. Il est donc possible et intéressant de l’utiliser comme référence pour la mesure des résistances.
Il faut alors comparer une résistance de Hall à la résistance à mesurer. Comme l’une est longitudinale et l’autre transversale, un montage du type de ceux envisagés à la question III.2 ne convient plus.
IV.10. Quand τ est infini les coefficients ρxx et ρyy sont nuls. La matrice de résistivité est alors $\left( \rho \right) = R_H^{(p)}\left( {\begin{array}{*{20}{c}}0&1\\{ - 1}&0\end{array}} \right)$.
La matrice conductivité est son inverse $\sigma = R_H^{(p) - 1}\left( {\begin{array}{*{20}{c}}0&{ - 1}\\1&0\end{array}} \right)$. On constate que σxx n’est pas l’inverse de ρxx : la résistivité et la conductivité longitudinales sont simultanément nulles.

V. Système de détection.
V.1.a. C’est le montage classique amplificateur non-inverseur : ${V_o} = \frac{{{R_1} + {R_2}}}{{{R_2}}}{I_o}{R_s}$.
b. On en tire ${G_o} = \frac{{{R_1} + {R_2}}}{{{R_2}}}$ .
V.2.a. En égalant ${V_ - } = \frac{{{R_2}}}{{{R_1} + {R_2}}}{V_1}$ et ${V_ + } = {R_s}\frac{{{V_1} + {R_3}{I_o}}}{{{R_s} + {R_3}}}$ on obtient l’équation d’où on tire ${G_1} = {R_3}\frac{{{R_1} + {R_2}}}{{{R_2}{R_3} - {R_1}{R_s}}} = {G_o}\frac{{{R_3}}}{{{R_3} + \left( {1 - {G_o}} \right){R_s}}}$.
b. Quand R3 tend vers l’infini, G1 tend vers Go, comme il était prévisible.
V.3.a. En remplaçant Rs par son expression, on obtient ${V_1} = {V_3}\frac{{1 + aT + b{T^2}}}{{{r_3} + \alpha \left( {1 + aT + b{T^2}} \right)}}$.
On peut développer la fraction rationnelle selon les puissances croissantes de T.
b. En utilisant le paramètre $c = \frac{\alpha }{{{r_3} + \alpha }}$, l’expression s’écrit ${V_1} = \frac{{{V_3}}}{{{r_3} + \alpha }}\frac{{1 + aT + b{T^2}}}{{1 + caT + cb{T^2}}}$. Comme c << 1 (puisque R3 >> Rs) des approximations conduisent à ${V_1} = \frac{{{V_3}}}{{{r_3} + \alpha }}\left[ {1 + aT + \left( {b - c{a^2}} \right){T^2}} \right]$.
c. Pour annuler le terme du second degré, il faut prendre b=ca2, soit ${r_3} = \alpha \left( {\frac{{{a^2}}}{b} - 1} \right)$.
d. α ne devant pas être nul pour réaliser la condition précédente, la plus petite valeur entière possible pour Go est 2. On a alors α = ‑ 1 et ${R_3} = {2,86.10^3}\Omega $ qui est assez grand devant Rs.
Le premier terme négligé dans le développement de V1 est d’ordre 3. Les ordres de grandeurs donnés pour le développement de Rs conduisent à penser que le terme ignoré d’ordre 3 n’a pas d’influence sensible. Il suffit alors de pousser à l’ordre 3 le développement du 3.b. On obtient le coefficient ac(a2c‑2b)=‑8·10‑11. En prenant T=300K, la valeur relative du premier terme négligé est de l’ordre de ${2.10^{ - 3}}$.
V.4.a. En connectant la sonde par deux fils seulement, on mesure la somme de Rs et des résistances des fils de liaisons, mal déterminées (par suite de la non-uniformité de la température par exemple). Le nouvel amplificateur opérationnel permet le passage du courant dans la sonde tout en maintenant la borne C au potentiel de la masse, quelle que soit la résistance du fil parcouru par le courant.
b. Les résultats précédents restent valables puisque les chutes de tension dans les fils d’alimentation de la sonde y ont été supposées nulles. Il faut cependant remarquer que le montage ne permet pas de s’affranchir totalement de l’influence de la résistance R’ du fil reliant la source de courant à la sonde, qui intervient sur la fraction de Io qui traverse la sonde. En en tenant compte, on obtient ${V_1} = \frac{{{R_s}{V_3}}}{{{R_3} + R' + \left( {1 - {G_o}} \right){R_s}}}$. La résistance R’ n’y apparaît qu’au dénominateur alors que, dans le montage à deux fils, elle intervient en se rajoutant à Rs et figure ainsi au numérateur. Devant R3 grande, son influence est bien plus faible dans le montage à quatre fils même si elle n’est pas négligeable devant Rs.
c. Les fils reliant la sonde aux entrées des amplificateurs opérationnels ne sont parcourus que par les courants de polarisation très faibles de ceux-ci et ne servent qu’à la mesure de la tension. Les deux autres servent à l’alimentation en courant de la sonde.
Cette méthode de mesure, dite à quatre fils, permet de mesurer pratiquement la résistance de la sonde même si les longueurs des fils utilisés sont grandes et leur résistances non-négligeable.
VI. Puissance rayonnée par un « corps noir ».

VI.1.a. Les photons frappant la surface δΣ pendant le temps δt sous l’angle d’incidence η se trouvent dans le volume δΣ·cδt·cosη. Parmi les nϕ·δΣ·cδt·cosη photons occupant ce volume, ceux qui arrivent sous un angle d’incidence compris entre η et η+dη en constituent, par suite de l’isotropie à l’équilibre, la proportion égale à la fraction d’angle solide correspondant : ${d^3}N = n\varphi .\delta \Sigma .c\delta .\cos \eta \frac{{2\pi \sin \eta d\eta }}{{4\pi }}$, soit ${d^3}N = \frac{1}{2}{n_\varphi }c\sin \eta \cos \eta \delta \Sigma d\eta \delta t$.
b. La quantité de mouvement du photon a varié de $\Delta p = 2\frac{{hv}}{c}\cos \eta $ selon la normale interne à la paroi, qui a donc reçu la quantité de mouvement opposée.
c. Le théorème de la quantité de mouvement permet de calculer la force exercée sur l’élément de paroi selon la normale externe : ${d^3}F = \frac{{\Delta p}}{{\delta t}}{d^3}NP(E)dE = {n_\varphi }hv\sin \eta {\cos ^2}\eta \delta \Sigma d\eta P(E)dE$. En intégrant sur l’ensemble des énergies des photons on obtient, ${d^2}F = {n_\varphi }\sin \eta {\cos ^2}\eta \delta \Sigma d\eta \int_0^\infty {EP(E)dE} $.
d. En intégrant sur le demi-espace, $\int_0^{\pi /2} {\sin \eta {{\cos }^2}\eta d\eta = \frac{1}{3}} $et $u = {n_\varphi }\int_0^\infty {EP(E)dE} $, d’où $P = \frac{1}{3}u$.
VI.2.a. L’énergie interne est U = uV = 3PV. La différentielle de U est dU = ‑P dV + TdS, d’où on tire $dS = \frac{{dU}}{T} + \frac{P}{T}dV = \frac{V}{T}du + \frac{{4u}}{{3T}}dV$.
b. Sachant que u ne dépend que de T, le théorème de Schwarz appliqué à la fonction S(u,V) donne $\frac{1}{T} = \frac{4}{3}\left( {\frac{1}{T} - \frac{u}{{{T^2}}}\frac{{dT}}{{du}}} \right)$, soit $\frac{{du}}{u} = 4\frac{{dT}}{T}$ qui s’intègre en $u = \zeta .{T^4}$.
c. La différentielle de S(u,V) devient $dS = 4\zeta {T^2}VdT + \frac{4}{3}\zeta {T^3}dV$qui s’intègre en $S = \frac{4}{3}\zeta {T^3}V$.
On en déduit G = U + PV ‑ TS = 0. L’enthalpie libre du gaz de photons est donc toujours nulle. Ce résultat veut dire qu’à T et donc P donnés, G est toujours minimale, et que l’équilibre est toujours possible quel que soit le volume. Cette propriété est due au fait que le nombre de photons est indéterminé par suite de l’existence de l’émission-absorption avec la paroi pour la réalisation de l’équilibre.
VI.3.a. On calcule l’énergie volumique par intégration : $u = \int_0^\infty {{u_v}} dv = \frac{{8\pi h}}{{{c^3}}}{\left( {\frac{{{k_B}T}}{h}} \right)^4}\int_0^\infty {\frac{{{x^3}}}{{\exp \left( x \right) - 1}}} dx = \frac{{8{\pi ^5}}}{{15}}\frac{{k_B^4}}{{{c^3}{h^3}}}{T^4}$, d’où $\zeta = \frac{{8{\pi ^5}}}{{15}}\frac{{k_B^4}}{{{c^3}{h^3}}}$.
b. On reprend le calcul du 1.a en remplaçant la densité des photons nϕ par l’énergie volumique u, ce qui donne $\delta {W_s} = \frac{1}{2}uc\sin \eta \cos \eta d\eta $qui s’intègre en ${W_s} = \frac{1}{4}uc = \frac{{\zeta c}}{4}{T^4}$, et conduit à la valeur annoncée du coefficient σs.
c. On obtient pour la constante de Stefan ${\sigma _s} = {5,66.10^{ - 8}}W.{m^{ - 2}}.{K^{ - 4}}$.
VII. Pyromètre.
VII.1.a. La puissance échangée est égale à la différence entre les puissances reçues et émises dues aux rayonnements en équilibre avec chacune des parois : ${W_{21}} = A{\sigma _s}\left( {T_2^4 - T_1^4} \right)$. Pour une différence de température faible, on peut utiliser le développement limité au premier ordre :
${W_{21}} = 4A{\sigma _s}{T^3}\left( {{T_2} - {T_1}} \right)$.
b. On en déduit la constante $h_r^{th} = 4{\sigma _s}{T^3} = 442W.{m^{ - 2}}.{K^{ - 1}}$, qui est environ trois fois plus grande que la constante hr donnée en I.

c. Si on suppose que le four est un bon corps noir et donc que son facteur d’émissivité est égal à 1, le facteur ε du tube est le seul à intervenir dans les puissances reçues et émises, ce qui entraine $\varepsilon = \frac{{{h_r}}}{{h_r^{th}}}0,32$.
VII.2.a. Le rapport des deux mesures pyrométriques est égal au facteur εν et s’exprime en fonction des températures mesurées T1 et TA selon la loi d’étalonnage de VI.3. à la fréquence ν, en négligeant 1 devant les exponentielles : $\exp \left( {\frac{{hc}}{{{\lambda _o}{k_B}{T_1}}}} \right) = {\varepsilon _v}\exp \left( {\frac{{{h_c}}}{{{\lambda _o}{k_B}{T_A}}}} \right)$.
b. On en tire $\frac{1}{{{T_A}}} = \frac{1}{{{T_1}}} - \frac{{{\lambda _o}{k_B}}}{{hc}}\ln {\varepsilon _v}$.
c. En supposant que le facteur d’émissivité εν est très voisin du facteur d’émissivité moyenne, l’application numérique donne TA = 1195 K soit 922°C. L’écart par rapport à la température réelle est grand : près de 80 K.
____________

Concours Physique ESIGETEL 1993 (Énoncé)

Les Fibres Optiques

ESIGETEL 1993

Les fibres optiques sont des guides de lumière (on dit que la lumière est guidée si elle est contrainte de se propager toujours à l'intérieur de la fibre). Elles sont utilisées notamment en génie des télécommunications pour la transmission de l'information, et en médecine pour les endoscopies. Les lois de l'optique géométrique concernant la propagation de la lumière dans des milieux d'indice variable, expliquent leur Fonctionnement.

On supposera dans l'ensemble de ces exercices que la lumière utilisée est monochromatique.
I. a) Définir l'indice de réfraction d'un milieu transparent, homogène et isotrope.
b) Énoncer les lois de Snell-Descartes de la réflexion et de la réfraction.
c) Tout au long des chemins de propagation de la lumière, définis par les. directions des rayons d'après la loi de la réfraction, quelle est la variable physique optimisée? Donner l'unité de cette variable. Est-elle maximale ou minimale?
d) Décrire les phénomènes de réfraction limite et de réflexion totale.
e) On considère la succession des milieux transparents, homogènes et isotropes E₁, E₂, E₃, E₄ et E₅ d'indices de réfraction n₁, n₂, n₃, n₄, n₅ respectivement. Toutes les interfaces sont planes, parallèles et équidistantes. Un rayon lumineux arrive sur l'interface 1-2 en faisant un angle i₁ avec la normale à cette interface.(Fig. 1).

Écrire la relation liant n_k, n_k+1, i_k et i_k+1 pour les différentes valeurs de k. Trouver un invariant de la propagation. Tracer la marche du rayon.
Dans les questions f), g) et hl), on supposera un rayon incident faisant toujours le même angle i₁ avec la normale à l'interface séparant les deux premiers milieux, comme la Fig.1.
f) Les milieux ont été disposés dans l'ordre des indices de réfraction croissants : ${n_1} < {n_2} < {n_3} < {n_4} < {n_5}$. Y-a-t-il des situations où la lumière ne traverse pas le milieu 5? Justifier la réponse.
g) Est-ce qu'on modifie le résultat obtenu en f) si on intervertit les milieux 2 et 3? Justifier la réponse.
h) Même question qu'en g) si on intervertit les milieux 1 et 2. (Le rayon incident arrive maintenant à l'interface 2-1 avec la même direction qu'il avait précédemment).
i) Donner une cote minimale du diamètre du guide des fibres optiques utilisées dans les endoscopes. Justifier la réponse.
j) Quelle est le phénomène physique le plus important que l'on observe si le diamètre est plus petit que la valeur minimale trouvée en i)?
k) Quelle est la conséquence de ce phénomène sur les fibres optiques?

II.On considère une fibre optique à «saut d'indice». Elle est constituée d'un cylindre transparent, homogène et isotrope d'indice de réfraction n₁, le «coeur», placé entre r=0 et r=a, entouré par une enveloppe coaxiale transparente, homogène et isotrope, d'indice de réfraction n₂, la «gaine», comprise entre r=a et r=b. L'axe de la fibre optique coïncide avec Oz.(Fig2).

Un plan contenant l'axe de symétrie Oz de la fibre est un plan méridien. On ne s'intéresse qu'aux rayons contenus dans ce plan.
a) Pour que cette fibre puisse être utilisée comme guide de lumière il faut imposer une certain relation entre n₁ et n₂ laquelle?
b) Un rayon méridien R faisant à l'entrée de la fibre un angle θ (Cf. Fig 2), sera contraint de rester dans le «coeur» si θ est inférieur à l'angle d'acceptance de la fibre θ_a. Déterminer θ_a en fonction de n₁, n₂ et n_air.
c) Application numérique : Calculer θ_a lorsque n_air=1, n₂=1.43 et n₁=1.45.
d) La fibre optique est maintenant coudée. Expliquer en utilisant un schéma pourquoi une partie des rayons guidés dans la tranche rectiligne ne le sont plus dans la partie coudée.
e)On suppose dans cette partie que la fibre optique prend une position extrême en tournant sur elle même de 180°(F3)

Trouver la relation entre n₁ et n₂ qui assure la réflexion totale, dans la partie coudée, d'un rayon axial (θ=0°).
f) On considère toujours la même fibre optique mais ici on la supposera rectiligne. Sa longueur est L. Calculer en fonction des paramètres de la fibre optique le retard entre un rayon axial et le rayon subissant le nombre maximal de réflexions totales.
g) Application numérique : L = 10 m, n₁ = 1.45 et n₂ = 1.43.

III.Pour diminuer le retard entre les différents rayons se propageant dans le cœur de la fibre on utilise des fibres optiques à «gradient d'indice». Le milieu, à l'intérieur de la fibre, n'est plus homogène. L'indice de réfraction du coeur diminue continûment lorsque l'on s'éloigne de l'axe de la fibre.
Dans la pratique le coeur est constitué d'une cinquantaine de couches, chacune étant transparente, homogène et isotrope, les couches successives étant séparées par des dioptres plans parallèles.
a) En procédant comme dans le cas Ie) mais en supposant maintenant que le nombre de couches augmente indéfiniment en réduisant leurs distances successives, trouver l'expression de l'invariant le long de la propagation.
b) Montrer que la trajectoire suivie par le rayon non axial R au coeur de la fibre (Fig. 4), est définie par l'équation différentielle : ${\left( {\frac{{dr}}{{dz}}} \right)^2} = k{n^2} - 1$ où k est une constante.

c) Intégrer l'équation différentielle IIIb) en supposant que n ne varie que très légèrement dans la fibre suivant la loi:
${n^2} = n_0^2 - (n_0^2 - n_2^2){\left( {\frac{r}{a}} \right)^2}$ pour 0≤ r ≤ a
${n^2} = n_2^2$ pour a≤ r ≤ b
d) Montrer que le rayon R coupe l'axe Oz à des distances d régulièrement espacées.
Trouver d.
e) On veut éviter que les rayons se propageant dans une fibre à «gradient d'indice» atteignent la gaine car ils ne s'y réfléchissent pas, les indices étant égaux en r=a. Quelle condition doit-on imposer à l'angle β₀ pour que r < a?
f) Dessiner l'allure d'un rayon non axial dans une fibre à «gradient d'indice» et dans celle à «saut d'indice» et expliquer qualitativement pourquoi les temps de transit des différents rayons sont plus écartés entre eux dans cette dernière que dans la première.

Conocurs Physique ESEM (Spéciale C) 1993 (Énoncé)

Université d'Orléans
ÉCOLE SUPÉRIEURE DE L'ÉNERGIE ET DES MATÉRIAUX
CONCOURS 1993
Option: Spéciales C
PHYSIQUE
DURÉE : 2 heures ‑ COEFFICIENT : 2
ELECTROPHORESE
Le correcteur tiendra compte du soin apporté à la présentation des solutions ci des résultats
De nombreuses substances en solution, des protéines par exemple, se chargent électriquement, soit par ionisation directe, soit par adsorption d'ions d'autres substances présentes dans la solution.
La technique consistant à séparer des espèces moléculaires ou macromoléculaires dissoutes dans un liquide électriquement conducteur, en fonction de leurs vitesses de migration dans un champ électrique est appelée électrophorèse.
Une procédure possible consiste à déposer le mélange de substances à séparer dans une zone très étroite d'une colonne de solution électrolytique aux extrémités de laquelle est appliquée une différence de potentiel continue (voir figure).

Les substances à séparer, chargées électriquement, se mettent en mouvement sous l'action du champ électrique avec des vitesses de migration différentes.

Ainsi. au cours d'une expérience d'électrophorèse, la zone étroite initiale se sépare au cours du temps en plusieurs zones contenant chacune des espèces moléculaires pures.
Les éventuels mouvements de convection de l'électrolyte constituent un phénomène parasite qu'il convient d'éliminer. On stabilise donc le liquide du point de vue mécanique en l'incluant dans une structure poreuse telle que du papier par exemple.
De plus, les inévitables phénomènes de diffusion constituent une cause d'élargissement des zones au cours du temps.
Le problème proposé étudie les conditions de la séparation en zones distinctes des différentes espèces moléculaires d'un mélange.

PARTIE I. Modélisation de la colonne poreuse.

I‑1) On réalise une colonne poreuse de section S' = 3.0 cm² et de longueur ’ = 30 cm constituée de fibres de cellulose dont la masse volumique vaut ρ = 1,5.10³ kg.m^-3. La masse de la colonne poreuse est M = 53 g
L'espace libre entre les fibres est ensuite imprégné d'un électrolyte de conductivité γ = 1,51 Ω^-1.m^-1 qui le remplit complètement.
Une différence de potentiel U₁ - U₂ = 120 V est appliquée aux extrémités de la colonne. On constate qu'elle est alors parcourue par un courant d'intensité I = 100 mA.
I‑1‑a) Exprimer la conductivité apparente γ' de la colonne, considérée globalement comme un milieu conducteur homogène.
I‑1‑b) Calculer numériquement γ'.
i‑2) On explique la différence observée entre γ et γ' par un double effet :
‑ la présence des fibres isolantes diminue la section réelle de la colonne d'électrolyte pur, qui n'est en fait que S < S'.
‑ la présence des fibres, dont l'orientation est aléatoire, augmente légèrement, pour les ions de l'électrolyte, la distance à parcourir entre les deux électrodes. Cette distance moyenne est alors > ’’.
I‑2‑a) Exprimer le volume S effectivement occupé par l'électrolyte en fonction de S', '. ρ et M.
I‑2‑b) En déduire S et en fonction de S', ’, ρ, M, γ et γ'
I‑2‑c) Calculer numériquement S et .

PARTIE II. Étude du mouvement d'un ion.

Le milieu conducteur étant ainsi modélisé comme une colonne d'électrolyte de conductivité γ, de longueur et de section S, les ions à séparer sont ajoutés dans une zone centrale très étroite, d'épaisseur Δ considérée comme négligeable. On admettra que la présence des ions à séparer ne modifie pas sensiblement la conductivité de l'électrolyte.

II‑1) La différence de potentiel aux extrémités de la colonne étant maintenue à la valeur U₁ - U₂ = 120 V, exprimer le champ électrique $\vec E = E{\vec u_x}$ qui règne dans l’électrolyte ainsi que la force électrostatique $\vec F = F{\vec u_x}$ qui s'exerce sur un ion de charge q.
II‑2) Sous l'effet de cette force, l'ion se met en mouvement. Il est accompagné d'un cortège de molécules d'eau qui lui sont liées par des forces électrostatiques. La masse totale de l'ensemble en mouvement est m. Le mouvement de cet ensemble est freiné par le milieu environnant qui exerce sur
lui une force de frottement $\vec F = - f\vec v = - fv{\vec u_x}$ où $\vec v$ est la vitesse de l'ion et f un coefficient positif qui dépend de l'encombrement de l'ion et de son cortège de molécules liées.
A la date t₀ = 0. l'ion est supposé immobile en 0, origine du repère cartésien Oxyz dans le référentiel lié à la colonne. A cet instant précis, on applique la différence de potentiel U₁ - U₂ = 120 aux extrémités de la colonne.
II‑2‑a) Ecrire l'équation différentielle à laquelle obéit la vitesse v de l'ion en fonction de m, q, E et f.
II‑2‑b) Déterminer l'expression de la vitesse v en fonction du temps.
II‑2‑c) Exprimer. en fonction m, q. E et f, le temps t₁ au bout duquel une vitesse limite V = constante est atteinte à 5 % près.
II‑2‑d) On appelle mobilité de l'ion le coefficient µ tel que: $\vec v = \mu \vec E$.
En prenant comme ordres de grandeurs : m = 10^-25 kg , µ = 5.10^-8 m² . s^-1 . V^-1 et q = 1,6.10^-19 C,
calculer numériquement l'ordre de grandeur de t₁. Que peut‑on en conclure ?
Quel est l'ordre de grandeur de la vitesse limite V ?
En déduire l'ordre de grandeur de la durée possible d'une expérience.

PARTIE III. Etude de la diffusion.

Dans un premier temps, on étudie la diffusion de la zone initiale en l'absence de champ électrique E
On note n(x,y,z,t) la densité de macromolécules (nombre de macromolécules par unité de volume) au point de coordonnées x, y et z, à la date t.
A t = 0, on place les macromolécules en x = 0 avec la densité n₀.

III-1) Justifier que n ne dépend que de x et de t.
Le modèle utilisé est le suivant : les macromolécules diffusent à travers les molécules du milieu en obéissant à la loi de Fick, avec un coefficient de diffusion D $\vec j = - D\frac{{\partial n\left( {x,t} \right)}}{{\partial x}}{\vec u_x}$ où $\vec j$ est le vecteur densité de flux de macromolécules.
III‑2) Quelles sont les unités de j et D ?
III-3) Traduire la conservation de la matière en prenant un système compris entre les abscisses x et x + dx pour trouver une relation entre $\frac{{\partial n\left( {x,t} \right)}}{{\partial t}}$ et $\frac{{\partial j\left( {x,t} \right)}}{{\partial x}}$.
III‑4) En déduire l'équation de la diffusion, équation différentielle dont n(x,t) est solution.
III‑5) Montrer que la fonction : $n\left( {x,t} \right) = \frac{A}{{\sqrt t }}\exp \left( { - \frac{{B{x^2}}}{t}} \right)$ est solution du problème et calculer B. On admettra que : $A = \frac{{{n_0}}}{{\sqrt {4\pi D} }}$.
III‑6) Tracer l'allure des courbes n(x,t) en fonction de x pour différentes dates.
III-7) On rappelle que pour une fonction de probabilité (loi de GAUSS) : $p\left( x \right) = \frac{1}{{\sigma \sqrt {2\pi } }}\exp \left( { - \frac{{{x^2}}}{{2{\sigma ^2}}}} \right)$, la probabilité pour que Ixl > σ est de 5 %.
On appelle largeur de la zone de macromolécules, la longueur Δ de l'intervalle centré sur x = 0 et contenant 95 % des macromolécules.
Déterminer l'expression de la largeur de la zone à la date t.

PARTIE IV. Etude du phénomène général.

On étudie simultanément les phénomènes de diffusion et de séparation des différentes zones sous l'influence du champ électrique appliqué $\vec E$

On veut séparer deux sortes de macromolécules (1) et (2), de concentrations initiales identiques n₀ en x = 0 (et nulles ailleurs), de coefficients de diffusion D₁ et D₂, se déplaçant aux vitesses V₁ et V₂ sous l'effet du champ électrique.
On prendra les valeurs suivantes : D₁ = D_2i = 1,0.10^-9 u.S.I ; V₁ = 20 cm/h ; V₂ = 25 cm/h.
IV‑1) Par quelques graphiques clairs, représenter n₁(x,t) et n₂(x,t) en fonction de x pour plusieurs dates : t₀ = 0, t ₁ > 0 et t₂ > t₁.
IV‑2) A partir de quelle date peut‑on séparer les macromolécules si on considère que la séparation est convenable lorsque le mélange contient moins de 2,5 % de macromolécules (2) dans la zone des macromolécules (1) ?
Remarque : En réalité, on réalise l'expérience pendant une durée plus grande, comme calculé dans la partie II, et on obtient ainsi des espèces moléculaires beaucoup plus pures.