Concours Physique ENS de Lyon et Cachan (PC) 2001 (Corrigé)

Corrigé de l’épreuve de physique du concours ENS Lyon Cachan PC 2001
(diffusion de la lumière par une suspension de billes)
Ce problème fait la théorie d’une expérience relatée par un article de Gilbert Jarry, Elisa Steimer, Vivien Damaschini, Marc Jurczak et Robin Kaiser (J. Opt. 1997 83-89).
I.A.1 Les relations de passage sont :${\vec E_{2T}} = {\vec E_{1T}}\quad n_2^2{E_{2N}} = n_1^2{E_{1N}}\quad {\vec B_2} = {\vec B_1}$.
I.A.2 Appliquons ces relations sur le plan $z = 0$, en tenant compte que pour une onde plane progressive $\underline {\vec B} = \frac{{\vec k}}{\omega } \wedge \underline {\vec E} $ :
$\left\{ \begin{array}{l}{{\vec E}_i} + {{\vec E}_r} = {{\vec E}_t}\\{{\vec B}_i} + {{\vec B}_r} = {{\vec B}_t}\end{array} \right.$
Comme les ondes électromagnétiques sont transversales et comme les ondes considérées sont polarisées selon Oy, ${k_{i,y}} = {k_{r,y}} = {k_{t,y}} = 0$, donc la première loi de Descartes, qui dit que les rayons incident, réfléchi et réfracté et la normale au dioptre sont dans un même plan, est automatiquement vérifiée. Il reste à vérifier que quel que soit $x$ :
${E_0}\exp [i(\omega t - x{k_{i,x}}) + R{E_0}\exp [i(\omega t - x{k_{r,x}})  = T{E_0}\exp [i(\omega t - x{k_{t,x}})$
$\frac{{{{\vec k}_i} \wedge {{\vec e}_y}{E_0}}}{\omega }\exp [i(\omega t - x{k_{i,x}})] + \frac{{{{\vec k}_r} \wedge {{\vec e}_y}R{E_0}}}{\omega }\exp [i(\omega t - x{k_{r,x}})] = \frac{{{{\vec k}_t} \wedge {{\vec e}_y}T{E_0}}}{\omega }\exp [i(\omega t - x{k_{t,x}})]$
Par conséquent : ${k_{i,x}} = {k_{r,x}} = {k_{t,x}}$. Or, ${k_x} = \frac{{n\omega }}{c}\sin (Oz,\vec k)$. Donc l’égalité de ces composantes sur l’axe des x signifie que les rayons incident et réfléchi font des angles opposés avec l’axe $Oz$ et que ${n_1}\sin i = {n_2}\sin i'$.

I.A.3 La continuité de $\vec E$ donne $1 + R = T$ ; celle de $\vec B$ s’écrit
$\frac{{({{\vec k}_i} + R{{\vec k}_r} - T{{\vec k}_t}) \wedge {{\vec e}_y}{E_0}}}{\omega } = \vec 0$, soit ${\left( {{{\vec k}_i} + R{{\vec k}_r} - T{{\vec k}_t}} \right)_z} = 0\quad {\rm{et}}\quad {\left( {{{\vec k}_i} + R{{\vec k}_r} - T{{\vec k}_t}} \right)_x} = 0$
La première de ces deux relations donne${n_1}\cos i - {n_1}\cos i\,R = {n_2}\cos i'\,T$ et la seconde redonne $1 + R = T$.
En résumé, les conditions de passage imposent :
$\left\{ \begin{array}{ccccc}1 + R & = T\\(1 - R){n_1}\cos i\, & = T{n_2}\cos i'\end{array} \right. \Rightarrow R = \frac{{{n_1}\cos i - {n_2}\cos i'}}{{{n_1}\cos i + {n_2}\cos i'}}$
I.A.4 Si ${n_1}$ et ${n_2}$ sont voisins,
$\begin{array}{l}{n_1}\cos i + {n_2}\cos i' \approx 2n\sin \theta \\{n_1}\cos i - {n_2}\cos i' = {n_1}\cos i - {n_2}\sqrt {1 - \frac{{n_1^2{{\sin }^2}i}}{{n_2^2}}} = n\cos i - \sqrt {{{(n + \delta n)}^2} - {n^2}{{\sin }^2}i} = n\cos i - \sqrt {{n^2}{{\cos }^2}i + 2n\delta n + \delta {n^2}} \\ = n\cos i\left( {1 - \sqrt {1 + \frac{{2n\delta n + \delta {n^2}}}{{{n^2}{{\cos }^2}i}}} } \right) \approx - \frac{{\delta n}}{{\cos i}} = - \frac{{\delta n}}{{\sin \theta }}\\R \approx - \frac{{\delta n}}{{2n{{\sin }^2}\theta }}\end{array}$
I.B.1
$\begin{array}{l}\vec r = \overrightarrow {OM} = \overrightarrow {OO'} + \overrightarrow {O'M} = \vec r' - Vt{{\vec e}_z}\\\vec E = {E_0}\exp [i(\omega t + {k_z}Vt - \vec k \cdot \vec r')]{{\vec e}_y}\end{array}$
qui est de la forme demandée si $\omega ' = \omega + {k_z}V\;,\;\vec k' = \vec k$.

I.B.2 Soit $\omega $ est la pulsation commune à l’onde incidente et à l’onde réfléchie dans le référentiel du dioptre. Le référentiel du laboratoire se meut à la vitesse $V{\vec e_z}$ par rapport au dioptre ; dans ce référentiel, l’onde incidente a pour pulsation ${\omega _i} = \omega - {k_{i,z}}V = \omega - Vk\sin \theta $ et l’onde réfléchie ${\omega _r} = \omega - {k_{r,z}}V = \omega + Vk\sin \theta $, donc $\Delta \omega = 2Vk\sin \theta = \frac{{2n\omega V\sin \theta }}{c}$.

I.C.1 La différence de marche entre l’onde réfléchie en $z = 0$ et celle réfléchie en $z = {z_i}$ est $\delta = {n_c}(HI + IK) = 2{z_i}{n_c}\sin {\theta _c} = 2{n_a}\sin {\theta _a}{z_i}$.Le déphasage est $\phi ({z_i}) = \frac{{2\pi \delta }}{{{\lambda _0}}} = \frac{{4\pi {n_a}\sin {\theta _a}{z_i}}}{{{\lambda _0}}}$.
I.C.2 Si $dR = - \frac{1}{{2{n_c}{{\sin }^2}{\theta _c}}}\frac{{\partial n}}{{\partial z}}dz = \frac{{\pi \Delta n}}{{{n_c}{{\sin }^2}{\theta _c}\Lambda }}\sin \left[ {2\pi \left( {ft + \frac{z}{\Lambda }} \right)} \right]dz$ est le facteur de réflexion de l’amplitude d’une couche d’épaisseur dz, alors, à un déphasage d’ensemble $\psi $ près,
$\underline E = \int {dR\,{E_0}\exp (i(\omega t - \phi (z)} )) = \int\limits_{ - L/2}^{L/2} {\frac{{\pi \Delta n{E_0}\exp (i\omega t)}}{{{n_c}{{\sin }^2}{\theta _c}\Lambda }}\sin \left[ {2\pi \left( {ft + \frac{z}{\Lambda }} \right)} \right]\exp \left( { - i\frac{{4\pi {n_a}\sin {\theta _a}z}}{{{\lambda _0}}}} \right)dz} $
Or
$\begin{array}{l}\int\limits_{ - y}^y {\exp (iaz)\sin (bz + c)} dz = \frac{1}{{2i}}\int\limits_{ - y}^y {\left[ {\exp (i((a + b)z + c)) - \exp (i((a - b)z - c))} \right]} dz\\ = \frac{1}{{2i}}\left\{ {\left[ {\frac{{\exp (i((a + b)z + c))}}{{i(a + b)}}} \right]_{ - y}^y - \left[ {\frac{{\exp (i((a - b)z - c))}}{{i(a - b)}}} \right]_{ - y}^y} \right\}\\ = \frac{{\exp (ic)\sin ((a + b)y)}}{{i(a + b)}} - \frac{{\exp ( - ic)\sin ((a - b)y)}}{{i(a - b)}} = \frac{y}{i}[\exp (ic)sinc((a + b)y) - \exp ( - ic)sinc((a - b)y)]\end{array}$
D’où
$\underline E = \frac{{\pi \Delta nL{E_0}\exp (i\omega t)}}{{2i{n_c}{{\sin }^2}{\theta _c}\Lambda }}\left\{ {\exp (i2\pi ft)sinc\left[ {\pi L\left( {\frac{1}{\Lambda } - \frac{{2{n_a}\sin {\theta _a}}}{{{\lambda _0}}}} \right)} \right] - \exp ( - i2\pi ft)sinc\left[ {\pi L\left( {\frac{1}{\Lambda } + \frac{{2{n_a}\sin {\theta _a}}}{{{\lambda _0}}}} \right)} \right]} \right\}$
$K = \frac{{\pi \Delta nL{E_0}}}{{2{n_c}{{\sin }^2}{\theta _c}\Lambda }}\quad \alpha (t) = 2\pi ft$

I.C.3 La fonction $sinc(x)$ est maximum pour $x = 0$, donc les modules des deux termes entre accolades sont maxima, le premier pour ${\theta _a} = {\theta _B} = \arcsin \frac{{{\lambda _0}}}{{2{n_a}\Lambda }}$, le second pour ${\theta _a} = - {\theta _B}$.

La fonction $sinc(x)$ s’annule pour $x = \pm \pi $, donc les modules des deux termes sont nuls, l’un pour $\sin {\theta _a} = \frac{{{\lambda _0}}}{{2{n_a}}}\left( {\frac{1}{\Lambda } \pm \frac{1}{L}} \right)$, l’autre pour les valeurs opposées. Comme $L > > \Lambda > > {\lambda _0}$ , l’intensité émergente présente deux pics très étroits pour deux valeurs petites et opposées de ${\theta _a}$. Voici le graphe de l’intensité en fonction de ${\theta _a}$ exprimé en degrés :

I.C.4 A l’incidence de Bragg, $\delta ({z_i} + \Lambda ) - \delta ({z_i}) = 2{n_a}\sin {\theta _a}\Lambda = {\lambda _0}$, qui est la condition d’interférence constructive.

I.C.5 D’après l’expression démontrée à la question I.C.2, pour ${\theta _a} = {\theta _B}$, le terme principal de $\underline E $ est proportionnel à $\exp (i(\omega + 2\pi f)t)$, donc est décalé en pulsation de $\Delta \omega = + 2\pi f$ ; pour ${\theta _a} = - {\theta _B}$, le terme principal de $\underline E $ est proportionnel à $\exp (i(\omega - 2\pi f)t)$, donc est décalé en pulsation de $\Delta \omega = - 2\pi f$.

Dans le premier cas, la question B.2 prévoit un décalage $\Delta \omega = \frac{{2{n_c}\sin ({\theta _c})V\omega }}{c} = \frac{{{\lambda _0}}}{{2\Lambda }}\frac{{2V\omega }}{c} = 2\pi \frac{V}{\Lambda } = 2\pi f$. Dans le deuxième cas, elle prévoit le décalage opposé, puisque la vitesse du miroir équivalent est dans la disposition contraire.
II.A.1 Sur le détecteur, ${\vec k_0} \cdot \vec r = {\vec k_1} \cdot \vec r = 0$, donc, en moyennant sur un intervalle de temps grand par rapport à la période de la lumière et petit par rapport à la période acoustique :
$\begin{array}{l}s = \eta {b^2}\frac{1}{{{\mu _0}c}}\left\langle {{{\left[ {{E_0}\cos ((\omega + \Delta \omega )t + {\phi _0}) + {E_1}\cos (\omega t + {\phi _1})} \right]}^2}} \right\rangle \\ = \eta {b^2}\frac{1}{{{\mu _0}c}}\left[ {\frac{{E_0^2 + E_1^2}}{2} + 2{E_0}{E_1}\left\langle {\cos ((\omega + \Delta \omega )t + {\phi _0})\cos (\omega t + {\phi _1})} \right\rangle } \right]\end{array}$
Or $\left\langle {\cos ((\omega + \Delta \omega )t + {\phi _0})\cos (\omega t + {\phi _1})} \right\rangle = \frac{1}{2}[\cos (\Delta \omega t + {\phi _0} - {\phi _1})]$
D’où: $s = \eta {b^2}\left[ {{I_0} + {I_1} + 2\sqrt {{I_0}{I_1}} \cos (\Delta \omega t + {\phi _0} - {\phi _1})} \right]$
II.A.2 Supposons les deux ondes polarisées suivant ${\vec e_y}$ et que dans le plan du détecteur ${\vec k_0} \cdot \vec r = 0$ et ${\vec k_1} \cdot \vec r = kx\alpha $.
$\begin{array}{l}s = \eta b\int\limits_{ - b/2}^{b/2} {\frac{1}{{{\mu _0}c}}\left\langle {{{\left[ {{E_0}\cos ((\omega + \Delta \omega )t + {\phi _0}) + {E_1}\cos (\omega t - k\alpha x + {\phi _1})} \right]}^2}} \right\rangle dx} \\ = \eta b\frac{1}{{{\mu _0}c}}\left[ {b\frac{{E_0^2 + E_1^2}}{2} + \int\limits_{ - b/2}^{b/2} {2{E_0}{E_1}\left\langle {\cos ((\omega + \Delta \omega )t + {\phi _0})\cos (\omega t - k\alpha x + {\phi _1})} \right\rangle dx} } \right]\end{array}$
$\left\langle {\cos ((\omega + \Delta \omega )t + {\phi _0})\cos (\omega t - k\alpha x + {\phi _1})} \right\rangle = \frac{1}{2}\cos (\Delta \omega t - k\alpha x + {\phi _0} - {\phi _1})$
Comme $\int\limits_{ - y}^y {\cos (ax + b)dx} = \frac{1}{a}[\sin (ax + b)]_{ - y}^y = \frac{{\sin (ay + b) - \sin ( - ay + b)}}{a} = \frac{{2\sin ay\cos b}}{a} = 2ysinc(ay)\cos b$
$s = \eta {b^2}\left\{ {{I_0} + {I_1} + 2\sqrt {{I_0}{I_1}} \cos (\Delta \omega t + {\phi _0} - {\phi _1})sinc\left( {\frac{{k\alpha b}}{2}} \right)} \right\}$
Si $\alpha $ n’est pas très petit, l’amplitude du terme de battement est très petite.
II.A.3 Le battement est observable si l’argument de la fonction $\sin c$ est inférieur à $\frac{\pi }{2}$, donc si $\alpha < \frac{{{\lambda _0}}}{{2\pi b}}$, soit $\alpha < {10^{ - 4}}rad$.
II.B.1 $s(t)m(t) = \eta {b^2}\left\{ {{I_0} + {I_1} + 2\sqrt {{I_0}{I_1}} \cos (2\pi ft + {\phi _0} - {\phi _1})} \right\}{m_0}\cos (2\pi ft)$
Comme ${\cos ^2}x = \frac{{1 + \cos 2x}}{2}$, la composante continue de $s(t)$ est $s'(t) = \eta {b^2}\sqrt {{I_0}{I_1}} {m_0}\cos ({\phi _0} - {\phi _1})$ ; ${S_1} = {\eta ^2}{b^4}{I_0}{I_1}m_0^2{\cos ^2}({\phi _0} - {\phi _1})$ est proportionnel à ${I_1}$.

II.B.2 Un déplacement très faible d’un miroir de renvoi modifie de façon importante ${\phi _0} - {\phi _1}$.

II.B.3 Considérons le montage de droite. Les montages diviseurs de tension $r,r$ et $R,C$ montrent que $u = \frac{e}{2} = \frac{{{E_M}}}{2}\cos \omega t$ et $\frac{{\underline u - \underline v }}{R} = \frac{{\underline e }}{{R + \frac{1}{{jC\omega }}}}$, soit, si $RC\omega = 1$, $\underline v = \underline u - \frac{{\underline e }}{{1 - j}} = \underline u - \frac{{2\underline u }}{{1 - j}} = \underline u - (1 + j)\underline u = - j\underline u $
$v = {\mathop{\rm Re}\nolimits} \left\{ { - j\frac{{{E_M}}}{2}{e^{j\omega t}}} \right\} = \frac{{{E_M}}}{2}\sin \omega t$. Les tensions $u,v$ fournissent donc les tensions $m,m'$ recherchées, de même amplitude et déphasées de 90°, la masse étant reliée à A et les tensions prélevées en B et D éventuellement à l’aide de montages suiveurs pour ne pas les perturber. Si la masse est située à une des bornes de $e$, il faut interposer un transformateur d’isolement. Ce montage ne fonctionne que pour une fréquence déterminée, mais on peut supposer la fréquence acoustique fixe sans restreindre son utilisation.
II.B.4 ${S_2} = {\left\langle {s(t)m'(t)} \right\rangle ^2} = {\eta ^2}{b^4}{I_0}{I_1}m_0^2{\sin ^2}({\phi _0} - {\phi _1})$. En formant ${S_1} + {S_2}$ (montage sommateur), on obtient un signal proportionnel à ${I_1}$ et insensible aux variations de déphasage.
II.C.1 La lumière diffractée ou réfractée par les billes a changé de direction et donc d’après II.A donne un signal négligeable dans le détecteur.
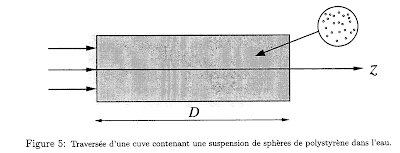
II.C.2 Une tranche de la cuve de section $S$ et d’épaisseur $dz$ contient $\nu S\,dz$ billes qui soumises à l’intensité ${I_c}(z)$ diffusent la puissance ${\sigma _d}\nu S\,dz\,{I_c}(z)$, d’où le bilan énergétique pour la lumière cohérente ${I_c}(z)S = {I_c}(z + dz)S + \nu S\,dz{\sigma _d}\,{I_c}(z)$et l’équation différentielle $\frac{{d{I_c}}}{{dz}} = - \sigma \nu {I_c}$, à variables séparables, qui s’intègre comme $\int\limits_{{I_{c0}}}^{{I_c}(D)} {\frac{{dI}}{I}} = - \sigma \nu D \Rightarrow \ln \frac{{{I_c}(D)}}{{{I_{c0}}}} = - \sigma \nu D \Rightarrow {I_c}(D) = {I_{c0}}\exp ( - \sigma \nu D)$, où ${I_{c0}}$ est l’intensité pénétrant dans la cuve (en pratique c’est plutôt l’intensité que reçoit le détecteur en l’absence de billes, car il faut tenir compte de la réflexion de la lumière par les faces de la cuve, de l’absorption de la lumière par l’eau…).

II.C.3 Soit $V$ le volume d’une bille et $x$ la fraction volumique des billes dans la cuve ; $x = \nu V$ ; le rapport $ - \frac{1}{x}\ln \frac{{{I_c}(D)}}{{{I_{c0}}}}$ prend les valeurs 19800 , 19200 , 19070 et 19400. Le caractère sensiblement constant de ce rapport montre que la loi de Beer-Lambert est vérifiée.

$\begin{array}{l} - \ln \frac{{{I_c}(D)}}{{{I_{c0}}}} = \nu \sigma D = \frac{x}{V}\frac{{24{\pi ^3}{V^2}}}{{\lambda _0^4}}{\left( {\frac{{{{({n_P}/{n_e})}^2} - 1}}{{{{({n_P}/{n_e})}^2} + 2}}} \right)^2}D\\V = \frac{{\lambda _0^4}}{{24{\pi ^3}D}}\frac{1}{x}\left( { - \ln \frac{{{I_c}(D)}}{{{I_{c0}}}}} \right){\left( {\frac{{{{({n_P}/{n_e})}^2} + 2}}{{{{({n_P}/{n_e})}^2} - 1}}} \right)^2} = \frac{{{{(6,328 \cdot {{10}^{ - 7}})}^4}}}{{24{\pi ^3} \times 0,1}} \times 19400 \times {\left( {\frac{{{{(1,59/1,33)}^2} + 2}}{{{{(1,59/1,33)}^2} - 1}}} \right)^2} = 2,67 \cdot {10^{ - 21}}{m^3}\\a = {\left( {\frac{{3V}}{{4\pi }}} \right)^{\frac{1}{3}}} = 8,6 \cdot {10^{ - 8}}m\quad (a < < {\lambda _0})\end{array}$
II.C.4 La précision avancée implique que l’incertitude relative sur $y=-\frac{1}{x}\ln \frac{{{I}_{c}}\left( D \right)}{{{I}_{c0}}}$ soit $\frac{{\Delta y}}{y} = \frac{{\Delta x}}{x} + \left( {\frac{{\Delta {I_c}(D)}}{{{I_c}(D)}} + \frac{{\Delta {I_{c0}}}}{{{I_{c0}}}}} \right)\frac{1}{{\left| {\ln \frac{{{I_c}(D)}}{{{I_{c0}}}}} \right|}} = 0,005 + (0,01 + 0,01)/({\rm{de }}4,95{\rm{ à }}19,4) = {\rm{de }}0,6{\rm{ à }}0,9\;\% $ alors que la dispersion des valeurs de $ - \frac{1}{x}\ln \frac{{{I_c}(D)}}{{{I_{c0}}}}$ est un peu supérieure. D’autre part, il n’est pas facile de mesurer à 1 % près deux intensités dont le rapport est 3.10⁸.
$\frac{{\Delta a}}{a} = \frac{1}{3}\frac{{\Delta V}}{V} = \frac{1}{3}\left( {\frac{{\Delta \ln \frac{{{I_c}(D)}}{{{I_{c0}}}}}}{{\left| {\ln \frac{{{I_c}(D)}}{{{I_{c0}}}}} \right|}} + \frac{{\Delta x}}{x}} \right) = \frac{1}{3}\left( {\frac{{\frac{{\Delta {I_c}(D)}}{{{I_c}(D)}} + \frac{{\Delta {I_{c0}}}}{{{I_{c0}}}}}}{{\left| {\ln \frac{{{I_c}(D)}}{{{I_{c0}}}}} \right|}} + \frac{{\Delta x}}{x}} \right) = \frac{1}{3}\left( {\frac{{0,01 + 0,01}}{{19,4}} + 0,005} \right) = 0,2\;\% $
Pour réaliser cette expérience telle quelle, il faut des billes extrêmement semblables ; l’exploitation de cette méthode permet de déterminer avec précision le rayon des billes ou la répartition de ces rayons.

III.A.1 et III.A.2

La contribution d’un volume $d\tau $ est celle d’un dipôle de moment $\vec Pd\tau $équivalent à la limite de deux charges $ - \rho \,d\tau $ en A et $\rho \,d\tau $ en B telles que $\rho \overrightarrow {AB} = \vec P$. Par conséquent, la sphère polarisée est équivalente à la limite de deux boules de centres O_– et O₊ portant des densités volumiques de charge $ - \rho $ et $ + \rho $ quand $\rho \to \infty \;,\;\rho \overrightarrow {{O_ - }{O_ + }} \to \vec P$.
Lors de ce passage à la limite, cette distribution de charge tend vers une charge répartie sur la surface de la sphère. Un élément $dS$ de cette surface est la limite d’un volume $d\tau = \overrightarrow {dS} \cdot \overrightarrow {{O_ - }{O_ + }} $ qui contient la charge $\rho \,\overrightarrow {dS} \cdot \overrightarrow {{O_ - }{O_ + }} = \vec P \cdot \overrightarrow {dS} $. Donc, la distribution de charge équivalente à la sphère polarisée est la densité superficielle de charge sur la surface de la sphère $\sigma = {P_N} = P\cos \theta $.

III.A.3 A l’extérieur, le potentiel est le même que si l’on avait concentré la charge de la sphère en son centre : ${V_\rho } = \frac{{\rho \frac{4}{3}\pi {a^3}}}{{4\pi {\varepsilon _0}r}}$.

A l’intérieur, le théorème de Gauss permet de calculer le champ électrique : $\begin{array}{l}4\pi {r^2}E = \frac{{\rho \frac{4}{3}\pi {r^3}}}{{{\varepsilon _0}}} \Rightarrow \vec E = \frac{{\rho \vec r}}{{3{\varepsilon _0}}}\quad - \frac{{dV}}{{dr}} = E = \frac{{\rho r}}{{3{\varepsilon _0}}}\quad V = V(a) - \int\limits_a^r {\frac{{\rho r}}{{3{\varepsilon _0}}}\,dr} \\{\rm{si }}r < a\;,\;\,{V_\rho } = \frac{{\rho (3{a^2} - {r^2})}}{{6{\varepsilon _0}}}\quad \quad {\rm{si }}r > a\;,\;\,{V_\rho } = \frac{{\rho {a^3}}}{{3{\varepsilon _0}r}}\end{array}$
III.A.4 En superposant les deux boules de la question II.A.2, on voit que le potentiel est la limite de $\begin{array}{l}{V_{\vec P}}(M) = \frac{{\rho ({O_ - }{M^2} - {O_ + }{M^2})}}{{6{\varepsilon _0}}} = \frac{{\rho (\overrightarrow {{O_ - }M} - \overrightarrow {{O_ + }M} ) \cdot (\overrightarrow {{O_ - }M} + \overrightarrow {{O_ + }M} )}}{{6{\varepsilon _0}}} = \frac{{\rho \overrightarrow {{O_ - }{O_ + }} \cdot (\overrightarrow {{O_ - }M} + \overrightarrow {{O_ + }M} )}}{{6{\varepsilon _0}}}\\{V_{\vec P}}(M) = \frac{{\vec P \cdot \vec r}}{{3{\varepsilon _0}}} \Rightarrow {E_{\vec P}} = - \,\overrightarrow {grad} \,V = - \frac{{\vec P}}{{3{\varepsilon _0}}}\end{array}$
L’expression du champ électrique s’obtient plus directement en superposant les champs électriques des deux boules de III.A.2 : ${\vec E_{\vec P}} = - \frac{{\rho \overrightarrow {{O_ - }M} }}{{3{\varepsilon _\`a }}} + \frac{{\rho \overrightarrow {{O_ + }M} }}{{3{\varepsilon _\`a }}} = - \frac{{\rho \overrightarrow {{O_ - }{O_ + }} }}{{3{\varepsilon _\`a }}} = - \frac{{\vec P}}{{3{\varepsilon _\`a }}}$.

III.B.1 $\overrightarrow {rot} \,\vec E = - \frac{{\partial \vec B}}{{\partial t}}\quad \overrightarrow {rot} \,\vec H = \vec j + \frac{{\partial \vec D}}{{\partial t}}\quad div\,\vec B = 0\quad div\,\vec D = \rho $

III.B.2 A la traversée d’une surface, sont continus ${\vec E_T},{B_N}$ ; ${D_{N2}} - {D_{N1}} = \sigma \quad {\vec H_{T2}} - {\vec H_{T1}} = {\vec j_S} \wedge {\vec n_{12}}$
III.B.3 Le champ incident et le champ total doivent vérifier les équations de Maxwell dans le vide ; comme les équations de Maxwell sont linéaires, elles sont vérifiées par le champ diffusé qui est la différence du champ total et du champ incident.
III.B.4 et III.B.5 On peut remplacer la polarisation électrique par une distribution de charge sur la sphère ${\sigma _{lié }} = {P_N} = P\cos \theta $ et une distribution de courant dans la sphère ${j_{lié }} = \frac{{\partial \vec P}}{{\partial t}}$.
III.B.6 Dans une bille, $\vec D = {\varepsilon _0}\vec E + \vec P = {\varepsilon _P}\vec E \Rightarrow \vec P = ({\varepsilon _P} - {\varepsilon _0})\vec E$.
III.C.1 Les potentiels sont proportionnels aux courants et aux charges tels qu’ils étaient antérieurement, le retard considéré étant la durée de propagation de la lumière de la source à l’effet. Ce retard s’exprime par le terme $\exp ( - ik\left\| {\vec r - \vec r'} \right\|)$.
III.C.2 Si on peut négliger le terme de propagation, $\underline{{\vec{A}}}_{d}^{\operatorname{int}}(\vec{r})=\frac{{{\mu }_{0}}{{\underline{{\vec{j}}}}_{li\acute{e}}}}{4\pi }\iiint_{bille}{\frac{{{d}_{3}}{r}'}{\left\| \vec{r}-{\vec{r}}' \right\|}}$ a la même forme que le potentiel dans une boule uniformément chargé en volume $\underline{V}(\vec{r})=\frac{\rho }{4\pi {{\varepsilon }_{0}}}\iiint_{bille}{\frac{{{d}_{3}}{r}'}{\left\| \vec{r}-{\vec{r}}' \right\|}}=\frac{\rho (3{{a}^{2}}-{{r}^{2}})}{6{{\varepsilon }_{0}}}$. Donc $\underline {\vec A} _d^{{\mathop{\rm int}} }(\vec r) = \frac{{{\mu _0}{{\vec j}_{li\'e }}(3{a^2} - {r^2})}}{6}$.
III.C.3 La condition de jauge de Lorentz est $\frac{{\partial \underline A _d^{{\mathop{\rm int}} }}}{{\partial z}} + \frac{{i\omega {{\underline V }_d}}}{{{c^2}}} = 0$.
$\begin{array}{l}\underline V _d^{{\mathop{\rm int}} } = - \frac{{{c^2}}}{{i\omega }}\frac{{\partial \underline A _d^{{\mathop{\rm int}} }}}{{\partial z}} = \frac{{{\mu _0}{c^2}{{\underline j }_{lié }}z}}{{3i\omega }}\\\underline {\vec E} _d^{{\mathop{\rm int}} } = - i\omega \underline {\vec A} _d^{{\mathop{\rm int}} } - \,\overrightarrow {grad} \,\underline V _d^{{\mathop{\rm int}} } = \frac{{ - i\omega {\mu _0}{{\underline {\vec j} }_{lié }}(3{a^2} - {r^2})}}{6} - \frac{{{\mu _0}{c^2}{{\underline {\vec j} }_{lié }}}}{{3i\omega }} \approx - \frac{{{\mu _0}{c^2}{{\underline {\vec j} }_{lié}}}}{{3i\omega }} = - \frac{{{{\underline {\vec j} }_{lié}}}}{{3{\varepsilon _0}i\omega }}\end{array}$
car $a\omega < < c$ puisque $a < < {\lambda _0}$.
$\underline {\vec B} _d^{{\mathop{\rm int}} } = \,\overrightarrow {rot} \underline {\vec A} _d^{{\mathop{\rm int}} } = \,\frac{{{\mu _0}\,\overrightarrow {grad} \,(3{a^2} - {r^2}) \wedge \underline {\vec j} _d^{{\mathop{\rm int}} }}}{6} = \frac{{{\mu _0}\vec r \wedge \underline {\vec j} _d^{{\mathop{\rm int}} }}}{3}$

III.C.4
$\begin{array}{l}\underline {\vec E} _d^{{\mathop{\rm int}} } \approx - \frac{{{\mu _0}{c^2}{{\underline {\vec j} }_{lié }}}}{{3i\omega }} = - \frac{{\underline {\vec P} }}{{3{\varepsilon _0}}} = - \frac{{({\varepsilon _P} - {\varepsilon _0})({{\underline {\vec E} }_i} + \underline {\vec E} _d^{{\mathop{\rm int}} })}}{{3{\varepsilon _0}}}\\\underline {\vec E} _d^{{\mathop{\rm int}} } = \frac{{{\varepsilon _P} - {\varepsilon _0}}}{{{\varepsilon _P} + 2{\varepsilon _0}}}{\underline {\vec E} _i}\end{array}$
qui est bien uniforme à l’ordre 0 en $\omega $. Les termes d’ordre supérieur ne sont pas uniformes. $\underline {\vec B} _d^{{\mathop{\rm int}} } = \,\frac{{{\mu _0}\vec r \wedge \underline {\vec j} _d^{{\mathop{\rm int}} }}}{3}$ n’est pas uniforme, mais est d’ordre 1 par rapport à $\omega $ et doit donc être négligé : $\underline {\vec B} _d^{{\mathop{\rm int}} } = \vec 0$.
III.D.1 Pour calculer le champ électromagnétique loin de la bille, il faut négliger $r'$ dans l’expression (25), car $r' < < r$ et $r' < < {\lambda _0}$. D’où : ${\underline {\vec A} _d} = {\underline {\vec A} _0}\frac{{\exp ( - ikr)}}{r}\quad {\underline {\vec A} _0} = \frac{{{\mu _0}V{{\underline {\vec j} }_{li\'e }}}}{{4\pi }}\quad V = \frac{4}{3}\pi {a^3}$
Il vaut mieux écrire une expression en fonction du volume $V$ de la sphère que de $a$.

III.D.2

$\begin{array}{l}{\underline V _d} = - \frac{{{c^2}}}{{i\omega }}div\,{\underline {\vec A} _d} = - \frac{{{c^2}}}{{i\omega }}\frac{\partial }{{\partial z}}\left( {{{\underline A }_0}\frac{{\exp ( - ikr)}}{r}} \right)\\{r^2} = {x^2} + {y^2} + {z^2}\quad 2r\,dr = 2z\,dz\quad \frac{{\partial f(r)}}{{\partial z}} = \frac{z}{r}\frac{{df(r)}}{{dr}} = \cos \theta \frac{{df(r)}}{{dr}}\\{\underline V _d} = - \frac{{{c^2}{{\underline A }_0}\cos \theta }}{{i\omega }}\frac{d}{{dr}}\left( {\frac{{\exp ( - ikr)}}{r}} \right)\\{\underline E _{d,r}} = - i\omega {\underline A _0}\cos \theta \frac{{\exp ( - ikr)}}{r} - \frac{{\partial {{\underline V }_d}}}{{\partial r}} = {\underline A _0}\cos \theta \left( { - i\omega \frac{{\exp ( - ikr)}}{r} + \frac{{{c^2}}}{{i\omega }}\frac{{{d^2}}}{{d{r^2}}}\left( {\frac{{\exp ( - ikr)}}{r}} \right)} \right)\\{\underline E _{d,\theta }} = i\omega {\underline A _0}\sin \theta \frac{{\exp ( - ikr)}}{r} - \frac{1}{r}\frac{{\partial {{\underline V }_d}}}{{\partial \theta }} = {\underline A _0}\sin \theta \left( {i\omega \frac{{\exp ( - ikr)}}{r} - \frac{{{c^2}}}{{i\omega }}\frac{1}{r}\frac{d}{{dr}}\left( {\frac{{\exp ( - ikr)}}{r}} \right)} \right)\end{array}$
Quand $r \to \infty $, au premier ordre en $\frac{1}{r}$, $\frac{{{d^2}}}{{d{r^2}}}\left( {\frac{{\exp ( - ikr)}}{r}} \right) \approx - {k^2}\frac{{\exp ( - ikr)}}{r}$. Alors, comme $k = \frac{\omega }{c}$, le terme en $\frac{1}{r}$ de ${\underline E _{d,r}}$est nul. Donc :${\underline {\vec E} _d} \approx i\omega {\underline A _0}\sin \theta \frac{{\exp ( - ikr)}}{r}{\vec e_\theta }$
III.D.3 La structure locale du champ électrique est celle d’une onde plane. En effet, les surfaces d’onde sont des sphères de centre l’origine, soit localement les plans perpendiculaires à la direction radiale ; le champ électrique est perpendiculaire à la propagation et d’amplitude localement constante. L’intensité est $\left\langle {\frac{{{{({{\vec E}_d} \wedge {{\vec B}_d})}_r}}}{{{\mu _0}}}} \right\rangle = \frac{{{\varepsilon _0}c{{\left| {{{\underline E }_d}} \right|}^2}}}{2}$.
III.D.4 ${{P}_{d}}=\iint\limits_{\text{sph }\!\!\grave{\mathrm{e}}\!\!\text{ re}}{\frac{{{\varepsilon }_{0}}c{{\left| {{\underline{E}}_{d}} \right|}^{2}}}{2}dS=\int\limits_{0}^{\pi }{\frac{{{\varepsilon }_{0}}c{{\omega }^{2}}{{\sin }^{2}}\theta {{\left| {{\underline{A}}_{0}} \right|}^{2}}}{2{{r}^{2}}}2\pi {{r}^{2}}\sin \theta \,d\theta }}=\pi {{\varepsilon }_{0}}c{{\omega }^{2}}{{\left| {{\underline{A}}_{0}} \right|}^{2}}\int\limits_{0}^{\pi }{{{\sin }^{3}}\theta \,d\theta }$
Le changement de variable $u = \cos \theta $ permet de calculer $\int\limits_0^\pi {{{\sin }^3}\theta \,d\theta } = 2\int\limits_0^{\pi /2} {{{\sin }^3}\theta \,d\theta } = - 2\int\limits_1^0 {(1 - {u^2})\,du} = \frac{4}{3}$.
${P_d} = \frac{4}{3}\pi {\varepsilon _0}c{\omega ^2}{\left| {{{\underline A }_0}} \right|^2}$.

III.D.5 En III.D1 : ${\underline {\vec A} _0} = \frac{{{\mu _0}V{{\underline {\vec j} }_{lié }}}}{{4\pi }}$ ; en III.C.3 : $\underline {\vec E} _d^{{\mathop{\rm int}} } = \frac{{{{\underline {\vec j} }_{li\'e }}}}{{3{\varepsilon _0}i\omega }}$ ; en III.C.4 : $\underline {\vec E} _d^{{\mathop{\rm int}} } = \frac{{{\varepsilon _P} - {\varepsilon _0}}}{{{\varepsilon _P} + 2{\varepsilon _0}}}{\underline {\vec E} _i}$.
D’où : ${P_d} = \frac{{4\pi {\varepsilon _0}c{\omega ^2}}}{3}{\left( {\frac{{{\mu _0}V}}{{4\pi }}} \right)^2}{(3\omega {\varepsilon _0})^2}{\left( {\frac{{{\varepsilon _P} - {\varepsilon _0}}}{{{\varepsilon _P} + 2{\varepsilon _0}}}} \right)^2}{\left| {{{\underline {\vec E} }_i}} \right|^2} = \frac{{3{\varepsilon _0}{V^2}{\omega ^4}}}{{4\pi {c^3}}}{\left( {\frac{{{\varepsilon _P} - {\varepsilon _0}}}{{{\varepsilon _P} + 2{\varepsilon _0}}}} \right)^2}{\left| {{{\underline {\vec E} }_i}} \right|^2}$.
III.D.6 ${I_i} = \frac{1}{2}{\varepsilon _0}c{\left| {{{\underline {\vec E} }_i}} \right|^2}$
${\sigma _d} = \frac{{{P_d}}}{{{I_i}}} = \frac{{3{V^2}{\omega ^4}}}{{2\pi {c^4}}}{\left( {\frac{{{\varepsilon _P} - {\varepsilon _0}}}{{{\varepsilon _P} + 2{\varepsilon _0}}}} \right)^2} = \frac{{24{\pi ^3}}}{{\lambda _0^4}}{\left( {\frac{{{\varepsilon _P} - {\varepsilon _0}}}{{{\varepsilon _P} + 2{\varepsilon _0}}}} \right)^2}{V^2}$
III.D.7 Cette expression est semblable à celle de II.C.3, en y replaçant $\frac{{{\varepsilon _P}}}{{{\varepsilon _0}}}$ par $\frac{{n_P^2}}{{n_e^2}}$, ce qui se comprend si l’on considère que l’indice $n$ d’un milieu est $\sqrt {{\varepsilon _r}} = \sqrt {\frac{\varepsilon }{{{\varepsilon _0}}}} $ et que seul compte l’indice apparent des billes, c’est-à-dire le rapport de leur indice à celui du milieu où elles baignent.

Concours Physique ENS de Lyon et Cachan (PC) 2001 (Énoncé)

LC 123 J. 5116
SESSION 2001
______
Filière Physique - Chimie
______
PHYSIQUE
(Épreuve commune aux ENS: Lyon et Cachan)
Durée : 5 heures
______
L'usage de calculatrices électroniques de poche à alimentation autonome, non imprimantes et sans document d'accompagnement, est autorisé. Cependant, une seule calculatrice à la fois est admise sur la table ou le poste travail, et aucun échange n'est autorisé entre les candidats.
Un liquide contenant des particules microscopiques en suspension diffuse la lumière incidente dans toutes les directions. Un objet immergé dans un tel liquide n'est donc pas toujours visible à l'oeil nu. Il peut cependant être détecté par l'analyse du rayonnement transmis dans la direction d'incidence. L'intérêt de cette détection, en imagerie biomédicale par exemple, justifie l'étude du rayonnement diffusé. Dans ce problème, on étudie la diffusion de lumière dans un milieu modèle constitué par une suspension dans l'eau de sphères de polystyrène microscopiques.
Dans la première partie, on étudie le principe d'un modulateur acousto-optique, qui permet de décaler la fréquence d'une onde optique en lui faisant traverser un cristal parcouru par une onde acoustique.
La deuxième partie est consacrée à l'étude d'un dispositif expérimental, utilisant entre autres le modulateur étudié dans la première partie, et permettant l'étude quantitative du phénomène.
On s'intéresse dans la troisième partie au calcul du champ électromagnétique diffusé par une unique sphère de polystyrène, ce qui permet de justifier l'expression de la section efficace de diffusion utilisée dans la deuxième partie.
Les trois parties sont largement indépendantes.
Il est demandé aux candidats de rappeler les numéros identifiant une question avant la solution qu'ils proposent.
Tournez la page S.V.P.

• Notations

• Dans tout le problème, l'espace est rapporté à trois axes Ox, Oy, Oz, auxquels est associée la base orthonormée directe ${\vec e_x}$, ${\vec e_y}$, ${\vec e_z}$ . Le point M de l'espace est repéré par le vecteur $\vec r = \overrightarrow {OM} $ .
• On utilise pour les fonctions sinusoïdales du temps la notation complexe. La fonction réelle $x = {X_m}\cos (\omega t + \varphi )$ sera notée, en omettant, pour alléger l'écriture, le symbole Re (partie réelle) :
$x = {X_m}\exp \left[ {i(\omega t + \varphi )} \right]$
L'amplitude complexe X de x est définie par :
$\underset{\scriptscriptstyle-}{X}={{X}_{m}}\exp (i\varphi )$
On rappelle que la valeur moyenne sur une période $T = \frac{2\pi }{ \omega }$ du produit de deux fonctions sinusoïdales ${x_1}(t) = {X_{1m}}\cos (\omega t + {\varphi _1})$ et ${x_2}(t) = {X_{2m}}\cos (\omega t + {\varphi _2})$ s'exprime simplement en fonction de leurs amplitudes complexes :
$\frac{1}{T}\int_{0}^{T}{{{x}_{1}}(t)\ {{x}_{2}}(t)\ dt=}\frac{1}{2}R\text{e}\left[ {{{\underset{\scriptscriptstyle-}{X}}}_{1}}\underset{\scriptscriptstyle-}{X}_{2}^{*} \right]=\frac{1}{2}R\text{e}\left[ \underset{\scriptscriptstyle-}{X}_{1}^{*}{{{\underset{\scriptscriptstyle-}{X}}}_{2}} \right]$
où ${{\underset{\scriptscriptstyle-}{X}}^{*}}$ désigne le complexe conjugué de X.
• La notation sinc désigne le sinus cardinal défini par : ${\rm{sinc}}(x) = \frac{\sin (x)}{x}$.
• c désigne la vitesse de la lumière dans le vide, ${\varepsilon _0}$ la permittivité du vide, et ${\mu _0}$ la perméabilité du vide.

• Formulaire

${\rm{div}}\,(f\,\vec A) = f\,{\rm{div}}\,\vec A + \overrightarrow {{\rm{grad}}} (f)\,.\,\vec A$ (1)
$\overrightarrow {{\rm{rot}}} \,(f\,\vec A) = f\,\overrightarrow {{\rm{rot}}} \,\vec A + \overrightarrow {{\rm{grad}}} (f)\, \wedge \,\vec A$ (2)
I Modulateur acousto-optique

I.A
On considère deux milieux diélectriques, non magnétiques, homogènes et isotropes, d'indices de réfraction n₁ et n₂ . Le milieu d'indice n₁ occupe le demi-espace z < 0 , le milieu d'indice n₂ le demi-espace z > 0. Le plan z = 0 constitue ainsi un dioptre plan.
Une onde plane progressive, monochromatique de pulsation ω , se propage dans le milieu d'indice n₁ . Le champ électrique ${\vec E_i}$ de cette onde est polarisé rectilignement selon ${\vec e_y}$ ; son vecteur d'onde ${\vec k_i}$ fait avec Oz un angle i (angle d'incidence). On admet que les ondes réfléchies et transmises par le dioptre sont planes, monochromatiques de pulsation ω , de champs électriques ${\vec E_r}$ et ${\vec E_t}$ polarisés selon ${\vec e_y}$.
Les champs électriques, à l'instant t et au point M de l'espace, sont écrits sous la forme
${\vec E_i}(\vec r,t) = {E_0}\,\exp \left[ {i(\omega t - {{\vec k}_i}\,.\,\vec r)} \right]{\vec e_y}$ (3)
${\vec E_r}(\vec r,t) = R\,{E_0}\,\exp \left[ {i(\omega t - {{\vec k}_r}\,.\,\vec r)} \right]{\vec e_y}$ (4)
${\vec E_t}(\vec r,t) = T\,{E_0}\,\exp \left[ {i(\omega t - {{\vec k}_t}\,.\,\vec r)} \right]{\vec e_y}$ (5)
ce qui définit les coefficients de réflexion R et de transmission T en amplitude.
I.A.1 Rappeler, sans les démontrer, les relations de passage du champ électromagnétique à la traversée du dioptre, qu'on exprimera pour $\vec E$ et $\vec B$.
I.A.2 En déduire les lois de la réflexion et de la réfraction de Snell-Descartes (on désignera par i' l'angle de réfraction).
I.A.3 Calculer R en fonction de n₁ , n₂ , i et i'.
I.A.4 On considère dans toute la suite que les indices n₁ et n₂ sont très proches, et on pose:
$n = {n_1} \approx {n_2}$ ,$\delta n = {n_2} - {n_1}$ et $\theta = \frac{\pi}{2 - i}$.
Montrer que le coefficient de réflexion s'écrit alors
$R = - \frac{{\delta n}}{{2n{{\sin }^2}(\theta )}}$ (6)
I.B
On se propose maintenant de montrer que l'onde réfléchie sur un dioptre en mouvement voit sa fréquence décalée par effet Doppler.
I.B.1 Le référentiel R étant associé au trièdre (Oxyz), on considère le référentiel R' en translation par rapport à R à la vitesse $ - V{\vec e_z}$ , auquel on associe le trièdre (O'xyz) avec $\overrightarrow {OO'} = - \,Vt{\vec e_z}$ .
La vitesse V est suffisamment faible devant la vitesse c de la lumière pour que l'on puisse négliger les effets relativistes et considérer que le champ électrique en un point M à l'instant t a la même valeur dans les deux référentiels R et R' .
Le champ électrique d'une onde s'écrit dans R :
$\vec E(\vec r,t) = {E_0}\exp \left[ {i(\omega t - \vec k\,.\,\vec r)} \right]{\vec e_y}$ (7)
Montrer que, dans R' , si l'on pose $\vec r' = \overrightarrow {O'M} $ , ce champ peut s'écrire:
$\vec E(\vec r',t) = {E_0}\exp \left[ {i(\omega 't - \vec k'\,.\,\vec r')} \right]{\vec e_y}$ (8)
et déterminer $\omega '$ et $\vec k'$ en fonction de ω , $\vec k$ et V .
I.B.2 Le dioptre considéré en (I.A.) est éclairé dans les mêmes conditions, mais il se translate maintenant à la vitesse $ - V{\vec e_z}$ , par rapport au référentiel R .
Montrer que, dans R , la pulsation ${\omega _r}$ de l'onde réfléchie est différente de la pulsation ${\omega _i}$ de l'onde incidente, et que le décalage $\Delta \omega = {\omega _r} - {\omega _i}$ vaut :
$\Delta \omega = \frac{{2nV\sin (\theta )}}{c}\omega $ (9)

I.C
Pour réaliser expérimentalement un dispositif permettant, sur ce principe, de décaler la fréquence d'une onde électromagnétique, on peut utiliser la propagation d'une onde acoustique dans un cristal. Une onde acoustique plane, de fréquence f et de longueur d'onde Λ , se propageant selon Oz dans la direction z < 0, induit une modulation de l'indice de réfraction du cristal autour d'une valeur moyenne n_c selon :
$n(z,t) = {n_c} + \Delta n\cos \left[ {2\pi \left( {ft + \frac{z}{\Lambda }} \right)} \right]$ (10)
avec $\Delta n > 0$ et $\Delta n < < {n_c}$. Tournez la page S.V.P.
Pour décrire l'interaction entre l'onde électromagnétique et l'onde acoustique, on adopte le modèle suivant, qui rend correctement compte des observations expérimentales. Le cristal est considéré comme une juxtaposition de petites tranches d'épaisseur $\delta z$ très inférieure à Λ , et donc d'indice pratiquement uniforme. Entre deux tranches successives, il y a un saut d'indice $\delta n = \frac{{\partial n}}{{\partial z}}\delta z$: chaque interface entre deux tranches élémentaires constitue un dioptre plan. Du fait de la propagation de l'onde acoustique, chacun de ces dioptres se déplace à vitesse $\vec V = - \,V{\vec e_z}$ constante.
Le cristal occupe la région de l'espace comprise entre les plans x = -e/2 et x = +e/2 ; on le suppose de grandes dimensions selon Oy et Oz . Le milieu extérieur, homogène, est d'indice n_a . Les faces x = -e/2 et x = +e/2 subissent un traitement anti-reflets : on considérera que les coefficients de transmission à travers ces faces sont égaux à 1.
On éclaire la face x = -e/2 du cristal par une onde plane, de champ électrique
${\vec E_i}(\vec r,t) = {E_0}\exp \left[ {i(\omega t - {{\vec k}_i}\,.\,\vec r)} \right]{\vec e_y}$ (11)
dont le vecteur d'onde ${\vec k_i}$ fait un angle ${\theta _a}$ avec ${\vec e_x}$.
L'amplitude Δn de la variation d'indice étant très faible devant n_c , l'onde réfractée dans le cristal s'y propage presque comme si l'indice était uniformément n_c , : elle est quasi plane, de vecteur d'onde ${\vec k_c}$ faisant avec ${\vec e_x}$ un angle ${\theta _c}$ d'amplitude pratiquement constante et égale à E₀. Cependant, chaque interface entre deux tranches élémentaires du cristal réfléchit une onde élémentaire, d'amplitude très faible devant E₀ (figure 1). Ces ondes élémentaires émergent du cristal en x = +e/2. Leur superposition, dans l'air, constitue l'onde réfléchie.

I.C.1 On considère un plan Σ orthogonal à la direction de l'onde réfléchie. Calculer, au niveau de Σ , le déphasage $\varphi ({z_i})$ entre l'onde élémentaire réfléchie par l'interface z = z_i et celle réfléchie en z = 0. On exprimera $\varphi ({z_i})$ en fonction de la longueur d'onde λ₀ dans le vide de l'onde incidente et on négligera évidemment pour ce calcul la célérité des ondes acoustiques devant celle de la lumière.
I.C.2 Les interfaces atteintes par l'onde incidente sont comprises entre z = -L/2 et z = +L/2. Montrer que l'amplitude complexe du champ total réfléchi peut se mettre sous la forme .
$\underset{\scriptscriptstyle-}{E}=K\exp (i\psi )\left\{ \exp \left[ i\alpha (t) \right]\text{sinc}\left[ \pi \text{L}\left( \frac{\text{1}}{\Lambda }-\frac{2{{n}_{a}}\sin ({{\theta }_{a}})}{{{\lambda }_{0}}} \right) \right]-\exp \left[ -i\alpha (t) \right]\text{sinc}\left[ \pi \text{L}\left( \frac{\text{1}}{\Lambda }+\frac{2{{n}_{a}}\sin ({{\theta }_{a}})}{{{\lambda }_{0}}} \right) \right] \right\}$
où K est un réel positif et $\psi $ un déphasage arbitraire dépendant du choix de Σ .
Préciser les expressions de K et α(t) en fonction des données.
I.C.3 Montrer que les deux termes contribuant à l'amplitude du champ réfléchi sont respectivement maximaux pour deux valeurs de ${\theta _a}$ opposées, notées respectivement ${\theta _B}$ et $ - {\theta _B}$ (angles de Bragg). On négligera pour cela la variation de K avec ${\theta _a}$ , et on justifiera a posteriori cette approximation, compte tenu des ordres de grandeur des différents paramètres
$L \approx 1mm$ $\Lambda \approx 50\mu m$ ${n_c} \approx 2$ ${\lambda _0} \approx 600nm$
Représenter l'allure de la variation avec sin(${\theta _a}$) de l'intensité lumineuse émergente.

I.C.4 Vérifier qu'à l'incidence de Bragg les ondes élémentaires réfléchies par l'interface en z = z_i et par celle en z = z_i + Λ interférent constructivement.
I.C.5 On envisage séparément ${\theta _a} = + {\theta _B}$ et${\theta _a} = - {\theta _B}$ représentés sur la figure 2 :

Montrer que l'onde optique réfléchie est décalée en fréquence de
$\frac{{\Delta \omega }}{{2\pi }} = \pm f$
avec un signe que l'on précisera pour chacune des deux configurations, et expliquer pourquoi ce décalage de fréquence est cohérent avec le résultat établi à la question (I.B.2).
Il Etude d'un dispositif expérimental
Un interféromètre de Mach-Zehnder, représenté sur la figure 3, est constitué de deux lames semi-transparentes identiques (L_E ) et (L_S ), et de deux miroirs de renvoi (M₁) et (M₂).
On éclaire la lame d'entrée (L_E) par le faisceau d'un laser hélium-néon, de longueur d'onde dans le vide λ₀ = 632, 8 nm et de pulsation $\omega = \frac{2\pi c}{{\lambda }_{0}}$.
Le faisceau transmis par (L_E ) traverse ensuite un modulateur acousto-optique, du type de celui étudié dans la première partie, dont l'effet est de décaler la fréquence du rayonnement. Ce modulateur est alimenté par un générateur de radiofréquences (R.F) , de fréquence f = 50 MHz, qui délivre un signal $m(t) = {m_0}\cos (2\pi \,ft)$ . Les ondes acoustiques produites ont ainsi la fréquence f . Comme on l'a montré dans la première partie, l'onde lumineuse émergeant du modulateur a alors pour pulsation $\omega + \Delta \omega $ , avec :
$\Delta \omega = 2\pi \,f$
Le faisceau est ensuite réfléchi sur (M₁ ) puis sur (L_S ). On désignera dans la suite par "bras de référence" le bras correspondant de l'interféromètre. Dans l'autre bras, que l'on appelera "bras de mesure", le faisceau réfléchi par (L_E) est ensuite réfléchi par (M₂) puis transmis par (Ls)
Tournez la page S.V.P.

L'interféromètre est réglé de telle façon que les deux faisceaux soient ensuite superposés au niveau d'un détecteur, qui délivre un signal électrique s(t) proportionnel à la puissance totale P(t) qu'il reçoit sur sa fenêtre d'entrée :
$s(t) = \eta P(t)$ (12)

II.A
La fenêtre d'entrée du détecteur est un carré de côté b, orthogonal à Oz et correspondant dans le plan Oxy à -b/2 < x < +b/2 et -b/2 < y < +b/2.
On désigne par ${\vec E_0}$ le champ électrique de l'onde provenant du bras de référence, et par ${\vec E_1}$ le champ provenant du bras de mesure. Au niveau du détecteur, ces deux champs s'écrivent :
${\vec E_0}(\vec r,t) = {E_0}\exp i\left[ {(\omega + \Delta \omega )t - {{\vec k}_0}\,.\,\vec r + {\varphi _0}} \right]{\vec e_y}$ (13)
${\vec E_1}(\vec r,t) = {E_1}\exp i\left[ {\omega t - {{\vec k}_1}\,.\,\vec r + {\varphi _1}} \right]{\vec e_y}$ (14)
On notera I₀ et I₁ les intensités correspondantes.
II.A.1 On suppose que les deux faisceaux émergeant de l'interféromètre sont parfaitement alignés, se propageant selon Oz. Calculer s(t) en fonction de I₀ et I₁ et montrer que l'on doit détecter un signal de battement à la fréquence f.
II.A.2 Du fait de l'inévitable imperfection du réglage de l'interféromètre, les faisceaux font en réalité entre eux un petit angle α , au niveau du détecteur. On considérera, par exemple, que l'un des faisceaux arrive sur la fenêtre sous incidence normale et l'autre sous incidence α . Que devient l'amplitude du signal de battement détecté ? Conclure.
II.A.3 La largeur de la fenêtre est b = 2 mm. Quelle valeur de l'angle α entre les deux faisceaux peut-on tolérer pour ne pas être gêné par le problème mis en évidence à la question précédente ? On supposera dans la suite que l'alignement est convenablement réalisé.
II.B
On cherche maintenant à mesurer l'amplitude du signal de battement à l'aide du dispositif électronique schématisé sur la figure 4, qui comprend deux multiplieurs analogiques et un filtre passe-bas de fréquence de coupure f_C .
Les signaux d'entrée du premier multiplieur sont le signal s(t) délivré par le photodétecteur et le signal de référence m(t) délivré par le générateur RF qui alimente aussi le modulateur.

II.B.1 Montrer qu'un choix judicieux de la valeur de f_c, permet d'obtenir un signal de sortie S₁ proportionnel à I₁ .
II.B.2 Le signal S₁ est très sensible aux perturbations extérieures, et peut varier simplement parce que l'on tapote un des miroirs de renvoi de l'interféromètre. Expliquer pourquoi.
Pour remédier à cet inconvénient, on produit un signal S₂ à l'aide d'un dispositif électronique parfaitement similaire, mais en remplaçant à l'entrée du premier multiplieur la référence m(t) par $m'(t) = {m_0}\sin (2\pi \,ft)$.
II.B.3 Comment peut-on, en pratique, obtenir le signal $m'(t)$ à partir du signal m(t) ?
II.B.4 Montrer que l'on peut effectivement, en utilisant S₁ et S₂ , produire un signal S qui ne soit plus aussi sensible aux perturbations extérieures et qui soit toujours proportionnel à I₁ .

II.C
On introduit dans le bras de mesure de l'interféromètre une cuve remplie d'une suspension de sphères de polystyrène microscopiques dans l'eau (figure 5). L'épaisseur de liquide traversée par le faisceau, dans la direction Oz , est D = 10 cm : la lumière pénètre dans la cuve en z = 0 et en ressort en z = D . L'indice de l'eau pour la longueur d'onde λ₀ est n_e = 1,33 ; celle du polystyrène n_p = 1,59. Chaque sphère diffuse la lumière, ce qui confère au liquide un aspect laiteux.
II.C.1 Expliquer pourquoi on n'attend pas, au niveau du détecteur, de signal de battements entre la lumière diffusée par la cuve et le faisceau de référence.
Quel problème de cohérence se pose-t-il ici ? On pourra s'appuyer sur les résultats de (II.A).
On observe cependant un phénomène de battements, mais il correspond aux interférences entre le faisceau de référence et la partie de la lumière qui a traversé la cuve en ligne droite et émerge dans la direction d'incidence. On appelle intensité cohérente I_C l'intensité lumineuse correspondant à cette lumière. Le signal S permet de mesurer directement l'intensité cohérente I_C à la sortie de la cuve.
Tournez la page S.V.P.

II.C.2 Montrer que, à l'intérieur de la cuve, I_C est fonction de z et vérifie l'équation :
$\frac{{d\,{I_c}(z)}}{{dz}} = - v\,{\sigma _d}\,{I_c}(z)$ (15)
où v est le nombre de sphères par unité de volume et ${\sigma _d}$ la section efficace de diffusion, définie comme le rapport entre la puissance P_d diffusée par une sphère et l'intensité incidente I_c sur cette sphère :
${\sigma _d} = \frac{{{P_d}}}{{{I_c}}}$ (16)
En déduire que l'intensité cohérente I_c(D) à la sortie de la cuve vérifie :
${I_c}(d) = {I_{c0}}\exp ( - v{\kern 1pt} {\sigma _d}{\kern 1pt} D)$ (17)
Que représente ${I_{c0}}$ ?
II.C.3 Le tableau 1 donne les valeurs expérimentales de $\ln \left[ {\frac{{{I_c}(D)}}{{{I_{c0}}}}} \right]$ mesurées pour différentes
valeurs de la fraction volumique de polystyrène, c'est-à-dire du rapport entre le volume de polystyrène et le volume total de la solution :

Commenter ces valeurs numériques.
La section efficace de diffusion ${\sigma _d}$ est fonction de n_e , n_p , λ₀ et du volume V des sphères:
${\sigma _d} = 24{\pi ^3}{\left( {\frac{{{n_e}}}{{{\lambda _0}}}} \right)^4}{\left( {\frac{{n_p^2 - n_e^2}}{{n_p^2 + 2n_e^2}}} \right)^2}{V^2}$ (18)
Déterminer le rayon a des sphères utilisées.
II.C.4 Les incertitudes relatives sur les mesures des intensités sont de 1 % ; celles sur les fractions volumiques de 0,5 %. Evaluer l'incertitude Δa sur le rayon des sphères.
III Diffusion de la lumière par une particule sphérique
Dans cette partie, on se propose de justifier l'expression de la section efficace de diffusion ${\sigma _{\rm{d}}}$ utilisée à la question (II.C.3).

III.A
On considère une sphère, de rayon a , de polarisation $\vec P$ uniforme, dans le vide. On veut calculer le champ électrostatique créé par cette distribution de polarisation.
III.A.1 Montrer que le champ créé par la polarisation $\vec P$ est identique à celui que créerait une distribution surfacique de charges ${\sigma _{{\rm{lié }}}}$ , que l'on précisera.
III.A.2 Montrer que l'on peut retrouver cette distribution surfacique de charges en superposant deux sphères de même rayon a , uniformément chargées, de densité volumique de charge respectivement + ρ et - ρ, centrées en deux points infiniment voisins, respectivement O₊ et O_- Etablir la relation liant $\vec P$, ρ , O₊ et O_- .
III.A.3 Donner l'expression du potentiel électrostatique V_ρ créé en tout point M de l'espace par une sphère de rayon a et de centre O, de densité de charge uniforme ρ . On prendra le potentiel nul lorsque M est à l'infini.
III.A.4 Déduire des résultats précédents l'expression du potentiel ${V_{\vec P}}$ à l'intérieur de la sphère uniformément polarisée; montrer que le champ ${\vec E_{\vec P}}$ orrespondant est uniforme et vaut :
${\vec E_{\vec P}} = - \frac{{\vec P}}{{3{\varepsilon _0}}}$ (19)
III.B
On considère maintenant une sphère de polystyrène, de rayon a et de centre O , dans le vide. Le polystyrène est un matériau isotrope, d'indice de réfraction n_P ; on notera ε_p sa permittivité diélectrique absolue.
On envoie sur la sphère une onde électromagnétique plane, monochromatique de pulsation ω, de champ électrique :
${\vec E_i}(\vec r,t) = {\vec E_{i0}}\exp \left[ {i(\omega t - \vec k\,.\,\vec r)} \right]$ (20)
On cherche à déterminer le champ électromagnétique $({\vec E_d},{\vec B_d})$ diffusé par la sphère, et défini par les relations :
$\vec E = {\vec E_i} + {\vec E_d}$ et $\vec B = {\vec B_i} + {\vec B_d}$ (21)
où $(\vec E,\vec B)$ représente le champ électromagnétique total et $({\vec E_i},{\vec B_i})$ le champ incident.

III.B.1 On note $({\vec E^{{\mathop{\rm int}} }},{\vec B^{{\mathop{\rm int}} }})$ et $({\vec E^{{\rm{ext}}}},{\vec B^{{\rm{ext}}}})$ les champs respectivement à l'intérieur et à l'extérieur de la sphère.
Ecrire les équations de Maxwell pour ces champs.
III.B.2 Exprimer les relations de passage vérifiées par $\vec E$ et $\vec B$ à la surface de la sphère.
III.B.3 Vérifier que, à l'extérieur de la sphère, le champ diffusé $({\vec E_d},{\vec B_d})$ vérifie simplement les équations de Maxwell dans le vide.
Tournez la page S.V.P.
III.B.4 Montrer que, à l'intérieur de la sphère, le champ diffusé vérifie aussi les équations de Maxwell dans le vide, à condition d'y introduire une distribution volumique de courant ${\vec j_{{\rm{lié }}}}$ dont on exprimera l'amplitude complexe ${{\underset{\scriptscriptstyle-}{\vec{j}}}_{\text{li }\!\!\acute{\mathrm{e}}\!\!\text{ }}}$ en fonction de celle du champ total ${\vec E^{{\mathop{\rm int}} }}$ à l'intérieur de la sphère.
III.B.5 Montrer qu'on peut alors considérer le champ diffusé comme le champ créé dans le vide par la distribution de courant ${\vec j_{{\rm{li\'e }}}}$ à condition de rajouter une distribution surfacique de charges ${\sigma _{{\rm{li\'e }}}}$ que l'on déterminera.
III.B.6 Montrer enfin que le champ créé par cette distribution de charges et de courants est équivalent au champ qui serait créé par une sphère polarisée, de polarisation :
$\vec P = ({\varepsilon _p} - {\varepsilon _0}){\vec E^{{\mathop{\rm int}} }}$ (22)
III.C
On introduit le potentiel scalaire V_d et le potentiel vecteur ${\vec A_{\rm{d}}}$ associés au champ diffusé $({\vec E_d}\,,\,{\vec B_d})$.
On impose à ces potentiels de vérifier, en tout point de l'espace, la condition de jauge de Lorentz :
${\rm{div}}\,({\vec A_{\rm{d}}}) + \frac{1}{{{c^2}}}\frac{{\partial {V_{\rm{d}}}}}{{\partial {\rm{t}}}} = 0$ (23)
On montre, à l'aide des équations de Maxwell, que ${{\underset{\scriptscriptstyle-}{\vec{A}}}_{\text{d}}}$ satisfait l'équation
$\Delta \,{{\vec{A}}_{\text{d}}}+{{\mu }_{0}}{{\varepsilon }_{0}}{{\omega }^{2}}{{\vec{A}}_{\text{d}}}=-{{\mu }_{0}}{{\underset{\scriptscriptstyle-}{\vec{j}}}_{\text{li }\!\!\acute{\mathrm{e}}\!\!\text{ }}}$ (24)
dont la solution est :
${{\underset{\scriptscriptstyle-}{\vec{A}}}_{\text{d}}}(\vec{r})=\frac{{{\mu }_{0}}}{4\pi }\iiint_{\text{espace}}{{{{\underset{\scriptscriptstyle-}{\vec{j}}}}_{\text{li }\!\!\acute{\mathrm{e}}\!\!\text{ }}}}(\vec{r}')\frac{\exp (-ik\left\| \vec{r}-\vec{r}' \right\|}{\left\| \vec{r}-\vec{r}' \right\|}{{d}^{3}}r'$ (25)
où k est le nombre d'onde défini par $k = \frac{2 \pi }{\lambda _{0}} = \frac{\omega}{c}$ . La notation d³ r', représente un volume élémentaire autour du point M' tel que $\overrightarrow {OM'} = \vec r'$ .
III.C.1 Cette solution est appelée solution des potentiels retardés. Pourquoi ?
On a vu en (III.B.4.) que ${\vec j_{{\rm{lié }}}}$ était fonction de $\vec E$ , lequel n'est pas connu a priori puisqu'il dépend de ${\vec E_{\rm{d}}}$ qui dépend lui-même de ${\vec A_{\rm{d}}}$ ... La résolution dans le cas général apparaît donc délicate.
On se limite dans toute la suite au cas particulier plus simple où la sphère est de rayon très petit devant la longueur d'onde du rayonnement : a << λ₀ . Cette restriction permet, entre autres, de considérer que le champ incident est pratiquement uniforme à l'intérieur de la sphère. Il est alors tentant de chercher, pour $\vec E$ et ${\vec E_{\rm{d}}}$ une solution correspondant à une polarisation $\vec P$ uniforme dans le volume de la sphère. Il faudra évidemment ensuite vérifier à posteriori la compatibilité de la solution obtenue avec cette hypothèse.

III.C.2 Montrer que, dans ces conditions, l'intégrale permettant le calcul de ${{\underset{\scriptscriptstyle-}{\vec{A}}}_{\text{d}}}^{\operatorname{int}}$ a la même forme
que celle correspondant au potentiel électrostatique créé par une sphère uniformément chargée. En déduire l'expression de ${{\underset{\scriptscriptstyle-}{\vec{A}}}_{\text{d}}}^{\operatorname{int}}$ .
III.C.3 Calculer ${{\underset{\scriptscriptstyle-}{V}}_{\text{d}}}^{\operatorname{int}}$ puis les amplitudes complexes ${{\vec{\underset{\scriptscriptstyle-}{E}}}_{\text{d}}}^{\operatorname{int}}$ et ${{\underset{\scriptscriptstyle-}{\vec{B}}}_{\text{d}}}^{\operatorname{int}}$ des champs diffusés.
III.C.4 Exprimer ${\vec E_{\rm{d}}}^{{\mathop{\rm int}} }$ et ${\vec B_{\rm{d}}}^{{\mathop{\rm int}} }$ en fonction du champ incident ${\vec E_i}$ .
Cette solution est-elle cohérente avec l'hypothèse d'uniformité de $\vec P$ ?
IILD
On cherche maintenant à déterminer le champ ${\vec E_{\rm{d}}}$ diffusé en un point M situé à une distance r de la sphère de polystyrène très grande devant la longueur d'onde : r >> λ₀ .
III.D.1 Montrer que la solution des potentiels retardés peut alors s'écrire :
 ${{\underset{\scriptscriptstyle-}{\vec{A}}}_{\text{d}}}(\vec{r})={{\underset{\scriptscriptstyle-}{\vec{A}}}_{0}}\frac{\exp (-ikr)}{r}$ (26)
ou ${{\underset{\scriptscriptstyle-}{\vec{A}}}_{0}}$ est une constante vectorielle que l'on exprimera en fonction de a et ${{\underset{\scriptscriptstyle-}{\vec{j}}}_{\text{li }\!\!\acute{\mathrm{e}}\!\!\text{ }}}$ .
III.D.2 Pour repérer la position du point M , on introduit le système de coordonnées sphériques de pôle O et d'axe polaire Oz , tel que ${{\underset{\scriptscriptstyle-}{\vec{A}}}_{0}}={{A}_{0}}\,{{\vec{e}}_{z}}$ . On a ainsi $\theta = ({\vec A_0},\vec r)$ . Etablir les expressions de ${{\underset{\scriptscriptstyle-}{V}}_{\text{d}}}$ et ${{\underset{\scriptscriptstyle-}{\vec{E}}}_{\text{d}}}$ en projection sur la base $({\vec e_r},\,{\vec e_\theta },\,{\vec e_\varphi })$ associée.
IILD.3 Montrer qu'au voisinage de $\vec r = {\vec r_0}$ , le champ ${\vec E_{\rm{d}}}$ a pratiquement une structure d'onde plane (on posera $\vec r = {\vec r_0} + \vec \delta $) . En déduire que l'intensité moyenne (puissance surfacique moyenne) diffusée dans la direction de $\vec r$ est proportionnelle à ${{\left\| {{{\underset{\scriptscriptstyle-}{\vec{E}}}}_{\text{d}}} \right\|}^{2}}$ avec un coefficient de proportionnalité que l'on exprimera en fonction de c et ε₀ .

IILD.4 Déduire du résultat précédent la puissance moyenne totale ${P_d}$ diffusée par la sphère en fonction de A₀ .
III.D.5 En utilisant les relations démontrées en (III.D.1), (III.B.4) et (III.C.4), exprimer ${P_d}$ en fonction de ${{\left\| {{{\underset{\scriptscriptstyle-}{\vec{E}}}}_{i}} \right\|}^{2}}$ .
IILD.6 Exprimer l'intensité I_i du champ incident en fonction de ${{\left\| {{{\underset{\scriptscriptstyle-}{\vec{E}}}}_{i}} \right\|}^{2}}$ . On définit la section efficace de diffusion ${\sigma _{\rm{d}}}$ par :
${P_d} = {\sigma _{\rm{d}}}\,{I_i}$ (27)
Montrer que, si V représente le volume de la sphère de polystyrène, on a:
${\sigma _{\rm{d}}} = 24{\pi ^3}\frac{1}{{\lambda _0^4}}{\left( {\frac{{{\varepsilon _p} - {\varepsilon _0}}}{{{\varepsilon _p} + 2{\varepsilon _0}}}} \right)^2}\,{V^2}$ (28)
IILD.7 Comparer le résultat obtenu à l'expression de ${\sigma _{\rm{d}}}$ donnée en (ILC.3).