A 94 PHYS. I - M, P’
ÉCOLE NATIONALE DES PONTS ET CHAUSSÉES,
ÉCOLES NATIONALES SUPÉRIEURES DE L'AÉRONAUTIQUE ET DE L'ESPACE,
DE TECHNIQUES AVANCÉES, DES TÉLÉCOMMUNICATIONS,
DES MINES DE PARIS, DES MINES DE SAINT-ÉTIENNE, DES MINES DE NANCY,
DES TÉLÉCOMMUNICATIONS DE BRETAGNE,
ÉCOLE POLYTECHNIQUE (OPTION T.A.)
CONCOURS D'ADMISSION 1994
PHYSIQUE
PREMIÈRE ÉPREUVE
OPTIONS M et P'
(Durée de l'épreuve : 3 heures)
Les candidats sont priés de mentionner de façon apparente sur la première page de la copie : PHYSIQUE I.
L'énoncé de cette épreuve, commune aux candidats des options M et P', comporte 6 pages.
L’épreuve est constituée de deux problèmes indépendants entre eux et que l’on pourra aborder dans l’ordre qu’on voudra.
On étudie dans ce problème le fonctionnement et la mise en œuvre de circuits présentant le phénomène de résistance différentielle négative, c’est-à-dire tels que le rapport $r = \frac{\Delta e}{\Delta i}$ des petites variations de tension et de courant autour d’un point de repos soit négatif. Les amplificateurs opérationnels AO (fig.1a) intervenant dans les divers montages auront des courants d’entrée ${i_1}$ et ${i_2}$ nuls et leur impédance d’entrée sera considérée comme infinie.
fig.1 a : Notations pour AO fig. 1b : Circuit pouvant exhiber $r = \frac{\Delta e}{\Delta i}<0$
Première partie : Réalisation de circuits d’impédance différentielle négative
On considère d’abord que le gain des amplificateurs est infini ; dans ces conditions, le régime linéaire de fonctionnement se caractérise par ${V_1} = {V_2}$ ; autrement, la tension de sortie est
${V_s} = signe\left( {{V_2} - {V_1}} \right) \times E$ (régime dit de saturation,$E = 15V$ = tension de saturation ).
I -1) Déterminer la relation $i\left( e \right)$ dans le circuit de la figure 1b, d’abord en régime linéaire, puis en régime de saturation. Pour quelles inégalités portant sur $e$ ce dernier régime est-il possible (distinguer les cas ${V_s} = \pm E$) ?
I -2) Représenter le graphe complet de la relation $i\left( e \right)$ lorsque ${R_0} < R$, en précisant les points particuliers et les différents domaines de fonctionnement.
On considère maintenant que la tension de sortie des amplificateurs opérationnels s’exprime en fonction de la tension d’entrée par ${V_s} = A\left( {{V_2} - {V_1}} \right)$, où $A$ est un nombre réel très grand devant 1. Les relations entre tensions et courants dans le circuit représenté sur la figure 2a (redessinée en 2b) sont linéaires et peuvent donc s’écrire, avec les conventions habituelles relatives aux grandeurs complexes décrivant le régime harmonique : $\begin{array}{l}\underline {{I_1}} = \underline {{Y_{11}}} \,\underline {{V_1}} + \underline {{Y_{12}}} \,\underline {{V_2}} \\\underline {{I_2}} = \underline {{Y_{21}}} \,\underline {{V_1}} + \underline {{Y_{22}}} \,\underline {{V_2}} \end{array}$, soit, en notation matricielle : $\left[ {\begin{array}{*{20}{c}}{\underline {{I_1}} }\\{\underline {{I_2}} }\end{array}} \right] = \left[ {\underline Y } \right]\,\left[ {\begin{array}{*{20}{c}}{\underline {{V_1}} }\\{\underline {{V_2}} }\end{array}} \right]$. La matrice $\left[ {\underline Y } \right]$ ainsi introduite s’appelle matrice admittance.
fig. 2a : Un circuit à AO fig. 2b : Circuit 2a, présenté comme un quadripôle
Remarquer que les courants sont comptés positivement quand ils entrent dans le quadripôle.
I-3) Calculer la matrice$\left[ {\underline Y } \right]$ relative au circuit considéré.
I-4) Quelle est, dans le cas général, la matrice $\left[ {\underline Y } \right]$ relative à deux quadripôles de matrices admittances respectives $\left[ {\underline {Y\,'} } \right]$ et $\left[ {\underline {Y\,''} } \right]$, montés en parallèle (c’est-à-dire en reliant ensemble leurs bornes homologues) ?
I-5) Calculer, pour le circuit de la fig. 2, la matrice $\left[ {\underline M } \right]$ définie par $\left[ {\begin{array}{*{20}{c}}{\underline {{V_2}} }\\{\underline {{I_2}} }\end{array}} \right] = \left[ {\underline M } \right]\left[ {\begin{array}{*{20}{c}}{\underline {{V_1}} }\\{\underline {{I_1}} }\end{array}} \right]$. Que devient cette relation lorsque $A$ tend vers l’infini ? Quelle relation existe-t-il alors entre les grandeurs réelles ${V_1}$ et ${V_2}$ d’une part, ${i_1}$ et ${i_2}$ d’autre part ?
I-6) Soit $\underline {{Z_1}} $ l’impédance d’entrée du montage précédent, c’est-à-dire, comme indiqué à la figure 3a, l’impédance du dipôle entre la masse et la borne (1), lorsque l’on place une charge d’impédance complexe entre la masse et la borne (2). Soit de même$\underline {{Z_2}} $ l’impédance de sortie du montage de la figure 3b. Exprimer $\underline {{Z_1}} $ et $\underline {{Z_2}} $ en fonction de ${R_1},{R_2}$ et $Z$.
fig. 3a : Montage pour $\underline {{Z_1}} $ d’un quadripôle fig. 3b: Montage pour $\underline {{Z_2}} $ d’un quadripôle
I-7) On pose $K = \frac{{{R_1}}}{{{R_2}}}$. Donner l’expression des impédances $\underline {{Z_1}} $ et $\underline {{Z_2}} $ en fonction de $K$ dans les deux cas suivants : $\underline Z = R$ d’une part, $\underline Z = \frac{1}{{jC\omega }}$ d’autre part, impédance capacitive.
Deuxième partie : Réalisation d’un gyrateur
Un gyrateur est un quadripôle travaillant en régime linéaire sinusoïdal dont la matrice admittance s’écrit :$\left[ {\begin{array}{*{20}{c}}{\underline {{I_1}} }\\{\underline {{I_2}} }\end{array}} \right] = \left[ {\begin{array}{*{20}{c}}0&{ - \frac{Y}{a}}\\{aY}&0\end{array}} \right]\,\left[ {\begin{array}{*{20}{c}}{\underline {{V_1}} }\\{\underline {{V_2}} }\end{array}} \right]$. Les courants sont comptés positivement lorsqu’ils entrent dans le quadripôle, $Y$ est une admittance réelle positive et $a$ est un réel positif.
II-1) Quel est le rapport entre la puissance moyenne sortante et la puissance moyenne entrante ?
II-2) En déduire qu’un gyrateur fermé sur un composant qui ne consomme pas de puissance simule à l’entrée un composant qui ne consomme pas non plus de puissance.
II-3) Que peut-on dire du quadripôle si $a$ est strictement plus grand que l’unité ?
II-4) Exprimer$\underline {{Z_1}} $ , impédance d’entrée du gyrateur, en fonction de$\underline {{Z_u}} $ impédance placée en sortie. Préciser ces expressions lorsque le quadripôle est fermé sur une inductance $L$, ou sur une capacité $C$. C’est plutôt sous cette dernière forme que le gyrateur est généralement utilisé. Quelle en est, selon vous, la raison ?
II-5) On considère que dans le schéma de la figure 4, l’amplificateur fonctionne en régime linéaire. Déterminer la relation entre ${R_1},\;{R_2},\;{R_3}$ et ${R_4}$ pour que la matrice admittance du quadripôle ainsi formé soit : $\left[ {\begin{array}{*{20}{c}}{\frac{1}{{{R_1}}}}&{ - \frac{1}{{{R_1}}}}\\{\frac{1}{{{R_4}}}}&0\end{array}} \right]$.
fig. 4 : Schéma de la question II-5) fig. 5 : Une réalisation de gyrateur (question II-9))
II-6) Représenter par ses éléments un quadripôle dont la matrice admittance est : $\left[ {\begin{array}{*{20}{c}}{\frac{1}{{{R_1}}}}&0\\0&0\end{array}} \right]$.
II-7) Représenter par ses éléments un quadripôle dont la matrice admittance est : $\left[ {\begin{array}{*{20}{c}}{ - \frac{1}{{{R_1}}}}&0\\0&0\end{array}} \right]$. On utilisera à cet effet un amplificateur opérationnel, deux résistors de même résistance$R$ et un résistor de résistance ${R_1}$.
II-8) Comment brancher le quadripôle déterminé à la question II-7) sur celui de la fig. 4 pour obtenir un gyrateur ?
II-9) Avec le moins de calculs possibles, montrer que le schéma de la fig. 5 réalise un gyrateur et, toujours dans le cadre d’un régime de fonctionnement linéaire, donner les valeurs de $Y$ et de $a$ qui lui sont associées.
Troisième partie : Utilisation du gyrateur
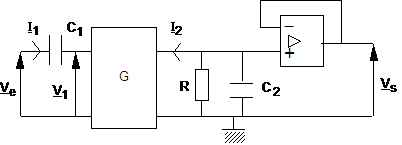
III-1) La fig. 6 représente le gyrateur G de la fig. 5 fermé sur l’association de $R$ et ${C_2}$ montés en parallèle . Déterminer l’expression de la transmittance $\frac{\underline{{{V}_{s}}}}{\underline{{{V}_{e}}}}$du filtre ainsi réalisé (on pourra poser $\omega _0^2 = \frac{1}{{R_1^2{C_1}{C_2}}}$ et $Q = R{C_2}{\omega _0}$). Qu’a-t-on ainsi simulé ?
fig. 6 Filtre accordable utilisant un gyrateur
III-2) Quel est le rôle de l’amplificateur opérationnel en fin de montage ?
III-3) Donner l’expression de la fréquence d’accord, de la largeur de bande passante et du facteur de qualité de ce filtre, en fonction de la valeur de ses composants. Montrer que les réglages de la bande passante et de la fréquence d’accord sont indépendants l’un de l’autre.
FIN DE CE PROBLÈME
Première partie : Superposition d’écoulements
On considère l’écoulement d’un fluide incompressible parfait défini par le champ de vitesse ${\vec V_1} = \frac{\lambda }{{2\pi {r_1}}}{\vec u_1}$, où $\lambda $ est une constante réelle et ${r_1},\;{\theta _1}$ et $z$ les coordonnées cylindriques d’un point M par rapport au point A1 de coordonnées $\left( { - a,\;0,\;0} \right)$ dans un repère galiléen $\left( {O,\;x,\;y,\;z} \right)$ muni de la base orthonormée $\left( {\vec x,\;\vec y,\;\vec z} \right)$. Le point $H$ (fig. 1) étant la projection du point M sur le plan $\left( {xOy} \right)$, on a : $\vec{A_{1}M}= {r_1}{\vec u_1} + z\vec z$, où ${\vec u_1}$est le vecteur unitaire porté par $vec{A_{1}H}$.
I-1) Montrer que la circulation du vecteur ${\vec V_1}$ entre deux points A et B est indépendante du chemin suivi et déterminer le potentiel $\varphi {'_1}\left( {{r_1}} \right)$ associé à cet écoulement $\left( {{{\vec V}_1} = + {\bf{grad}}\left( {\varphi _1^{'}} \right)} \right)$, sachant qu’il est par convention nul pour une certaine valeur ${r_0}$ de ${r_1}$.
I-2) Cet écoulement suit-il la loi de Laplace $\Delta \varphi _1^{'} = 0$?
fig. 1 : Écoulement défini par ${\vec V_1} = \frac{\lambda }{{2\pi {r_1}}}{\vec u_1}$ fig. 2 : Écoulement défini par ${\vec V_1} + {\vec V_2}$(cf. I-3))
I-3) On superpose à l’écoulement précédent le nouvel écoulement défini par le champ de vitesse ${\vec V_2} = \frac{{ - \lambda }}{{2\pi {r_2}}}{\vec u_2}$, avec $\vec{A_{2}M}= \vec{A_{2}H}+ \vec{HM}={r_2}{\vec u_2} + z\vec z$ (fig. 2), les coordonnées du point A2 étant $\left( {a,\;0,\;0} \right)$. Quelle est l’expression du potentiel des vitesses ${\varphi _1}\left( {{r_1},\;{r_2}} \right)$ associé à l’écoulement résultant, l’origine des potentiels étant prise dans le plan $\left( {yOz} \right)$ ?
I-4) On fait tendre $a$ vers 0 et $\lambda $ vers l’infini, de telle sorte que le produit $2\lambda a=M$soit constant. Montrer que le potentiel en coordonnées cylindriques (vecteurs unitaires ${\vec u_r}$ et ${\vec u_\theta }$) s’écrit alors ${{\varphi }_{1}}=\frac{M\cos \theta }{2\pi r}$, où $\theta $ est l’angle entre $Ox$ et $OH$ (voir fig. 2).
I-5) Déterminer l’équation des lignes de courant ; tracer rapidement leur allure.
I-6) On superpose à cet écoulement un écoulement uniforme, de vitesse $\vec u = u\vec x$. Montrer qu’il existe pour l’écoulement résultant une ligne de courant circulaire d’axe $Oz$, dont on précisera le rayon $R$ en fonction de $M$ et de $u$. Donner alors, qualitativement, la forme des lignes de courant ; on distinguera les cas $r$<$R$ et $r$>$R$.
I-7) Un cylindre rigide immobile de rayon $R$ est immergé dans le fluide. La vitesse du fluide pour $r$ très grand devant $R$ est uniforme et égale à $\vec u = u\vec x$. Montrer qu’à l’extérieur du cylindre le régime d’écoulement trouvé en I-6) est solution du problème en présence du cylindre. Existe-t-il des points de vitesse nulle ? Quel est le potentiel ${\varphi _t}$ de l’écoulement ? Voyez-vous une analogie, magnétostatique ou électrostatique, à ce problème d’écoulement ?
I-8) On superpose enfin un dernier écoulement, défini par la vitesse ${\vec V_3}$ pour $r$>$R$: ${\vec V_3} = \frac{C}{{2\pi r}}{\vec u_\theta }$, où $C$ est une constante. Montrer que cet écoulement dérive d’un potentiel ${\varphi _3}$, dont on ne demande pas d’établir l’expression. Quelle est la circulation du vecteur ${\vec V_3}$ sur une courbe fermée dans les deux cas où l’origine est à l’intérieur ou à l’extérieur de la courbe ? Voyez-vous une analogie, magnétostatique ou électrostatique, à ce problème d’écoulement ?
Deuxième partie : Voile de Flettner
Un bateau est muni d’un cylindre vertical de rayon $R$ et de hauteur $h$, tournant autour d’un axe vertical à la vitesse angulaire $\vec \omega = \omega \vec z$. Le vent souffle avec une vitesse uniforme constante $\vec u = u\vec x$. L’écoulement de potentiel des vitesses ${\varphi _t}$ de la question I-7) correspond à l’écoulement du vent autour du cylindre de rayon $R$, satisfaisant aux conditions aux limites. L’écoulement de potentiel des vitesses ${\varphi _3}$ de la question I-8) correspond à l’effet d’entraînement de l’air (de masse volumique $\rho $) par la rotation du cylindre.
II-1) Donner la relation entre la constante $C$ et $\omega $. On remarquera que, dans ce modèle, la vitesse du vent sur le cylindre est celle du cylindre, autrement dit que la vitesse tangentielle ne s’annule pas sur la paroi du cylindre (ce point relève, en fait, de la viscosité) .
II-2) Calculer, en coordonnées polaires, les composantes de la vitesse résultante pour $r$>$R$.
II-3) Sachant que, loin du bateau, le vent n’est pas perturbé et que la pression est égale à la pression atmosphérique normale ${p_c}$, déterminer, en fonction de l’angle $\theta $, la pression autour du cylindre ($r$=$R$).
II-4) Quelle est, en fonction de $R$, $C$, $\vec u$, $\vec z$ et de la masse volumique de l’air $\rho $, la résultante des forces de pression par unité de hauteur sur le cylindre ? On pourra aussi bien exprimer le résultat en fonction de $R$, $\rho $, $\vec u$ et $\vec \omega $.
II-5) Préciser sur un schéma le sens de rotation du cylindre correspondant à une force propulsive. Quelle est l’allure du vent la plus favorable (vent de près, vent de travers et vent arrière sont précisés sur la figure 3-a).
fig. 3a : Allures du vent fig. 3b : Voile classique et vent (cf. II-7)) fig. 3c : Bordage optimal
II-6) La vitesse du vent est $10$m.s-1 ; la masse volumique de l’air est $1,3$ kg.m-3. Le cylindre a une hauteur de $10$m et un rayon de $30$cm ; $\omega = 30\;{\rm{rad}}{\rm{.}}{{\rm{s}}^{ - {\rm{1}}}}$. Calculer la valeur numérique maximale de la force propulsive.
Troisième partie : Comparaison avec une voile classique
III-1) Une voile plane d’aire $\Sigma $ et de vecteur unitaire normal $\vec \sigma $ reçoit une veine de vent de vitesse $\vec u$ sous l’angle $\alpha $ et la réfléchit selon la loi de Descartes (fig. 3-b). Quel est le vecteur force exercé par le vent sur la voile ? On pourra introduire le débit $D = \rho \Sigma u\sin \alpha $.
III-2) Le bateau reçoit le vent par le travers (fig. 3-c), l’axe du bateau est perpendiculaire au vent relatif. Quelle est dans ces conditions, en fonction de $\rho $, $u$, $\Sigma $ et $\alpha $ la composante propulsive de la force précédente ?
III-3) Pour quelle valeur de $\alpha $ cette composante est-elle maximale ? De quel type de vent s’agit-il ? Calculer numériquement la force propulsive maximale avec le même vent qu’en II-6) ($u = 10\,{\rm{m}}{\rm{.}}{{\rm{s}}^{ - {\rm{1}}}},\;\rho = 1,3\,{\rm{kg}}{\rm{.}}{{\rm{m}}^{ - {\rm{3}}}}$) pour une voile de $25$m2. Comparer avec le cylindre de Flettner (le maximum de la fonction $\left( {{{\sin }^2}\alpha } \right)\cos \alpha $ vaut $0,385$).
FIN DE CE PROBLÈME
ÉCOLE NATIONALE DES PONTS ET CHAUSSÉES,
ÉCOLES NATIONALES SUPÉRIEURES DE L'AÉRONAUTIQUE ET DE L'ESPACE,
DE TECHNIQUES AVANCÉES, DES TÉLÉCOMMUNICATIONS,
DES MINES DE PARIS, DES MINES DE SAINT-ÉTIENNE, DES MINES DE NANCY,
DES TÉLÉCOMMUNICATIONS DE BRETAGNE,
ÉCOLE POLYTECHNIQUE (OPTION T.A.)
CONCOURS D'ADMISSION 1994
PHYSIQUE
PREMIÈRE ÉPREUVE
OPTIONS M et P'
(Durée de l'épreuve : 3 heures)
Les candidats sont priés de mentionner de façon apparente sur la première page de la copie : PHYSIQUE I.
L'énoncé de cette épreuve, commune aux candidats des options M et P', comporte 6 pages.
L’épreuve est constituée de deux problèmes indépendants entre eux et que l’on pourra aborder dans l’ordre qu’on voudra.
On étudie dans ce problème le fonctionnement et la mise en œuvre de circuits présentant le phénomène de résistance différentielle négative, c’est-à-dire tels que le rapport $r = \frac{\Delta e}{\Delta i}$ des petites variations de tension et de courant autour d’un point de repos soit négatif. Les amplificateurs opérationnels AO (fig.1a) intervenant dans les divers montages auront des courants d’entrée ${i_1}$ et ${i_2}$ nuls et leur impédance d’entrée sera considérée comme infinie.
Première partie : Réalisation de circuits d’impédance différentielle négative
On considère d’abord que le gain des amplificateurs est infini ; dans ces conditions, le régime linéaire de fonctionnement se caractérise par ${V_1} = {V_2}$ ; autrement, la tension de sortie est
${V_s} = signe\left( {{V_2} - {V_1}} \right) \times E$ (régime dit de saturation,$E = 15V$ = tension de saturation ).
I -2) Représenter le graphe complet de la relation $i\left( e \right)$ lorsque ${R_0} < R$, en précisant les points particuliers et les différents domaines de fonctionnement.
On considère maintenant que la tension de sortie des amplificateurs opérationnels s’exprime en fonction de la tension d’entrée par ${V_s} = A\left( {{V_2} - {V_1}} \right)$, où $A$ est un nombre réel très grand devant 1. Les relations entre tensions et courants dans le circuit représenté sur la figure 2a (redessinée en 2b) sont linéaires et peuvent donc s’écrire, avec les conventions habituelles relatives aux grandeurs complexes décrivant le régime harmonique : $\begin{array}{l}\underline {{I_1}} = \underline {{Y_{11}}} \,\underline {{V_1}} + \underline {{Y_{12}}} \,\underline {{V_2}} \\\underline {{I_2}} = \underline {{Y_{21}}} \,\underline {{V_1}} + \underline {{Y_{22}}} \,\underline {{V_2}} \end{array}$, soit, en notation matricielle : $\left[ {\begin{array}{*{20}{c}}{\underline {{I_1}} }\\{\underline {{I_2}} }\end{array}} \right] = \left[ {\underline Y } \right]\,\left[ {\begin{array}{*{20}{c}}{\underline {{V_1}} }\\{\underline {{V_2}} }\end{array}} \right]$. La matrice $\left[ {\underline Y } \right]$ ainsi introduite s’appelle matrice admittance.
Remarquer que les courants sont comptés positivement quand ils entrent dans le quadripôle.
I-3) Calculer la matrice$\left[ {\underline Y } \right]$ relative au circuit considéré.
I-4) Quelle est, dans le cas général, la matrice $\left[ {\underline Y } \right]$ relative à deux quadripôles de matrices admittances respectives $\left[ {\underline {Y\,'} } \right]$ et $\left[ {\underline {Y\,''} } \right]$, montés en parallèle (c’est-à-dire en reliant ensemble leurs bornes homologues) ?
I-5) Calculer, pour le circuit de la fig. 2, la matrice $\left[ {\underline M } \right]$ définie par $\left[ {\begin{array}{*{20}{c}}{\underline {{V_2}} }\\{\underline {{I_2}} }\end{array}} \right] = \left[ {\underline M } \right]\left[ {\begin{array}{*{20}{c}}{\underline {{V_1}} }\\{\underline {{I_1}} }\end{array}} \right]$. Que devient cette relation lorsque $A$ tend vers l’infini ? Quelle relation existe-t-il alors entre les grandeurs réelles ${V_1}$ et ${V_2}$ d’une part, ${i_1}$ et ${i_2}$ d’autre part ?
I-7) On pose $K = \frac{{{R_1}}}{{{R_2}}}$. Donner l’expression des impédances $\underline {{Z_1}} $ et $\underline {{Z_2}} $ en fonction de $K$ dans les deux cas suivants : $\underline Z = R$ d’une part, $\underline Z = \frac{1}{{jC\omega }}$ d’autre part, impédance capacitive.
Deuxième partie : Réalisation d’un gyrateur
Un gyrateur est un quadripôle travaillant en régime linéaire sinusoïdal dont la matrice admittance s’écrit :$\left[ {\begin{array}{*{20}{c}}{\underline {{I_1}} }\\{\underline {{I_2}} }\end{array}} \right] = \left[ {\begin{array}{*{20}{c}}0&{ - \frac{Y}{a}}\\{aY}&0\end{array}} \right]\,\left[ {\begin{array}{*{20}{c}}{\underline {{V_1}} }\\{\underline {{V_2}} }\end{array}} \right]$. Les courants sont comptés positivement lorsqu’ils entrent dans le quadripôle, $Y$ est une admittance réelle positive et $a$ est un réel positif.
II-1) Quel est le rapport entre la puissance moyenne sortante et la puissance moyenne entrante ?
II-2) En déduire qu’un gyrateur fermé sur un composant qui ne consomme pas de puissance simule à l’entrée un composant qui ne consomme pas non plus de puissance.
II-3) Que peut-on dire du quadripôle si $a$ est strictement plus grand que l’unité ?
II-4) Exprimer$\underline {{Z_1}} $ , impédance d’entrée du gyrateur, en fonction de$\underline {{Z_u}} $ impédance placée en sortie. Préciser ces expressions lorsque le quadripôle est fermé sur une inductance $L$, ou sur une capacité $C$. C’est plutôt sous cette dernière forme que le gyrateur est généralement utilisé. Quelle en est, selon vous, la raison ?
II-6) Représenter par ses éléments un quadripôle dont la matrice admittance est : $\left[ {\begin{array}{*{20}{c}}{\frac{1}{{{R_1}}}}&0\\0&0\end{array}} \right]$.
II-7) Représenter par ses éléments un quadripôle dont la matrice admittance est : $\left[ {\begin{array}{*{20}{c}}{ - \frac{1}{{{R_1}}}}&0\\0&0\end{array}} \right]$. On utilisera à cet effet un amplificateur opérationnel, deux résistors de même résistance$R$ et un résistor de résistance ${R_1}$.
II-8) Comment brancher le quadripôle déterminé à la question II-7) sur celui de la fig. 4 pour obtenir un gyrateur ?
II-9) Avec le moins de calculs possibles, montrer que le schéma de la fig. 5 réalise un gyrateur et, toujours dans le cadre d’un régime de fonctionnement linéaire, donner les valeurs de $Y$ et de $a$ qui lui sont associées.
Troisième partie : Utilisation du gyrateur
III-1) La fig. 6 représente le gyrateur G de la fig. 5 fermé sur l’association de $R$ et ${C_2}$ montés en parallèle . Déterminer l’expression de la transmittance $\frac{\underline{{{V}_{s}}}}{\underline{{{V}_{e}}}}$du filtre ainsi réalisé (on pourra poser $\omega _0^2 = \frac{1}{{R_1^2{C_1}{C_2}}}$ et $Q = R{C_2}{\omega _0}$). Qu’a-t-on ainsi simulé ?
III-2) Quel est le rôle de l’amplificateur opérationnel en fin de montage ?
III-3) Donner l’expression de la fréquence d’accord, de la largeur de bande passante et du facteur de qualité de ce filtre, en fonction de la valeur de ses composants. Montrer que les réglages de la bande passante et de la fréquence d’accord sont indépendants l’un de l’autre.
FIN DE CE PROBLÈME
Première partie : Superposition d’écoulements
On considère l’écoulement d’un fluide incompressible parfait défini par le champ de vitesse ${\vec V_1} = \frac{\lambda }{{2\pi {r_1}}}{\vec u_1}$, où $\lambda $ est une constante réelle et ${r_1},\;{\theta _1}$ et $z$ les coordonnées cylindriques d’un point M par rapport au point A1 de coordonnées $\left( { - a,\;0,\;0} \right)$ dans un repère galiléen $\left( {O,\;x,\;y,\;z} \right)$ muni de la base orthonormée $\left( {\vec x,\;\vec y,\;\vec z} \right)$. Le point $H$ (fig. 1) étant la projection du point M sur le plan $\left( {xOy} \right)$, on a : $\vec{A_{1}M}= {r_1}{\vec u_1} + z\vec z$, où ${\vec u_1}$est le vecteur unitaire porté par $vec{A_{1}H}$.
I-1) Montrer que la circulation du vecteur ${\vec V_1}$ entre deux points A et B est indépendante du chemin suivi et déterminer le potentiel $\varphi {'_1}\left( {{r_1}} \right)$ associé à cet écoulement $\left( {{{\vec V}_1} = + {\bf{grad}}\left( {\varphi _1^{'}} \right)} \right)$, sachant qu’il est par convention nul pour une certaine valeur ${r_0}$ de ${r_1}$.
I-2) Cet écoulement suit-il la loi de Laplace $\Delta \varphi _1^{'} = 0$?
I-3) On superpose à l’écoulement précédent le nouvel écoulement défini par le champ de vitesse ${\vec V_2} = \frac{{ - \lambda }}{{2\pi {r_2}}}{\vec u_2}$, avec $\vec{A_{2}M}= \vec{A_{2}H}+ \vec{HM}={r_2}{\vec u_2} + z\vec z$ (fig. 2), les coordonnées du point A2 étant $\left( {a,\;0,\;0} \right)$. Quelle est l’expression du potentiel des vitesses ${\varphi _1}\left( {{r_1},\;{r_2}} \right)$ associé à l’écoulement résultant, l’origine des potentiels étant prise dans le plan $\left( {yOz} \right)$ ?
I-4) On fait tendre $a$ vers 0 et $\lambda $ vers l’infini, de telle sorte que le produit $2\lambda a=M$soit constant. Montrer que le potentiel en coordonnées cylindriques (vecteurs unitaires ${\vec u_r}$ et ${\vec u_\theta }$) s’écrit alors ${{\varphi }_{1}}=\frac{M\cos \theta }{2\pi r}$, où $\theta $ est l’angle entre $Ox$ et $OH$ (voir fig. 2).
I-5) Déterminer l’équation des lignes de courant ; tracer rapidement leur allure.
I-6) On superpose à cet écoulement un écoulement uniforme, de vitesse $\vec u = u\vec x$. Montrer qu’il existe pour l’écoulement résultant une ligne de courant circulaire d’axe $Oz$, dont on précisera le rayon $R$ en fonction de $M$ et de $u$. Donner alors, qualitativement, la forme des lignes de courant ; on distinguera les cas $r$<$R$ et $r$>$R$.
I-8) On superpose enfin un dernier écoulement, défini par la vitesse ${\vec V_3}$ pour $r$>$R$: ${\vec V_3} = \frac{C}{{2\pi r}}{\vec u_\theta }$, où $C$ est une constante. Montrer que cet écoulement dérive d’un potentiel ${\varphi _3}$, dont on ne demande pas d’établir l’expression. Quelle est la circulation du vecteur ${\vec V_3}$ sur une courbe fermée dans les deux cas où l’origine est à l’intérieur ou à l’extérieur de la courbe ? Voyez-vous une analogie, magnétostatique ou électrostatique, à ce problème d’écoulement ?
Deuxième partie : Voile de Flettner
Un bateau est muni d’un cylindre vertical de rayon $R$ et de hauteur $h$, tournant autour d’un axe vertical à la vitesse angulaire $\vec \omega = \omega \vec z$. Le vent souffle avec une vitesse uniforme constante $\vec u = u\vec x$. L’écoulement de potentiel des vitesses ${\varphi _t}$ de la question I-7) correspond à l’écoulement du vent autour du cylindre de rayon $R$, satisfaisant aux conditions aux limites. L’écoulement de potentiel des vitesses ${\varphi _3}$ de la question I-8) correspond à l’effet d’entraînement de l’air (de masse volumique $\rho $) par la rotation du cylindre.
II-1) Donner la relation entre la constante $C$ et $\omega $. On remarquera que, dans ce modèle, la vitesse du vent sur le cylindre est celle du cylindre, autrement dit que la vitesse tangentielle ne s’annule pas sur la paroi du cylindre (ce point relève, en fait, de la viscosité) .
II-2) Calculer, en coordonnées polaires, les composantes de la vitesse résultante pour $r$>$R$.
II-3) Sachant que, loin du bateau, le vent n’est pas perturbé et que la pression est égale à la pression atmosphérique normale ${p_c}$, déterminer, en fonction de l’angle $\theta $, la pression autour du cylindre ($r$=$R$).
II-4) Quelle est, en fonction de $R$, $C$, $\vec u$, $\vec z$ et de la masse volumique de l’air $\rho $, la résultante des forces de pression par unité de hauteur sur le cylindre ? On pourra aussi bien exprimer le résultat en fonction de $R$, $\rho $, $\vec u$ et $\vec \omega $.
II-5) Préciser sur un schéma le sens de rotation du cylindre correspondant à une force propulsive. Quelle est l’allure du vent la plus favorable (vent de près, vent de travers et vent arrière sont précisés sur la figure 3-a).
Troisième partie : Comparaison avec une voile classique
III-1) Une voile plane d’aire $\Sigma $ et de vecteur unitaire normal $\vec \sigma $ reçoit une veine de vent de vitesse $\vec u$ sous l’angle $\alpha $ et la réfléchit selon la loi de Descartes (fig. 3-b). Quel est le vecteur force exercé par le vent sur la voile ? On pourra introduire le débit $D = \rho \Sigma u\sin \alpha $.
III-2) Le bateau reçoit le vent par le travers (fig. 3-c), l’axe du bateau est perpendiculaire au vent relatif. Quelle est dans ces conditions, en fonction de $\rho $, $u$, $\Sigma $ et $\alpha $ la composante propulsive de la force précédente ?
III-3) Pour quelle valeur de $\alpha $ cette composante est-elle maximale ? De quel type de vent s’agit-il ? Calculer numériquement la force propulsive maximale avec le même vent qu’en II-6) ($u = 10\,{\rm{m}}{\rm{.}}{{\rm{s}}^{ - {\rm{1}}}},\;\rho = 1,3\,{\rm{kg}}{\rm{.}}{{\rm{m}}^{ - {\rm{3}}}}$) pour une voile de $25$m2. Comparer avec le cylindre de Flettner (le maximum de la fonction $\left( {{{\sin }^2}\alpha } \right)\cos \alpha $ vaut $0,385$).
FIN DE CE PROBLÈME
Aucun commentaire:
Enregistrer un commentaire