ULM M’ 95
1.1°) ${A_3} = \rho {A_1} + \tau '{A_2}$ et ${A_4} = \tau {A_1} + \rho '{A_2}$
${I_3} = {A_3}A_3^ * = {\left| \rho \right|^2}{\left| {{A_1}} \right|^2} + {\left| {\tau '} \right|^2}{\left| {{A_2}} \right|^2} + \rho \tau {'^ * }{A_1}A_2^ * + {\rho ^ * }\tau 'A_1^ * {A_2}$
${I_4} = {A_4}A_4^ * = {\left| \tau \right|^2}{\left| {{A_1}} \right|^2} + {\left| {\rho '} \right|^2}{\left| {{A_2}} \right|^2} + \rho {'^ * }\tau \;{A_1}A_2^ * + \rho '{\tau ^ * }A_1^ * {A_2}$
1.2°) Conservation de l’énergie: ${I_3} + {I_4} = {I_1} + {I_2} = ({\left| \rho \right|^2} + {\left| \tau \right|^2}){I_1} + ({\left| {\rho '} \right|^2} + {\left| {\tau '} \right|^2}){I_2} + (\rho \tau {'^*} + \tau \rho {'^*}){A_1}A_2^ * + ({\rho ^ * }\tau ' + {\tau ^ * }\rho ')A_1^ * {A_2}$
${A_2} = 0$$ \Rightarrow $${\left| \rho \right|^2} + {\left| \tau \right|^2} = 1$ et ${A_1} = 0$$ \Rightarrow $${\left| {\rho '} \right|^2} + {\left| {\tau '} \right|^2} = 1$
Il reste $(\rho \tau {'^ * } + \tau \rho {'^ * }){A_1}A_2^ * + ({\rho ^ * }\tau ' + {\tau ^ * }\rho ')A_1^ * {A_2} = 0$ soit ${\mathop{\rm Re}\nolimits} \{ (\rho \tau {'^ * } + \tau \rho {'^ * }){A_1}A_2^ * \} = 0$, valable $\forall $ l’argument de ${A_1}A_2^ * $ d’où $\rho \tau {'^ * } + \tau \rho {'^ * } = 0$
1.3°.α) $\rho = \rho ' = ir$ et $\tau = \tau ' = t$ $ \Rightarrow $${r^2} + {t^2} = 1$ et $irt - irt = 0$
1.3°.β) $\rho = - \rho ' = r$ et $\tau = \tau ' = t$ $ \Rightarrow $${r^2} + {t^2} = 1$ et $rt - rt = 0$
Pour décider de l’un ou l’autre cas, il faut imaginer que la réflexion se fait sur un plan de référence (π) et que le déphasage est du à un parcours dans l’épaisseur d’un dépôt métallique. En plus le plan de référence peut produire un déphasage de 0 ou π mais il est le même que le rayon arrive à gauche ou à droite.
Dans le cas α, le plan de référence est au milieu d’une couche métallique; un déphasage de $\frac{\pi }{2}$ se fait selon le trajet AIB pour le rayon de gauche et selon CID pour le rayon de droite.
Dans le cas β, le plan de référence est confondu avec une des faces de la lame métallique; un déphasage de $\pi $ se fait selon IAB pour le rayon de gauche et aucun déphasage pour le rayon de droite.
Dans le Fabry-Pérot (dépôt métallique sur verre), c’est le cas réalisé.
2.1°) On prend $\rho = - \rho ' = r$ et $\tau = \tau ' = t$ et on pose $\varphi = \frac{{4\pi d}}{\lambda } = \frac{{4\pi \nu d}}{c}$
Les lames sont supposées symétriques l’une de l’autre par rapport au plan médian.
Les amplitudes indiquées dans la lame sont les valeurs à droite pour l’onde se propageant vers la droite et les valeurs à gauche pour l’onde se propageant vers la gauche (sans indication des facteurs exponentiels).
$\frac{{{A_1}}}{{{A_0}}} = \tau \tau '{e^{ - j\frac{\varphi }{2}}}\sum\limits_{q = 0}^\infty {\rho {'^{2q}}{e^{ - jq\varphi }}} $ $ \Rightarrow $ $\frac{{{A_1}}}{{{A_0}}} = \frac{{{t^2}{e^{ - j\frac{\varphi }{2}}}}}{{1 - {r^2}{e^{ - j\varphi }}}}$
$\frac{{{I_1}}}{{{I_0}}} = \frac{{{{(1 - {r^2})}^2}}}{{1 + {r^4} - 2{r^2}\cos \varphi }}$
$\frac{{{I_1}}}{{{I_0}}} = \frac{1}{{1 + m{{\sin }^2}\frac{\varphi }{2}}}$ avec $m = \frac{{4{r^2}}}{{{{(1 - {r^2})}^2}}}$ soit $m = \frac{4}{{{\varepsilon ^2}}}$
$\frac{{{A_2}}}{{{A_0}}} = \rho + \tau \tau '\rho {e^{ - j\varphi }}\sum\limits_{q = 0}^\infty {\rho {'^{2q}}{e^{ - jq\varphi }}} $$ = \rho (1 - \frac{{{t^2}{e^{ - j\varphi }}}}{{1 - {r^2}{e^{ - j\varphi }}}})$$ = \rho \frac{{1 - {e^{ - j\varphi }}}}{{1 - {r^2}{e^{ - j\varphi }}}}$
$\frac{{{I_2}}}{{{I_0}}} = \frac{{m{{\sin }^2}\frac{\varphi }{2}}}{{1 + m{{\sin }^2}\frac{\varphi }{2}}}$ avec $m = \frac{4}{{{\varepsilon ^2}}}$; on bien ${I_1} + {I_2} = {I_0}$ (ainsi, on aurait pu avoir ${I_2}$ à partir de ${I_1}$); la période en $\varphi = \frac{{4\pi \nu d}}{c}$ est égale à $2\pi $ $ \Rightarrow $ ${I_1}$ et ${I_2}$ sont périodiques en fréquence de périodicité $\Delta \nu = \frac{c}{{2d}}$
2.2°) $\varepsilon < < 1 \Rightarrow m = \frac{4}{{{\varepsilon ^2}}} > > 1$.
On a un maximum de ${I_1}$ égal à ${I_0}$ si $\varphi = 2q\pi $ soit si $d = q\frac{c}{{2\nu }}$ et un minimum égal à $\frac{{{I_0}}}{{1 + m}}$ voisin de 0 si $\varphi = (2q + 1)\pi $ soit si $d = (q + \frac{1}{2})\frac{c}{{2\nu }}$; la courbe représentative est donnée ci-contre.
Soit $2\xi $ la largeur à mi-hauteur d’un pic avec $\xi $tel que $d = q\frac{c}{{2\nu }} \pm \xi $ $ \Rightarrow $ $\varphi = 2\pi q \pm \frac{{4\pi \nu \xi }}{c}$ et ${I_1} = \frac{{{I_0}}}{2}$ $ \Rightarrow $ $m{\sin ^2}(\pi q \pm \frac{{2\pi \nu \xi }}{c}) = 1$ $ \Rightarrow $ $\sin (\frac{{2\pi \nu \xi }}{c}) = \pm \frac{1}{{\sqrt m }}$ et donc $2\xi = \frac{c}{{\pi \nu \sqrt m }} < < \frac{c}{{2\nu }}$ $ \Rightarrow $ les pics sont très étroits.
2.3°) Entre deux pics successifs $\Delta d = \frac{c}{{2\nu }} = \frac{\lambda }{2}$ (la moitié de la longueur d’onde).
2.4°) Si $\nu \to \nu + d\nu $, les abscisses des pics associés à $\nu $ sont ${d_q} = q\frac{c}{{2\nu }}$ et celles des pics associés à $\nu + d\nu $ sont $d{'_q} = q\frac{c}{{2(\nu + d\nu )}}$; on obtient une série de doubles pics.
2.5°) A la limite de séparation le bord droit, à mi-hauteur, d’un pic, coïncide avec le bord gauche, à mi-hauteur de l’autre pic.
La courbe ci-contre représente les deux pics dans cette position et la courbe résultante.
On aura séparation si $d{'_q} - {d_q} > 2\xi $ soit si $q\frac{c}{2}(\frac{1}{\nu } - \frac{1}{{\nu + d\nu }}) > 2\xi = \frac{2}{{\pi \nu \sqrt m }}$ $ \Rightarrow $ $\delta \nu > \frac{{2\nu }}{{q\pi \sqrt m }}$
Mais $d = \frac{{qc}}{{2\nu }}$ $ \Rightarrow $ $\delta \nu = \frac{c}{{d\pi \sqrt m }}$ ou $\delta {\nu _m} = \frac{{\varepsilon c}}{{2\pi d}}$
2.6°) $\varepsilon = {10^{ - 3}}\;et\;m = {4.10^6}$ $ \Rightarrow $ $\delta {\nu _m} = {10^6}Hz$
$d = q\frac{c}{{2\nu }}$ $ \Rightarrow $ $\Delta d = - d\frac{{\Delta \nu }}{\nu }$ or $\nu = \frac{c}{\lambda } = {4.74.10^{14}}Hz$
soit $\Delta d = - {10^{ - 10}}m$
2.7°) Le double pic peut être dû au voisinage d’un pic d’ordre q pour la radiation de longueur d’onde $\lambda $et d’un pic d’ordre q+p pour la radiation de longueur d’onde $\lambda + d\lambda $: ${d_\lambda } = q\frac{\lambda }{2}$ et ${d_{\lambda + d\lambda }} = (q + p)\frac{{\lambda + d\lambda }}{2}$; on a confusion des deux pics si ${d_\lambda } = {d_{\lambda + d\lambda }}$ $ \Rightarrow \;d = - p\frac{{{\lambda ^2}}}{{2\Delta \lambda }}$ avec $p = \pm 1, \pm 2,...$; pour $\Delta \nu $ de l’ordre de $\Delta {\nu _m}$, $d = - p\frac{c}{{\Delta {\nu _m}}} = - 300p$ soit 300 m pour $p = \pm 1$; or d=5cm; pour des raies de structure hyperfine:
on peut conclure avec certitude.
2.8°) ${I_{1\;\max }} = {I_0}$
2.9°) ${I_1} + {I_2} = {I_0}$
2.10°) $\frac{{{A_ - }}}{{{A_0}}} = \rho '\tau {e^{ - j\frac{\varphi }{2}}}\sum\limits_{q = 0}^\infty {\rho {'^{2q}}{e^{ - jq\varphi }}} $=$\frac{{\rho '\tau {e^{ - j\frac{\varphi }{2}}}}}{{1 - \rho {'^2}{e^{ - j\varphi }}}}$ $ \Rightarrow $ $\frac{{{I_ - }}}{{{I_0}}} = \frac{{1 - \varepsilon }}{\varepsilon }\frac{1}{{1 + m{{\sin }^2}\frac{\varphi }{2}}}$
$\frac{{{A_ - }}}{{{A_0}}} = \tau \sum\limits_{q = 0}^\infty {\rho {'^{2q}}{e^{ - jq\varphi }}} $=$\frac{\tau }{{1 - \rho {'^2}{e^{ - j\varphi }}}}$ $ \Rightarrow $ $\frac{{{I_ - }}}{{{I_0}}} = \frac{1}{\varepsilon }\;\frac{1}{{1 + m{{\sin }^2}\frac{\varphi }{2}}}$
$\varepsilon < < 1$ ${I_ - } \approx {I_ + } \approx \;\frac{1}{\varepsilon }\;\frac{1}{{1 + m{{\sin }^2}\frac{\varphi }{2}}}$ avec $m = \frac{4}{{{\varepsilon ^2}}}$; il y a résonance pour $I = {I_0}$.
2.11°) A travers une surface S parallèle aux miroirs, entre eux, le flux du vecteur de Poynting est $\vec \pi .\vec S = ({\vec \pi _ + } - {\vec \pi _ - }).\vec S$ et représente le différence entre le flux d’énergie dû à l’onde + et celui dû à l’onde -.
2.12°) Avec n entier relatif: $\varphi = 2\pi n + \frac{{4\pi d}}{c}(\nu - {\nu _n})$; à mi-hauteur $\sin 2\pi \frac{d}{c}(\nu - {\nu _n}) = \pm \frac{1}{{\sqrt m }}$ d’où $\delta \nu = \frac{c}{{d\pi \sqrt m }}$ et $\frac{{{I_1}}}{{{I_0}}} = \frac{1}{{1 + 4{{\left( {\frac{{\nu - {\nu _m}}}{{\Delta \nu }}} \right)}^2}}}$.
Le facteur 4 a été oublié dans le texte qui précisait bien largeur à mi-hauteur et non demi-largeur à mi-hauteur.
$Q = \frac{{{\nu _n}}}{{\Delta \nu }} = \frac{{d\pi \sqrt m \nu }}{c} = \frac{{2d\pi \nu }}{{\varepsilon c}} = \frac{{2d\pi }}{{\varepsilon \lambda }}$ $Q = {5.10^8}$
2.13°) On tient compte des durées de propagation; on étudie le régime transitoire du Fabry-Pérot; on prend la date t=0 quand le premier rayon transmis sort de l’appareil.
$\frac{{{A_1}}}{{{A_0}}} = {t^2}\sum\limits_{l = 0}^n {{r^{2l}}} {e^{ - jl\varphi }}$ avec $\varphi = 2q\pi $ (résonance) soit $\frac{{{A_1}}}{{{A_0}}} = {t^2}\sum\limits_{l = 0}^n {{r^{2l}}} $$ = 1 - {r^{2(n + 1)}}$ et $\frac{{{I_1}}}{{{I_0}}} = {\left[ {1 - {r^{2(n + 1)}}} \right]^2}$ avec $n = \frac{{ct}}{{2d}}$; ${I_1}$ tend vers zéro quand n tend vers l’infini; on se ramène à $\frac{{{I_1}}}{{{I_0}}} = {\left[ {1 - {r^{\frac{{ct}}{d}}}} \right]^2}$ après un décalage des temps légitime de 2d/c quand on passe d’une fonction discontinue en escalier à une fonction continue.
$\frac{{{A_1}}}{{{A_0}}} = {t^2}\sum\limits_{l = 0}^n {{r^{2l}}} {e^{ - jl\varphi }}$$ = {r^{2n + 1}}$ et $\frac{{{I_2}}}{{{I_0}}} = {r^{2(2n + 1)}}$; ${I_2}$ tend vers zéro quand n tend vers l’infini.
2.14°) ${r^2} = 1 - \varepsilon \approx {e^{ - \varepsilon }}$ $ \Rightarrow \;{I_1}(t) = {I_0}{\left( {1 - {e^{ - \frac{{\varepsilon ct}}{{2d}}}}} \right)^2}$; on ne trouve pas la formule du texte dans lequel l’exposant 2 a vraisemblablement été oublié.
2.15°) ${\tau _c} = \frac{{2d}}{{c\varepsilon }}$
2.16°) ${\tau _c}\Delta \nu = \frac{1}{\pi }$ (on trouve ${\tau _c}\Delta \nu = \frac{1}{{2\pi }}$ en prenant la demi-largeur à demi-hauteur).
2.17°) A l’instant initial, l’onde arrête d’émerger du Fabry-Pérot; la série géométrique est tronquée au début alors que c’était à la fin en 2.13°; $\frac{{{A_1}}}{{{A_0}}} = {\left( {\frac{{{A_1}}}{{{A_0}}}} \right)_{n \to \infty (2.13^\circ )}} - {\left( {\frac{{{A_1}}}{{{A_0}}}} \right)_{(2.13^\circ )}} = {r^{2(n + 1)}}$d’où $\frac{{{I_1}}}{{{I_0}}} = {r^{4(n + 1)}}$ et $\frac{{{I_1}}}{{{I_0}}} = {e^{ - \frac{{\varepsilon ct}}{d}}}$
et de même: $\frac{{{A_2}}}{{{A_0}}} = {\left( {\frac{{{A_2}}}{{{A_0}}}} \right)_{n \to \infty (2.13^\circ )}} - {\left( {\frac{{{A_2}}}{{{A_0}}}} \right)_{(2.13^\circ )}} = - {r^{2n + 1}}$d’où $\frac{{{I_2}}}{{{I_0}}} = {r^{2(2n + 1)}}$ et $\frac{{{I_2}}}{{{I_0}}} = {e^{ - \frac{{\varepsilon ct}}{d}}}$
2.18°) Pour les deux intensités, la limite, quand n tend vers l’infini, est nulle alors qu’en 2.13° elle est ${I_0}$ et 0 respectivement.
2.19°) L’onde n’est pas résonnante: si $n \to \infty $, pour l’établissement: $\frac{{{I_1}}}{{{I_0}}} \to \frac{1}{{1 + m{{\sin }^2}\frac{\varphi }{2}}}$ et $\frac{{{I_2}}}{{{I_0}}} \to \frac{{m{{\sin }^2}\frac{\varphi }{2}}}{{1 + m{{\sin }^2}\frac{\varphi }{2}}}$ alors que pour la rupture, les deux intensités tendent vers zéro.
2.20°) On indique « lentement » car il faut qu’un régime quasi-stationnaire soit réalisé et donc que la durée de déplacement soit très supérieure au temps de stockage de la cavité.
3.1°) On considère 2 miroirs identiques (pas dit dans le texte): $A\xrightarrow[{{M}_{1}}]{}{{A}_{1}}\xrightarrow[{{M}_{2}}]{}{{A}_{2}}\xrightarrow[{{M}_{1}}]{}{{A}_{3}}\xrightarrow[{{M}_{2}}]{}{{A}_{4}}$
${\overline {FA} _1}.\overline {FA} = {\overline {FA} _1}.{\overline {FA} _2}$ (formule de conjugaison de Newton) implique qu’après deux réflexions l’image A2 se confond avec l’objet A; le grandissement transversal, selon les formules de Newton, après ces deux réflexions est ${\gamma _t} = \frac{{ - {f_2}}}{{\overline {F{A_1}} }}.\frac{{ - \overline {F{A_1}} }}{{{f_1}}} = - 1$ et l’image d’un petit objet rectiligne perpendiculaire à l’axe est renversée; après 4 réflexions, deux sur chaque miroir, l’image d’un petit objet rectiligne perpendiculaire à l’axe se confond avec l’objet. D’après la relation de Lagrange-Helmoltz $G{\gamma _t} = - 1$ pour un miroir et +1 pour un nombre pair de miroirs; on a donc le grandissement angulaire G=1.
Après 4 réflexions le rayon repart du même point de l’axe dans les mêmes direction et sens.
3.2°) L = 2f = R (rayon des miroirs)
Soit A le point sur l’axe de révolution; tout rayon issu de A repasse en A après 4 réflexions, dans le cadre de l’approximation de Gauss, d’où: $(A{A_4}) = 4L = 8f = 4R$; le chemin optique ne dépend pas du rayon considéré (stigmatisme approché); il ne dépend pas de l’angle d’inclinaison; en posant $\varphi = \frac{{8\pi \nu R}}{c}$, on a le tableau suivant des amplitudes internes (juste avant sortie de la cavité):
où ${\varphi _0},{\varphi _1},{\varphi _2},\varphi $ sont les déphasages le long des trajets internes.
$\frac{{{A_1}}}{{{A_0}}} = \tau \tau '{e^{ - j{\varphi _0}}}\sum\limits_{q = 0}^\infty \rho {'^{4q}}{e^{ - jq\varphi }} = \frac{{{t^2}{e^{ - j{\varphi _0}}}}}{{1 - {r^4}{e^{ - j\varphi }}}}$ $ \Rightarrow $ $\frac{{{I_1}}}{{{I_0}}} = \frac{{{{(1 - {r^2})}^2}}}{{{{(1 - {r^4})}^2} + 4{r^4}{{\sin }^2}\frac{\varphi }{2}}}$
$\frac{{{A_2}}}{{{A_0}}} = \tau \tau '\rho '{e^{ - j{\varphi _1}}}\sum\limits_{q = 0}^\infty \rho {'^{4q}}{e^{ - jq\varphi }} = \frac{{ - r{t^2}{e^{ - j{\varphi _1}}}}}{{1 - {r^4}{e^{ - j\varphi }}}}$ $ \Rightarrow $ $\frac{{{I_2}}}{{{I_0}}} = \frac{{{r^2}{{(1 - {r^2})}^2}}}{{{{(1 - {r^4})}^2} + 4{r^4}{{\sin }^2}\frac{\varphi }{2}}}$
$\frac{{{A_3}}}{{{A_0}}} = \tau \tau '\rho {'^2}{e^{ - j{\varphi _2}}}\sum\limits_{q = 0}^\infty \rho {'^{4q}}{e^{ - jq\varphi }} = \frac{{{r^2}{t^2}{e^{ - j{\varphi _2}}}}}{{1 - {r^4}{e^{ - j\varphi }}}}$ $ \Rightarrow $ $\frac{{{I_3}}}{{{I_0}}} = \frac{{{r^4}{{(1 - {r^2})}^2}}}{{{{(1 - {r^4})}^2} + 4{r^4}{{\sin }^2}\frac{\varphi }{2}}}$
$\frac{{{A_4}}}{{{A_0}}} = \rho + \tau \tau '\rho {'^3}{e^{ - j\varphi }}\sum\limits_{q = 0}^\infty \rho {'^{4q}}{e^{ - jq\varphi }} = \frac{{r(1 - {r^2}{e^{ - j\varphi }})}}{{1 - {r^4}{e^{ - j\varphi }}}}$ $ \Rightarrow $ $\frac{{{I_4}}}{{{I_0}}} = \frac{{{r^2}\left[ {{{(1 - {r^2})}^2} + 4{r^2}{{\sin }^2}\frac{\varphi }{2}} \right]}}{{{{(1 - {r^4})}^2} + 4{r^4}{{\sin }^2}\frac{\varphi }{2}}}$
On vérifie que la somme des quatre intensités est l’intensité incidente.
3.3°) Le trajet admet z’z comme axe de symétrie d’où ${\varphi _2} - {\varphi _0} = \frac{\varphi }{2}$ et $\frac{{{A_3}}}{{{A_1}}} = {r^2}{e^{ - j\frac{\varphi }{2}}}$; à la résonance $\varphi = 2q\pi $ $ \Rightarrow $
${A_1}\;et\;{A_3}$ sont en phase si q est pair et en opposition de phase si q est impair.
3.4°) Les rayons (1) et (3) sont confondus avec z’z; on se retrouve dans le cas d’un Fabry-Pérot plan-plan d’où $\frac{{{I_{13}}}}{{{I_0}}} = \frac{{{{(1 - {r^2})}^2}}}{{1 + {r^4} - 2{r^2}\cos \frac{\varphi }{2}}}$ ce qu’on retrouve mais par un calcul compliqué en faisant interférer les ondes (1) et (3).
4.1°) Du fait de la symétrie de révolution (xOz et yOz, plans de symétrie équivalents), on peut montrer facilement qu’entre grandeurs de sortie et grandeurs d’entrée, pour un rayon quelconque: $\left( {\begin{array}{*{20}{c}}{{x_{n + 1}}}\\{{\alpha _{n + 1}}}\\{{y_{n + 1}}}\\{{\beta _{n + 1}}}\end{array}} \right) = \left( {\begin{array}{*{20}{c}}a&b&0&0\\c&d&0&0\\0&0&a&b\\0&0&c&d\end{array}} \right)\left( {\begin{array}{*{20}{c}}{{x_n}}\\{{\alpha _n}}\\{{y_n}}\\{{\beta _n}}\end{array}} \right)$
Ceci revient à étudier la projection d’un rayon sur les plans xOz et yOz; il suffit d’étudier la marche d’un rayon méridien.
4.2°) On obtient quatre relations:
a) Dans le vide de gauche à droite: $y{'_n} = {y_n} + {\alpha _n}L$
b) Réflexion sur M2 , à droite: avec la relation de conjugaison (origine au sommet): $\alpha {'_n} = - {\alpha _n} - \frac{{2y{'_n}}}{{\overline {{S_2}{C_2}} }}$
c) Dans le vide de droite à gauche: ${y_{n + 1}} = {y_n} - \alpha {'_n}L$
d) Réflexion sur le miroir de gauche M1: ${\alpha _{n + 1}} = - \alpha {'_n} - \frac{{2{y_{n + 1}}}}{{\overline {{S_1}{C_1}} }}$
D’où par éliminations successives, la relation matricielle: $\left( {\begin{array}{*{20}{c}}{{y_{n + 1}}}\\{{\alpha _{n + 1}}}\end{array}} \right) = \left( {\begin{array}{*{20}{c}}{1 + \frac{{2L}}{{\overline {{S_2}{C_2}} }}}&{2L(1 + \frac{L}{{\overline {{S_2}{C_2}} }})}\\{\frac{2}{{\overline {{S_2}{C_2}} }} - \frac{2}{{\overline {{S_1}{C_1}} }} - \frac{{4L}}{{\overline {{S_1}{C_1}\;} \overline {{S_2}{C_2}} }}}&{1 + \frac{{2L}}{{\overline {{S_2}{C_2}} }} - \frac{{4L}}{{\overline {{S_1}{C_1}} }}(1 + \frac{L}{{\overline {{S_2}{C_2}} }})}\end{array}} \right)\left( {\begin{array}{*{20}{c}}{{y_n}}\\{{\alpha _n}}\end{array}} \right)$
On remarque que le déterminant de la matrice de transfert vaut l’unité; on peut le voir par calcul direct ou bien en calculant la matrice comme produit de quatre matrices élémentaires chacune de déterminant unité.
4.3°) $\left( {\begin{array}{*{20}{c}}{{y_n}}\\{{\alpha _n}}\end{array}} \right) = {M^n}\left( {\begin{array}{*{20}{c}}{{y_0}}\\{{\alpha _0}}\end{array}} \right)$; dans la base des vecteurs propres de M, M et sa puissance n sont diagonales d’éléments diagonaux les valeurs propres: $({\lambda _1},{\lambda _2})$ et $(\lambda _1^n,\lambda _2^n)$; on en déduit que la solution dans la base des vecteurs propres est ${Y_n} = \lambda _1^n{Y_0}$ et ${A_n} = \lambda _2^n{A_0}$; à l’aide de la matrice de changement de base, on repasse dans la base initiale; ${y_n}$ et ${\alpha _n}$ sont donc combinaisons linéaires de $\lambda _1^n\;et\;\lambda _2^n$; les coefficients ne dépendent pas de n; l’équation aux valeurs propres, avec le déterminant de la matrice de transfert égal à l’unité est: ${\lambda ^2} - \lambda trace(M) + 1 = 0$; on en déduit que le produit des valeurs propres (complexes) vaut l’unité: ${\lambda _1}{\lambda _2} = 1$; les valeurs propres peuvent s’écrire sous la forme: ${\lambda _1} = \rho {e^{i\theta }}$ et ${\lambda _2} = \frac{1}{\rho }{e^{ - i\theta }}$; si $\rho \ne 1$ l’une des racines a un module supérieur à l’unité et donc ${y_n}$ et ${\alpha _n}$ divergent quand n devient grand: il y a instabilité. Pour avoir stabilité, il faut $\rho = 1$.
4.4°) Les deux valeurs propres sont imaginaires: ${\lambda _1} = {e^{i\theta }}$ et ${\lambda _2} = {e^{ - i\theta }}$; de ce fait: $trace(M) = a + d = 2\cos \theta $; la condition de stabilité est donc: $ - 2 \le a + d \le 2$ soit en remplaçant a et d par leurs valeurs et en posant ${g_i} = 1 - \frac{L}{{{R_i}}}$ le résultat: $0 \le {g_1}{g_2} \le 1$.
4.5°) Le domaine de stabilité est compris entre les deux branches de l’hyperbole équilatère.
Pour le Fabry-Pérot plan-plan les rayons de courbures sont infinis: le point (1,1) est le point représentatif.
Pour le Fabry-Pérot confocal les rayons sont égaux à L, le point représentatif est l’origine des axes.
4.6°) On veut ${y_n} = {y_0}$, ${x_n} = {x_0}$, ${\alpha _n} = {\alpha _0}$, ${\beta _n} = {\beta _0}$ $ \Rightarrow {M^n} = I$ (matrice unité); dans la base des vecteurs propres, cette propriété reste vraie d’où $\lambda _1^n = 1\;et\;\lambda _2^n = 1$ et du fait que le produit des valeurs propres vaut l’unité: ${\lambda _1} = {e^{\frac{{2\pi iq}}{n}}}$ et ${\lambda _1} = {e^{ - \frac{{2\pi iq}}{n}}}$; d’où ${\lambda _1} + {\lambda _2} = 2\cos \frac{{2\pi q}}{n} = a + d$; avec les rayons égaux $\cos \frac{{2\pi q}}{n} = 1 - \frac{{4L}}{R} + 2\frac{{{L^2}}}{{{R^2}}}$ ce qui conduit à l’équation ${\left( {\frac{L}{R}} \right)^2} - 2\left( {\frac{L}{R}} \right) + {\sin ^2}\frac{{\pi q}}{n} = 0$ de racines $\frac{L}{R} = 1 \pm \cos \frac{{q\pi }}{n}$ $q \in \left\{ {0..n - 1} \right\}$.
4.7°) ${x_k}\;et\;{y_k}$ sont combinaisons linéaires de $\lambda _1^k\;et\;\lambda _2^k$ avec des coefficients indépendants de k; on en déduit ${x_k} = A\cos (2\pi \frac{{kq}}{n} + {\varphi _x})$ et ${y_k} = A\cos (2\pi \frac{{kq}}{n} + {\varphi _y})$; il suffit que $qk \in \left\{ {0..n - 1} \right\}$ pour avoir toutes les valeurs possibles; on a bien n taches qui se répartissent sur une ellipse définie par son équation paramétrique.
4.8°) Si le trou est assez petit, le faisceau ne ressort plus quand L n’a pas exactement une des valeurs précédentes mais les taches en grand nombre, recouvrent une courbe proche de l’ellipse.
4.9°) Cavité multipassage: si n est élevé, le faisceau sera très affaibli (multiplication de l’intensité par ${r^{2n}}$); pour le Fabry-Pérot sphérique, à résonance, ${I_4} = \frac{{{I_0}}}{4}$; il est meilleur du point de vue de l’intensité émergente.
5.1°) $\Delta \vec E - \frac{1}{{{c^2}}}\frac{{{\partial ^2}\vec E}}{{\partial {t^2}}} = 0$ et $\Delta \vec B - \frac{1}{{{c^2}}}\frac{{{\partial ^2}\vec B}}{{\partial {t^2}}} = 0$1.1°) ${A_3} = \rho {A_1} + \tau '{A_2}$ et ${A_4} = \tau {A_1} + \rho '{A_2}$
${I_3} = {A_3}A_3^ * = {\left| \rho \right|^2}{\left| {{A_1}} \right|^2} + {\left| {\tau '} \right|^2}{\left| {{A_2}} \right|^2} + \rho \tau {'^ * }{A_1}A_2^ * + {\rho ^ * }\tau 'A_1^ * {A_2}$
${I_4} = {A_4}A_4^ * = {\left| \tau \right|^2}{\left| {{A_1}} \right|^2} + {\left| {\rho '} \right|^2}{\left| {{A_2}} \right|^2} + \rho {'^ * }\tau \;{A_1}A_2^ * + \rho '{\tau ^ * }A_1^ * {A_2}$
1.2°) Conservation de l’énergie: ${I_3} + {I_4} = {I_1} + {I_2} = ({\left| \rho \right|^2} + {\left| \tau \right|^2}){I_1} + ({\left| {\rho '} \right|^2} + {\left| {\tau '} \right|^2}){I_2} + (\rho \tau {'^*} + \tau \rho {'^*}){A_1}A_2^ * + ({\rho ^ * }\tau ' + {\tau ^ * }\rho ')A_1^ * {A_2}$
${A_2} = 0$$ \Rightarrow $${\left| \rho \right|^2} + {\left| \tau \right|^2} = 1$ et ${A_1} = 0$$ \Rightarrow $${\left| {\rho '} \right|^2} + {\left| {\tau '} \right|^2} = 1$
Il reste $(\rho \tau {'^ * } + \tau \rho {'^ * }){A_1}A_2^ * + ({\rho ^ * }\tau ' + {\tau ^ * }\rho ')A_1^ * {A_2} = 0$ soit ${\mathop{\rm Re}\nolimits} \{ (\rho \tau {'^ * } + \tau \rho {'^ * }){A_1}A_2^ * \} = 0$, valable $\forall $ l’argument de ${A_1}A_2^ * $ d’où $\rho \tau {'^ * } + \tau \rho {'^ * } = 0$
1.3°.β) $\rho = - \rho ' = r$ et $\tau = \tau ' = t$ $ \Rightarrow $${r^2} + {t^2} = 1$ et $rt - rt = 0$
Pour décider de l’un ou l’autre cas, il faut imaginer que la réflexion se fait sur un plan de référence (π) et que le déphasage est du à un parcours dans l’épaisseur d’un dépôt métallique. En plus le plan de référence peut produire un déphasage de 0 ou π mais il est le même que le rayon arrive à gauche ou à droite.
Dans le cas α, le plan de référence est au milieu d’une couche métallique; un déphasage de $\frac{\pi }{2}$ se fait selon le trajet AIB pour le rayon de gauche et selon CID pour le rayon de droite.
Dans le cas β, le plan de référence est confondu avec une des faces de la lame métallique; un déphasage de $\pi $ se fait selon IAB pour le rayon de gauche et aucun déphasage pour le rayon de droite.
Dans le Fabry-Pérot (dépôt métallique sur verre), c’est le cas réalisé.
2.1°) On prend $\rho = - \rho ' = r$ et $\tau = \tau ' = t$ et on pose $\varphi = \frac{{4\pi d}}{\lambda } = \frac{{4\pi \nu d}}{c}$
Les lames sont supposées symétriques l’une de l’autre par rapport au plan médian.
Les amplitudes indiquées dans la lame sont les valeurs à droite pour l’onde se propageant vers la droite et les valeurs à gauche pour l’onde se propageant vers la gauche (sans indication des facteurs exponentiels).
$\frac{{{A_1}}}{{{A_0}}} = \tau \tau '{e^{ - j\frac{\varphi }{2}}}\sum\limits_{q = 0}^\infty {\rho {'^{2q}}{e^{ - jq\varphi }}} $ $ \Rightarrow $ $\frac{{{A_1}}}{{{A_0}}} = \frac{{{t^2}{e^{ - j\frac{\varphi }{2}}}}}{{1 - {r^2}{e^{ - j\varphi }}}}$
$\frac{{{I_1}}}{{{I_0}}} = \frac{{{{(1 - {r^2})}^2}}}{{1 + {r^4} - 2{r^2}\cos \varphi }}$
$\frac{{{I_1}}}{{{I_0}}} = \frac{1}{{1 + m{{\sin }^2}\frac{\varphi }{2}}}$ avec $m = \frac{{4{r^2}}}{{{{(1 - {r^2})}^2}}}$ soit $m = \frac{4}{{{\varepsilon ^2}}}$
$\frac{{{A_2}}}{{{A_0}}} = \rho + \tau \tau '\rho {e^{ - j\varphi }}\sum\limits_{q = 0}^\infty {\rho {'^{2q}}{e^{ - jq\varphi }}} $$ = \rho (1 - \frac{{{t^2}{e^{ - j\varphi }}}}{{1 - {r^2}{e^{ - j\varphi }}}})$$ = \rho \frac{{1 - {e^{ - j\varphi }}}}{{1 - {r^2}{e^{ - j\varphi }}}}$
$\frac{{{I_2}}}{{{I_0}}} = \frac{{m{{\sin }^2}\frac{\varphi }{2}}}{{1 + m{{\sin }^2}\frac{\varphi }{2}}}$ avec $m = \frac{4}{{{\varepsilon ^2}}}$; on bien ${I_1} + {I_2} = {I_0}$ (ainsi, on aurait pu avoir ${I_2}$ à partir de ${I_1}$); la période en $\varphi = \frac{{4\pi \nu d}}{c}$ est égale à $2\pi $ $ \Rightarrow $ ${I_1}$ et ${I_2}$ sont périodiques en fréquence de périodicité $\Delta \nu = \frac{c}{{2d}}$
2.2°) $\varepsilon < < 1 \Rightarrow m = \frac{4}{{{\varepsilon ^2}}} > > 1$.
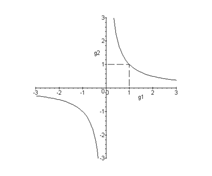
On a un maximum de ${I_1}$ égal à ${I_0}$ si $\varphi = 2q\pi $ soit si $d = q\frac{c}{{2\nu }}$ et un minimum égal à $\frac{{{I_0}}}{{1 + m}}$ voisin de 0 si $\varphi = (2q + 1)\pi $ soit si $d = (q + \frac{1}{2})\frac{c}{{2\nu }}$; la courbe représentative est donnée ci-contre.
Soit $2\xi $ la largeur à mi-hauteur d’un pic avec $\xi $tel que $d = q\frac{c}{{2\nu }} \pm \xi $ $ \Rightarrow $ $\varphi = 2\pi q \pm \frac{{4\pi \nu \xi }}{c}$ et ${I_1} = \frac{{{I_0}}}{2}$ $ \Rightarrow $ $m{\sin ^2}(\pi q \pm \frac{{2\pi \nu \xi }}{c}) = 1$ $ \Rightarrow $ $\sin (\frac{{2\pi \nu \xi }}{c}) = \pm \frac{1}{{\sqrt m }}$ et donc $2\xi = \frac{c}{{\pi \nu \sqrt m }} < < \frac{c}{{2\nu }}$ $ \Rightarrow $ les pics sont très étroits.
2.3°) Entre deux pics successifs $\Delta d = \frac{c}{{2\nu }} = \frac{\lambda }{2}$ (la moitié de la longueur d’onde).
2.4°) Si $\nu \to \nu + d\nu $, les abscisses des pics associés à $\nu $ sont ${d_q} = q\frac{c}{{2\nu }}$ et celles des pics associés à $\nu + d\nu $ sont $d{'_q} = q\frac{c}{{2(\nu + d\nu )}}$; on obtient une série de doubles pics.
2.5°) A la limite de séparation le bord droit, à mi-hauteur, d’un pic, coïncide avec le bord gauche, à mi-hauteur de l’autre pic.
La courbe ci-contre représente les deux pics dans cette position et la courbe résultante.
On aura séparation si $d{'_q} - {d_q} > 2\xi $ soit si $q\frac{c}{2}(\frac{1}{\nu } - \frac{1}{{\nu + d\nu }}) > 2\xi = \frac{2}{{\pi \nu \sqrt m }}$ $ \Rightarrow $ $\delta \nu > \frac{{2\nu }}{{q\pi \sqrt m }}$
Mais $d = \frac{{qc}}{{2\nu }}$ $ \Rightarrow $ $\delta \nu = \frac{c}{{d\pi \sqrt m }}$ ou $\delta {\nu _m} = \frac{{\varepsilon c}}{{2\pi d}}$
2.6°) $\varepsilon = {10^{ - 3}}\;et\;m = {4.10^6}$ $ \Rightarrow $ $\delta {\nu _m} = {10^6}Hz$
$d = q\frac{c}{{2\nu }}$ $ \Rightarrow $ $\Delta d = - d\frac{{\Delta \nu }}{\nu }$ or $\nu = \frac{c}{\lambda } = {4.74.10^{14}}Hz$
soit $\Delta d = - {10^{ - 10}}m$
on peut conclure avec certitude.
2.8°) ${I_{1\;\max }} = {I_0}$
2.9°) ${I_1} + {I_2} = {I_0}$
2.10°) $\frac{{{A_ - }}}{{{A_0}}} = \rho '\tau {e^{ - j\frac{\varphi }{2}}}\sum\limits_{q = 0}^\infty {\rho {'^{2q}}{e^{ - jq\varphi }}} $=$\frac{{\rho '\tau {e^{ - j\frac{\varphi }{2}}}}}{{1 - \rho {'^2}{e^{ - j\varphi }}}}$ $ \Rightarrow $ $\frac{{{I_ - }}}{{{I_0}}} = \frac{{1 - \varepsilon }}{\varepsilon }\frac{1}{{1 + m{{\sin }^2}\frac{\varphi }{2}}}$
$\frac{{{A_ - }}}{{{A_0}}} = \tau \sum\limits_{q = 0}^\infty {\rho {'^{2q}}{e^{ - jq\varphi }}} $=$\frac{\tau }{{1 - \rho {'^2}{e^{ - j\varphi }}}}$ $ \Rightarrow $ $\frac{{{I_ - }}}{{{I_0}}} = \frac{1}{\varepsilon }\;\frac{1}{{1 + m{{\sin }^2}\frac{\varphi }{2}}}$
$\varepsilon < < 1$ ${I_ - } \approx {I_ + } \approx \;\frac{1}{\varepsilon }\;\frac{1}{{1 + m{{\sin }^2}\frac{\varphi }{2}}}$ avec $m = \frac{4}{{{\varepsilon ^2}}}$; il y a résonance pour $I = {I_0}$.
2.11°) A travers une surface S parallèle aux miroirs, entre eux, le flux du vecteur de Poynting est $\vec \pi .\vec S = ({\vec \pi _ + } - {\vec \pi _ - }).\vec S$ et représente le différence entre le flux d’énergie dû à l’onde + et celui dû à l’onde -.
2.12°) Avec n entier relatif: $\varphi = 2\pi n + \frac{{4\pi d}}{c}(\nu - {\nu _n})$; à mi-hauteur $\sin 2\pi \frac{d}{c}(\nu - {\nu _n}) = \pm \frac{1}{{\sqrt m }}$ d’où $\delta \nu = \frac{c}{{d\pi \sqrt m }}$ et $\frac{{{I_1}}}{{{I_0}}} = \frac{1}{{1 + 4{{\left( {\frac{{\nu - {\nu _m}}}{{\Delta \nu }}} \right)}^2}}}$.
Le facteur 4 a été oublié dans le texte qui précisait bien largeur à mi-hauteur et non demi-largeur à mi-hauteur.
$Q = \frac{{{\nu _n}}}{{\Delta \nu }} = \frac{{d\pi \sqrt m \nu }}{c} = \frac{{2d\pi \nu }}{{\varepsilon c}} = \frac{{2d\pi }}{{\varepsilon \lambda }}$ $Q = {5.10^8}$
2.13°) On tient compte des durées de propagation; on étudie le régime transitoire du Fabry-Pérot; on prend la date t=0 quand le premier rayon transmis sort de l’appareil.
$\frac{{{A_1}}}{{{A_0}}} = {t^2}\sum\limits_{l = 0}^n {{r^{2l}}} {e^{ - jl\varphi }}$ avec $\varphi = 2q\pi $ (résonance) soit $\frac{{{A_1}}}{{{A_0}}} = {t^2}\sum\limits_{l = 0}^n {{r^{2l}}} $$ = 1 - {r^{2(n + 1)}}$ et $\frac{{{I_1}}}{{{I_0}}} = {\left[ {1 - {r^{2(n + 1)}}} \right]^2}$ avec $n = \frac{{ct}}{{2d}}$; ${I_1}$ tend vers zéro quand n tend vers l’infini; on se ramène à $\frac{{{I_1}}}{{{I_0}}} = {\left[ {1 - {r^{\frac{{ct}}{d}}}} \right]^2}$ après un décalage des temps légitime de 2d/c quand on passe d’une fonction discontinue en escalier à une fonction continue.
$\frac{{{A_1}}}{{{A_0}}} = {t^2}\sum\limits_{l = 0}^n {{r^{2l}}} {e^{ - jl\varphi }}$$ = {r^{2n + 1}}$ et $\frac{{{I_2}}}{{{I_0}}} = {r^{2(2n + 1)}}$; ${I_2}$ tend vers zéro quand n tend vers l’infini.
2.14°) ${r^2} = 1 - \varepsilon \approx {e^{ - \varepsilon }}$ $ \Rightarrow \;{I_1}(t) = {I_0}{\left( {1 - {e^{ - \frac{{\varepsilon ct}}{{2d}}}}} \right)^2}$; on ne trouve pas la formule du texte dans lequel l’exposant 2 a vraisemblablement été oublié.
2.15°) ${\tau _c} = \frac{{2d}}{{c\varepsilon }}$
2.17°) A l’instant initial, l’onde arrête d’émerger du Fabry-Pérot; la série géométrique est tronquée au début alors que c’était à la fin en 2.13°; $\frac{{{A_1}}}{{{A_0}}} = {\left( {\frac{{{A_1}}}{{{A_0}}}} \right)_{n \to \infty (2.13^\circ )}} - {\left( {\frac{{{A_1}}}{{{A_0}}}} \right)_{(2.13^\circ )}} = {r^{2(n + 1)}}$d’où $\frac{{{I_1}}}{{{I_0}}} = {r^{4(n + 1)}}$ et $\frac{{{I_1}}}{{{I_0}}} = {e^{ - \frac{{\varepsilon ct}}{d}}}$
et de même: $\frac{{{A_2}}}{{{A_0}}} = {\left( {\frac{{{A_2}}}{{{A_0}}}} \right)_{n \to \infty (2.13^\circ )}} - {\left( {\frac{{{A_2}}}{{{A_0}}}} \right)_{(2.13^\circ )}} = - {r^{2n + 1}}$d’où $\frac{{{I_2}}}{{{I_0}}} = {r^{2(2n + 1)}}$ et $\frac{{{I_2}}}{{{I_0}}} = {e^{ - \frac{{\varepsilon ct}}{d}}}$
2.18°) Pour les deux intensités, la limite, quand n tend vers l’infini, est nulle alors qu’en 2.13° elle est ${I_0}$ et 0 respectivement.
2.19°) L’onde n’est pas résonnante: si $n \to \infty $, pour l’établissement: $\frac{{{I_1}}}{{{I_0}}} \to \frac{1}{{1 + m{{\sin }^2}\frac{\varphi }{2}}}$ et $\frac{{{I_2}}}{{{I_0}}} \to \frac{{m{{\sin }^2}\frac{\varphi }{2}}}{{1 + m{{\sin }^2}\frac{\varphi }{2}}}$ alors que pour la rupture, les deux intensités tendent vers zéro.
2.20°) On indique « lentement » car il faut qu’un régime quasi-stationnaire soit réalisé et donc que la durée de déplacement soit très supérieure au temps de stockage de la cavité.
3.1°) On considère 2 miroirs identiques (pas dit dans le texte): $A\xrightarrow[{{M}_{1}}]{}{{A}_{1}}\xrightarrow[{{M}_{2}}]{}{{A}_{2}}\xrightarrow[{{M}_{1}}]{}{{A}_{3}}\xrightarrow[{{M}_{2}}]{}{{A}_{4}}$
${\overline {FA} _1}.\overline {FA} = {\overline {FA} _1}.{\overline {FA} _2}$ (formule de conjugaison de Newton) implique qu’après deux réflexions l’image A2 se confond avec l’objet A; le grandissement transversal, selon les formules de Newton, après ces deux réflexions est ${\gamma _t} = \frac{{ - {f_2}}}{{\overline {F{A_1}} }}.\frac{{ - \overline {F{A_1}} }}{{{f_1}}} = - 1$ et l’image d’un petit objet rectiligne perpendiculaire à l’axe est renversée; après 4 réflexions, deux sur chaque miroir, l’image d’un petit objet rectiligne perpendiculaire à l’axe se confond avec l’objet. D’après la relation de Lagrange-Helmoltz $G{\gamma _t} = - 1$ pour un miroir et +1 pour un nombre pair de miroirs; on a donc le grandissement angulaire G=1.
Après 4 réflexions le rayon repart du même point de l’axe dans les mêmes direction et sens.
3.2°) L = 2f = R (rayon des miroirs)
Soit A le point sur l’axe de révolution; tout rayon issu de A repasse en A après 4 réflexions, dans le cadre de l’approximation de Gauss, d’où: $(A{A_4}) = 4L = 8f = 4R$; le chemin optique ne dépend pas du rayon considéré (stigmatisme approché); il ne dépend pas de l’angle d’inclinaison; en posant $\varphi = \frac{{8\pi \nu R}}{c}$, on a le tableau suivant des amplitudes internes (juste avant sortie de la cavité):
| Faisceau 1 | Faisceau 2 | Faisceau 3 | Faisceau 4 | |
| Passage 1 | ${A_0}\tau {e^{ - j{\varphi _0}}}$ | ${A_0}\tau \rho '{e^{ - j{\varphi _1}}}$ | ${A_0}\tau \rho {'^2}{e^{ - j{\varphi _2}}}$ | ${A_0}\tau \rho {'^3}{e^{ - j\varphi }}$ |
| Passage 2 | ${A_0}\tau \rho {'^4}{e^{ - j{\varphi _0}}}{e^{ - j\varphi }}$ | ${A_0}\tau \rho {'^5}{e^{ - j{\varphi _1}}}{e^{ - j\varphi }}$ | ${A_0}\tau \rho {'^6}{e^{ - j{\varphi _2}}}{e^{ - j\varphi }}$ | ${A_0}\tau \rho {'^7}{e^{ - 2j\varphi }}$ |
| Passage 3 | ${A_0}\tau \rho {'^8}{e^{ - j{\varphi _0}}}{e^{ - 2j\varphi }}$ | ${A_0}\tau \rho {'^9}{e^{ - j{\varphi _1}}}{e^{ - 2j\varphi }}$ | ${A_0}\tau \rho {'^{10}}{e^{ - j{\varphi _2}}}{e^{ - 2j\varphi }}$ | ${A_0}\tau \rho {'^{11}}{e^{ - 3j\varphi }}$ |
$\frac{{{A_1}}}{{{A_0}}} = \tau \tau '{e^{ - j{\varphi _0}}}\sum\limits_{q = 0}^\infty \rho {'^{4q}}{e^{ - jq\varphi }} = \frac{{{t^2}{e^{ - j{\varphi _0}}}}}{{1 - {r^4}{e^{ - j\varphi }}}}$ $ \Rightarrow $ $\frac{{{I_1}}}{{{I_0}}} = \frac{{{{(1 - {r^2})}^2}}}{{{{(1 - {r^4})}^2} + 4{r^4}{{\sin }^2}\frac{\varphi }{2}}}$
$\frac{{{A_2}}}{{{A_0}}} = \tau \tau '\rho '{e^{ - j{\varphi _1}}}\sum\limits_{q = 0}^\infty \rho {'^{4q}}{e^{ - jq\varphi }} = \frac{{ - r{t^2}{e^{ - j{\varphi _1}}}}}{{1 - {r^4}{e^{ - j\varphi }}}}$ $ \Rightarrow $ $\frac{{{I_2}}}{{{I_0}}} = \frac{{{r^2}{{(1 - {r^2})}^2}}}{{{{(1 - {r^4})}^2} + 4{r^4}{{\sin }^2}\frac{\varphi }{2}}}$
$\frac{{{A_3}}}{{{A_0}}} = \tau \tau '\rho {'^2}{e^{ - j{\varphi _2}}}\sum\limits_{q = 0}^\infty \rho {'^{4q}}{e^{ - jq\varphi }} = \frac{{{r^2}{t^2}{e^{ - j{\varphi _2}}}}}{{1 - {r^4}{e^{ - j\varphi }}}}$ $ \Rightarrow $ $\frac{{{I_3}}}{{{I_0}}} = \frac{{{r^4}{{(1 - {r^2})}^2}}}{{{{(1 - {r^4})}^2} + 4{r^4}{{\sin }^2}\frac{\varphi }{2}}}$
$\frac{{{A_4}}}{{{A_0}}} = \rho + \tau \tau '\rho {'^3}{e^{ - j\varphi }}\sum\limits_{q = 0}^\infty \rho {'^{4q}}{e^{ - jq\varphi }} = \frac{{r(1 - {r^2}{e^{ - j\varphi }})}}{{1 - {r^4}{e^{ - j\varphi }}}}$ $ \Rightarrow $ $\frac{{{I_4}}}{{{I_0}}} = \frac{{{r^2}\left[ {{{(1 - {r^2})}^2} + 4{r^2}{{\sin }^2}\frac{\varphi }{2}} \right]}}{{{{(1 - {r^4})}^2} + 4{r^4}{{\sin }^2}\frac{\varphi }{2}}}$
On vérifie que la somme des quatre intensités est l’intensité incidente.
3.3°) Le trajet admet z’z comme axe de symétrie d’où ${\varphi _2} - {\varphi _0} = \frac{\varphi }{2}$ et $\frac{{{A_3}}}{{{A_1}}} = {r^2}{e^{ - j\frac{\varphi }{2}}}$; à la résonance $\varphi = 2q\pi $ $ \Rightarrow $
${A_1}\;et\;{A_3}$ sont en phase si q est pair et en opposition de phase si q est impair.
3.4°) Les rayons (1) et (3) sont confondus avec z’z; on se retrouve dans le cas d’un Fabry-Pérot plan-plan d’où $\frac{{{I_{13}}}}{{{I_0}}} = \frac{{{{(1 - {r^2})}^2}}}{{1 + {r^4} - 2{r^2}\cos \frac{\varphi }{2}}}$ ce qu’on retrouve mais par un calcul compliqué en faisant interférer les ondes (1) et (3).
Ceci revient à étudier la projection d’un rayon sur les plans xOz et yOz; il suffit d’étudier la marche d’un rayon méridien.
4.2°) On obtient quatre relations:
a) Dans le vide de gauche à droite: $y{'_n} = {y_n} + {\alpha _n}L$
b) Réflexion sur M2 , à droite: avec la relation de conjugaison (origine au sommet): $\alpha {'_n} = - {\alpha _n} - \frac{{2y{'_n}}}{{\overline {{S_2}{C_2}} }}$
c) Dans le vide de droite à gauche: ${y_{n + 1}} = {y_n} - \alpha {'_n}L$
d) Réflexion sur le miroir de gauche M1: ${\alpha _{n + 1}} = - \alpha {'_n} - \frac{{2{y_{n + 1}}}}{{\overline {{S_1}{C_1}} }}$
D’où par éliminations successives, la relation matricielle: $\left( {\begin{array}{*{20}{c}}{{y_{n + 1}}}\\{{\alpha _{n + 1}}}\end{array}} \right) = \left( {\begin{array}{*{20}{c}}{1 + \frac{{2L}}{{\overline {{S_2}{C_2}} }}}&{2L(1 + \frac{L}{{\overline {{S_2}{C_2}} }})}\\{\frac{2}{{\overline {{S_2}{C_2}} }} - \frac{2}{{\overline {{S_1}{C_1}} }} - \frac{{4L}}{{\overline {{S_1}{C_1}\;} \overline {{S_2}{C_2}} }}}&{1 + \frac{{2L}}{{\overline {{S_2}{C_2}} }} - \frac{{4L}}{{\overline {{S_1}{C_1}} }}(1 + \frac{L}{{\overline {{S_2}{C_2}} }})}\end{array}} \right)\left( {\begin{array}{*{20}{c}}{{y_n}}\\{{\alpha _n}}\end{array}} \right)$
On remarque que le déterminant de la matrice de transfert vaut l’unité; on peut le voir par calcul direct ou bien en calculant la matrice comme produit de quatre matrices élémentaires chacune de déterminant unité.
4.3°) $\left( {\begin{array}{*{20}{c}}{{y_n}}\\{{\alpha _n}}\end{array}} \right) = {M^n}\left( {\begin{array}{*{20}{c}}{{y_0}}\\{{\alpha _0}}\end{array}} \right)$; dans la base des vecteurs propres de M, M et sa puissance n sont diagonales d’éléments diagonaux les valeurs propres: $({\lambda _1},{\lambda _2})$ et $(\lambda _1^n,\lambda _2^n)$; on en déduit que la solution dans la base des vecteurs propres est ${Y_n} = \lambda _1^n{Y_0}$ et ${A_n} = \lambda _2^n{A_0}$; à l’aide de la matrice de changement de base, on repasse dans la base initiale; ${y_n}$ et ${\alpha _n}$ sont donc combinaisons linéaires de $\lambda _1^n\;et\;\lambda _2^n$; les coefficients ne dépendent pas de n; l’équation aux valeurs propres, avec le déterminant de la matrice de transfert égal à l’unité est: ${\lambda ^2} - \lambda trace(M) + 1 = 0$; on en déduit que le produit des valeurs propres (complexes) vaut l’unité: ${\lambda _1}{\lambda _2} = 1$; les valeurs propres peuvent s’écrire sous la forme: ${\lambda _1} = \rho {e^{i\theta }}$ et ${\lambda _2} = \frac{1}{\rho }{e^{ - i\theta }}$; si $\rho \ne 1$ l’une des racines a un module supérieur à l’unité et donc ${y_n}$ et ${\alpha _n}$ divergent quand n devient grand: il y a instabilité. Pour avoir stabilité, il faut $\rho = 1$.
4.4°) Les deux valeurs propres sont imaginaires: ${\lambda _1} = {e^{i\theta }}$ et ${\lambda _2} = {e^{ - i\theta }}$; de ce fait: $trace(M) = a + d = 2\cos \theta $; la condition de stabilité est donc: $ - 2 \le a + d \le 2$ soit en remplaçant a et d par leurs valeurs et en posant ${g_i} = 1 - \frac{L}{{{R_i}}}$ le résultat: $0 \le {g_1}{g_2} \le 1$.
4.5°) Le domaine de stabilité est compris entre les deux branches de l’hyperbole équilatère.
Pour le Fabry-Pérot plan-plan les rayons de courbures sont infinis: le point (1,1) est le point représentatif.
Pour le Fabry-Pérot confocal les rayons sont égaux à L, le point représentatif est l’origine des axes.
4.6°) On veut ${y_n} = {y_0}$, ${x_n} = {x_0}$, ${\alpha _n} = {\alpha _0}$, ${\beta _n} = {\beta _0}$ $ \Rightarrow {M^n} = I$ (matrice unité); dans la base des vecteurs propres, cette propriété reste vraie d’où $\lambda _1^n = 1\;et\;\lambda _2^n = 1$ et du fait que le produit des valeurs propres vaut l’unité: ${\lambda _1} = {e^{\frac{{2\pi iq}}{n}}}$ et ${\lambda _1} = {e^{ - \frac{{2\pi iq}}{n}}}$; d’où ${\lambda _1} + {\lambda _2} = 2\cos \frac{{2\pi q}}{n} = a + d$; avec les rayons égaux $\cos \frac{{2\pi q}}{n} = 1 - \frac{{4L}}{R} + 2\frac{{{L^2}}}{{{R^2}}}$ ce qui conduit à l’équation ${\left( {\frac{L}{R}} \right)^2} - 2\left( {\frac{L}{R}} \right) + {\sin ^2}\frac{{\pi q}}{n} = 0$ de racines $\frac{L}{R} = 1 \pm \cos \frac{{q\pi }}{n}$ $q \in \left\{ {0..n - 1} \right\}$.
4.7°) ${x_k}\;et\;{y_k}$ sont combinaisons linéaires de $\lambda _1^k\;et\;\lambda _2^k$ avec des coefficients indépendants de k; on en déduit ${x_k} = A\cos (2\pi \frac{{kq}}{n} + {\varphi _x})$ et ${y_k} = A\cos (2\pi \frac{{kq}}{n} + {\varphi _y})$; il suffit que $qk \in \left\{ {0..n - 1} \right\}$ pour avoir toutes les valeurs possibles; on a bien n taches qui se répartissent sur une ellipse définie par son équation paramétrique.
4.9°) Cavité multipassage: si n est élevé, le faisceau sera très affaibli (multiplication de l’intensité par ${r^{2n}}$); pour le Fabry-Pérot sphérique, à résonance, ${I_4} = \frac{{{I_0}}}{4}$; il est meilleur du point de vue de l’intensité émergente.
5.2°) Pour un métal parfait, en son voisinage: $\vec E = \frac{\sigma }{{{\varepsilon _0}}}\vec n$ et $\vec B = {\mu _0}{\vec j_s} \wedge \vec n$
5.3°) $div\vec E = 0 \Rightarrow \frac{{\partial f}}{{\partial y}} = 0$ soit $f = f(x,z)$
5.4°) $\frac{{{\partial ^2}f}}{{\partial {x^2}}} + \frac{{{\partial ^2}f}}{{\partial {z^2}}} + \frac{{{\omega ^2}}}{{{c^2}}}f = 0$
5.5°) Méthode de séparation des variables:$f(x,z)=h(x)k(z)\Rightarrow \frac{h''}{h}+\frac{k''}{k}+\frac{{{\omega }^{2}}}{{{c}^{2}}}=0$; pour pouvoir assurer les conditions limites, il faut: $\frac{h''}{h}=-{{\alpha }^{2}}$, $\frac{k''}{k}=-{{\gamma }^{2}}$ avec ${\alpha ^2} + {\gamma ^2} = \frac{{{\omega ^2}}}{{{c^2}}}$; les solutions sont sinusoïdales
et données par $h = A\cos \alpha x + B\sin \alpha x$ et $k = A\cos \gamma z + B\sin \gamma z$;
Pour $x = \pm \frac{X}{2}$ le champ électrique doit être normal $ \Rightarrow \vec E = 0$ et $h( \pm X/2) = 0$ $ \Rightarrow $ $A\cos \frac{{\alpha X}}{2} + B\sin \frac{{\alpha X}}{2} = A\cos \frac{{\alpha X}}{2} - B\sin \frac{{\alpha X}}{2} = 0$ et donc $\alpha = {n_1}\frac{\pi }{X}$ ${n_1} \in \aleph $
Pour $z = \pm \frac{Z}{2}$ le champ électrique doit être normal $ \Rightarrow \vec E = 0$ et $k( \pm Z/2) = 0$ $ \Rightarrow $
$C\cos \frac{{\gamma Z}}{2} + D\sin \frac{{\gamma Z}}{2} = C\cos \frac{{\gamma Z}}{2} - D\sin \frac{{\gamma Z}}{2} = 0$ et donc $\gamma = {n_2}\frac{\pi }{Z}$ ${n_2} \in \aleph $
Selon la parité de ces entiers: $f(x,z) = {E_0}\left( {\begin{array}{*{20}{c}}{\cos \alpha x}\\{ou}\\{\sin \alpha x}\end{array}} \right)x\left( {\begin{array}{*{20}{c}}{\cos \gamma z}\\{ou}\\{\sin \gamma z}\end{array}} \right)$; la solution du texte n’est valable que si les deux entiers sont impairs.
5.6°) $\alpha = {n_1}\frac{\pi }{X}$ $\gamma = {n_2}\frac{\pi }{Z}$
5.7°) $\frac{{{\omega ^2}}}{{{c^2}}} = \left( {\frac{{n_1^2}}{{{X^2}}} + \frac{{n_2^2}}{{{Z^2}}}} \right){\pi ^2}$ ${n_1}\;et\;{n_2} \in \aleph $
5.8°) On a une condition de résonance analogue à $d = q\frac{c}{{2\nu }}$
5.9°) $f(z) = {E_0}\cos \frac{{n\pi z}}{Z}$ si n est impair ou $f(z) = {E_0}\sin \frac{{n\pi z}}{Z}$ si n est pair; $\vec E = {E_0}\cos \frac{{n\pi z}}{Z}{\mathop{\rm Re}\nolimits} ({e^{i\omega t}}){\vec e_y}$ si n est impair.
5.10°) $\vec j = \sigma \vec E$; on fait l’hypothèse que la conductivité est réelle; l’équation de Maxwell-Ampère en régime sinusoïdal forcé s’écrit: $\vec \nabla \wedge \vec B = {\mu _0}(\sigma + i{\varepsilon _0}\omega )\vec E$ et donc $\vec \nabla \wedge \vec B \approx {\mu _0}\sigma \vec E$ si $\sigma > > {\varepsilon _0}\omega $; d’après l’équation de Maxwell-Faraday $\vec \nabla \wedge \vec E = - \frac{{\partial \vec B}}{{\partial t}}$ et la formule de calcul vectoriel $\vec \nabla \wedge (\vec \nabla \wedge \vec E) = \vec \nabla (\vec \nabla .\vec E) - \vec \Delta \vec E$, on obtient l’équation $\Delta \vec E = {\mu _0}\sigma \frac{{\partial \vec E}}{{\partial t}}$.
La solution générale est combinaison linéaire des deux solutions: $\vec{E}=\vec{E}{{'}_{0}}{{e}^{-\frac{1+i}{\delta }z}}{{e}^{i\omega t}}+\vec{E}{{''}_{0}}{{e}^{\frac{1+i}{\delta }z}}{{e}^{i\omega t}}$ soit
$\vec{E}=\vec{E}{{'}_{0}}{{e}^{-\frac{z}{\delta }}}{{e}^{i(\omega t-\frac{z}{\delta })}}+\vec{E}{{''}_{0}}{{e}^{+\frac{z}{\delta }}}{{e}^{i(\omega t+\frac{z}{\delta })}}$. Pour une propagation selon Oz: $\vec E = \vec E{'_0}{e^{ - \frac{z}{\delta }}}{e^{i(\omega t - \frac{z}{\delta })}}$; en plus le champ est transverse.
5.12°) Dans le métal:
$\vec \nabla \wedge \vec E = - i\omega \vec B$$ \Rightarrow $$\vec B = \frac{i}{\omega }\left( {\frac{{1 + i}}{\delta }} \right)({E_{0y}}{\vec e_x} - {E_{0x}}{\vec e_y}){e^{ - \frac{{1 + i}}{\delta }z}}{e^{i\omega t}}$ ou $\vec B = \frac{{i - 1}}{{\omega \delta }}(\vec E{'_0} \wedge {\vec e_z}){e^{ - \frac{{1 + i}}{\delta }z}}{e^{i\omega t}}$
Dans le vide:
$\vec E = {E_0}\cos \alpha z{e^{i\omega t}}{\vec e_y}$ et $\vec B = \frac{1}{{i\omega }}\frac{{\partial E}}{{\partial z}}{\vec e_x}$ $ \Rightarrow $ $\vec B = i\frac{{{E_0}\alpha }}{\omega }\sin \alpha z\;{e^{i\omega t}}{\vec e_x}$; or $\alpha = \frac{\omega }{c}$ est la norme du vecteur d’onde $ \Rightarrow $ $\vec B = i\frac{{{E_0}}}{c}\sin \alpha z\;{e^{i\omega t}}{\vec e_x}$
5.13°) En z=Z/2, on écrit:
la continuité du champ électrique selon y’y: $E{'_0}{e^{ - (1 + i)\frac{z}{{2\delta }}}} = {E_0}\cos \alpha \frac{Z}{2}$
la continuité du champ magnétique (pas de courants surfaciques) selon x’x: $\alpha {E_0}\sin \alpha \frac{Z}{2} = \frac{{(i - 1)}}{{\delta \omega }}E{'_0}{e^{ - \frac{{(1 + i)}}{{2\delta }}Z}}$
Pour avoir des champs non nuls, il faut que le déterminant du système soit nul: $\tan \alpha \frac{Z}{2} = \frac{{1 + i}}{{\delta \alpha }}$.
5.14°) Avec les expressions de $\delta $et de $\alpha $ on a $\tan \omega \frac{Z}{{2c}} = (1 + i)\sqrt {\frac{\sigma }{{2{\varepsilon _0}\omega }}} $ et ${\omega _0} = p\pi \frac{c}{Z} = (2q + 1)\pi \frac{c}{Z}$ (p est impair car le champ électrique est en cosinus); on a $\omega = {\omega _0} + \varepsilon $ $ \Rightarrow $ $\tan \left( {(q + \frac{1}{2})\pi + \varepsilon \frac{Z}{{2c}}} \right) = (1 + i){\left( {\frac{\sigma }{{2{\varepsilon _0}\omega }}} \right)^{\frac{1}{2}}}$
Au premier ordre près, on peut remplacer $\omega $ par ${\omega _0}$ et du fait que deux angles complémentaires ont des tangentes dont le produit vaut 1, on a: $ - \frac{1}{{\tan \frac{{\varepsilon Z}}{{2c}}}} \approx (1 + i)\sqrt {\frac{\sigma }{{2{\varepsilon _0}{\omega _0}}}} $; en assimilant la tangente à l’angle et en remplaçant ${\omega _0}$ par sa valeur, on obtient la formule du texte: $\omega = \frac{c}{Z}\left( {p\pi - \sqrt {\frac{{2{\varepsilon _0}{\omega _0}}}{\sigma }} + i\sqrt {\frac{{2{\varepsilon _0}{\omega _0}}}{\sigma }} } \right)$
5.15°) ${e^{i\omega t}} = {e^{i\frac{c}{Z}\left( {p\pi - \sqrt {\frac{{2{\varepsilon _0}{\omega _0}}}{\sigma }} } \right)t}}{e^{ - \sqrt {\frac{{2{\varepsilon _0}{\omega _0}}}{\sigma }} \frac{c}{Z}t}}$ $ \Rightarrow $ amortissement temporel de constante de temps $\tau = \frac{Z}{c}\sqrt {\frac{\sigma }{{2{\varepsilon _0}{\omega _0}}}} $; c’est comparable au régime transitoire du Fabry-Pérot quand on enlève la source (2.17°).
5.16°) $\vec \pi = \frac{{\vec E \wedge \vec B}}{{{\mu _0}}}$$ = \frac{{(\vec E + {{\vec E}^*}) \wedge (\vec B + {{\vec B}^*})}}{{4{\mu _0}}}$$ = \frac{{(\vec E \wedge \vec B + {{\vec E}^*} \wedge {{\vec B}^*} + {{\vec E}^*} \wedge \vec B + \vec E \wedge {{\vec B}^*})}}{{4{\mu _0}}}$$ \Rightarrow $
$\left\langle {\vec \pi } \right\rangle = $$\frac{{(\vec E \wedge {{\vec B}^*} + {{\vec E}^*} \wedge \vec B)}}{{4{\mu _0}}}$=$\frac{{{\mathop{\rm Re}\nolimits} ({{\vec E}^*} \wedge \vec B)}}{{2{\mu _0}}}$ ; or $\vec E(Z/2,t) = {E_0}\cos \alpha \frac{Z}{2}\;{e^{i\omega t}}{\vec e_y}$ et $\vec B(Z/2,t) = i\frac{{{E_0}}}{c}\sin \alpha \frac{Z}{2}\;{e^{i\omega t}}{\vec e_x}$ $ \Rightarrow $ $\left\langle {\vec \pi } \right\rangle = $-$\frac{{E_0^2}}{{2{\mu _0}c}}{\mathop{\rm Re}\nolimits} [i{(\cos \alpha \frac{Z}{2})^*}\sin \alpha \frac{Z}{2}]{\vec e_z}$ puis 5.13°$ \Rightarrow $$\left\langle {\vec \pi } \right\rangle = $-$\frac{{E_0^2}}{{2{\mu _0}c}}{\mathop{\rm Re}\nolimits} \left[ {\frac{{i(1 + i)}}{{\delta \alpha }}\;{{\left| {\cos \alpha \frac{Z}{2}} \right|}^2}} \right]{\vec e_z}$ = $\frac{{E_0^2}}{{2{\mu _0}}}\frac{{{{\left| {\cos \alpha \frac{Z}{2}} \right|}^2}}}{{\delta \omega }}\;{\vec e_z}$
On remplace $\alpha = \frac{\omega }{c}$ et $\omega $ par leurs valeurs ce qui donne:
$\left\langle {\vec \pi } \right\rangle = $ $\frac{{{\varepsilon _0}cE_0^2}}{2}\sqrt {\frac{\sigma }{{2{\varepsilon _0}{\omega _0}}}} \left( {c{h^2}\sqrt {\frac{{2{\varepsilon _0}{\omega _0}}}{\sigma }} - {{\sin }^2}\left( {(2n + 1)\frac{\pi }{2} - \sqrt {\frac{{2{\varepsilon _0}{\omega _0}}}{\sigma }} } \right)} \right){\vec e_z}$.
En remplaçant le carré du sinus par celui du cosinus de l’angle complémentaire et en effectuant un développement limité au premier ordre en $\frac{{{\varepsilon _0}{\omega _0}}}{{2\sigma }}$, on obtient: $\left\langle {\vec \pi } \right\rangle = \frac{{{\varepsilon _0}cE_0^2}}{4}\sqrt {\frac{{2{\varepsilon _0}{\omega _0}}}{\sigma }} {\vec e_z}$.
La densité moyenne d’énergie est $\left\langle w \right\rangle = \frac{{{\varepsilon _0}}}{4}\vec E.{\vec E^*} + \frac{{{\varepsilon _0}{c^2}}}{4}\vec B.{\vec B^*}$ et après calcul $\left\langle w \right\rangle = \frac{{{\varepsilon _0}E_0^2}}{4}ch2\sqrt {\frac{{2{\varepsilon _0}{\omega _0}}}{\sigma }} \frac{z}{Z}$; on peut alors calculer l’énergie dans la cavité par intégration sur son volume:
$W = \int\limits_{ - \frac{Z}{2}}^{\frac{Z}{2}} {wSdz} $$ = \frac{{{\varepsilon _0}E_0^2S}}{4}\frac{{sh\sqrt {\frac{{2{\varepsilon _0}{\omega _0}}}{\sigma }} }}{{\frac{1}{Z}\sqrt {\frac{{2{\varepsilon _0}{\omega _0}}}{\sigma }} }}$ et par développement limité au premier ordre: $W = \frac{{{\varepsilon _0}E_0^2}}{4}SZ$
La puissance perdue dans le métal est $P = 2\left\langle {\vec \pi .\vec S} \right\rangle $ $ = 2Wc\sqrt {\frac{{2{\varepsilon _0}{\omega _0}}}{\sigma }} $ en tenant compte des deux faces dans la cavité et par ailleurs $P = - \frac{{dW}}{{dt}}$; on obtient une équation différentielle linéaire du premier ordre à coefficients constants en W dont l’intégration donne $W = {W_0}{e^{ - \frac{t}{{\tau '}}}}$ avec $\tau ' = \sqrt {\frac{\sigma }{{2{\varepsilon _0}{\omega _0}}}} \frac{Z}{{2c}} = \frac{\tau }{2}$ ($\tau $ de 5.15°); quand on passe de l’amplitude à l’énergie, l’exposant est divisé par 2; l’énergie varie plus rapidement que l’amplitude.
Par ailleurs, le faisceau est étroit et donc limité latéralement; u varie rapidement avec x et y alors qu’il varie lentement en z. D’où: $\left| {\frac{{{\partial ^2}u}}{{\partial {z^2}}}} \right| < < \left| {\frac{{{\partial ^2}u}}{{\partial {x^2}}}} \right|\;et\;\left| {\frac{{{\partial ^2}u}}{{\partial {y^2}}}} \right|$ et $\left| {\frac{{\partial u}}{{\partial z}}} \right| < < \frac{{\left| u \right|}}{\lambda }$
6.2°) Le champ électrique vérifie: $\frac{{{\partial ^2}E}}{{\partial {x^2}}} + \frac{{{\partial ^2}E}}{{\partial {y^2}}} + \frac{{{\partial ^2}E}}{{\partial {z^2}}} + \frac{{{\omega ^2}}}{{{c^2}}}E = 0$; il suffit de le remplacer par $u(x,y,z){e^{i(\omega t - kz)}}$ avec $k = \frac{\omega }{c}$ pour obtenir $\frac{{{\partial ^2}u}}{{\partial {x^2}}} + \frac{{{\partial ^2}u}}{{\partial {y^2}}} + \frac{{{\partial ^2}u}}{{\partial {z^2}}} - 2ik\frac{{\partial u}}{{\partial z}} = 0$; or $k = \frac{{2\pi }}{\lambda }$; en tenant compte des approximations: $\frac{{{\partial ^2}u}}{{\partial {x^2}}} + \frac{{{\partial ^2}u}}{{\partial {y^2}}} - 2ik\frac{{\partial u}}{{\partial z}} = 0$ équation d’onde paraxiale.
6.3°) Pour une onde sphérique divergente en M(x,y,z), issue de O(0,0,0), en appelant r la distance à OM le champ est $E = \frac{{{E_0}}}{r}{e^{ - ikr}}{e^{i\omega t}}$ avec $r = \sqrt {{x^2} + {y^2} + {z^2}} $; en z>0 $E = \frac{{{E_0}}}{{\sqrt {{x^2} + {y^2} + {z^2}} }}{e^{ikz\left( {1 - \sqrt {1 + \frac{{{x^2} + {y^2}}}{{{z^2}}}} } \right)}}{e^{i(\omega t - kz)}}$ d’où ${u_S}(x,y,z) = \frac{{{E_0}}}{{\sqrt {{x^2} + {y^2} + {z^2}} }}{e^{ikz\left( {1 - \sqrt {1 + \frac{{{x^2} + {y^2}}}{{{z^2}}}} } \right)}}$. Pour une onde sphérique convergente en O, en z<0, on aurait la même expression.
6.4°) Si z >> x et y, alors $u{'_S}(x,y,z) = \frac{{{E_0}}}{z}{e^{ - ik\left( {\frac{{{x^2} + {y^2}}}{{2z}}} \right)}}$
6.5°) $\frac{{{\partial ^2}u{'_S}}}{{\partial {x^2}}} = - ik\frac{{{E_0}}}{{{z^2}}}{e^{ - ik\left( {\frac{{{x^2} + {y^2}}}{{2z}}} \right)}}\left( {1 - ik\frac{{{x^2}}}{z}} \right)$ et de même en y
d’où $\frac{{{\partial ^2}u{'_S}}}{{\partial {x^2}}} + \frac{{{\partial ^2}u{'_S}}}{{\partial {y^2}}} = - ik\frac{{{E_0}}}{{{z^2}}}{e^{ - ik\left( {\frac{{{x^2} + {y^2}}}{{2z}}} \right)}}\left( {2 - ik\frac{{{x^2} + {y^2}}}{z}} \right)$
Par ailleurs $2ik\frac{{\partial u{'_S}}}{{\partial z}} = ik\frac{{{E_0}}}{{{z^2}}}{e^{ - ik\left( {\frac{{{x^2} + {y^2}}}{{2z}}} \right)}}\left( {2 - ik\frac{{{x^2} + {y^2}}}{z}} \right)$; on en déduit: $\frac{{{\partial ^2}u{'_S}}}{{\partial {x^2}}} + \frac{{{\partial ^2}u{'_S}}}{{\partial {y^2}}} - 2ik\frac{{\partial u{'_S}}}{{\partial z}} = 0$
$u{'_S}$ est solution exacte de l’équation d’onde paraxiale.
6.6°) $u(x,y,z) = A(z){e^{ - ik\left( {\frac{{{x^2} + {y^2}}}{{2q(z)}}} \right)}}$; le même genre de calcul qu’en 6.5° donne: $\frac{{2ik}}{A}\frac{{dA}}{{dz}} + \left( {\frac{{{k^2}}}{{{q^2}}}({x^2} + {y^2})(1 - \frac{{dq}}{{dz}}) + \frac{{2ik}}{q}} \right) = 0$; on cherche A=A(z) et de ce fait le coefficient de ${x^2} + {y^2}$ doit être nul $ \Rightarrow $ $\frac{{dq}}{{dz}} = 1$ et $q(z) = {q_0} + z - {z_0}$; puis $\frac{{dA}}{{dz}} = - \frac{A}{{q(z)}}$ soit en intégrant $A(z)q(z) = cste$ ou $A(z) = {A_0}\frac{{{q_0}}}{{q(z)}}$
6.7°) $u(x,y,z) = \frac{{{A_0}{q_0}}}{{{q_0} + z - {z_0}}}{e^{ - ik\left( {\frac{{{x^2} + {y^2}}}{{2(q + z - {z_0})}}} \right)}}$ et selon le texte $u(x,y,z) = {u_0}B{e^{ - ikB\left( {\frac{{{x^2} + {y^2}}}{2}} \right)}}$ avec $B = \frac{1}{{R(z)}} - \frac{{2i}}{{k{w^2}(z)}}$; en identifiant les phases on en déduit $B = \frac{1}{{R(z)}} - \frac{{2i}}{{k{w^2}(z)}} = \frac{1}{{q(z)}} = \frac{1}{{{q_0} + z - {z_0}}}$ et en identifiant les amplitudes ${u_0} = {A_0}{q_0}$.
d’où $R(z) = \frac{{q_2^2}}{{{q_1} + z - {z_0}}} + {q_1} + z - {z_0}$ et ${w^2}(z) = \frac{{2{q_2}}}{k}\left( {1 + \frac{{{{({q_1} + z - {z_0})}^2}}}{{q_2^2}}} \right)$
R(z) représente le rayon de courbure de l’onde; il varie avec z; l’onde est plane si R devient infini et donc si ${q_1} = 0$ et $z = {z_0}$; on pose ${w_0} = w({z_0})$ et on obtient ${q_2} = \frac{{kw_0^2}}{2} = {Z_0}$ (longueur de Rayleigh); avec ces notations: ${Z_0} = {q_2} = \frac{{\pi w_0^2}}{\lambda }$ et ${q_0} = i{Z_0}$ puis $R(z) = \frac{{Z_0^2}}{{z - {z_0}}} + z - {z_0}$ et $w(z) = {w_0}{\left( {1 + {{\left( {\frac{{z - {z_0}}}{{{Z_0}}}} \right)}^2}} \right)^{\frac{1}{2}}}$
6.9°) En remplaçant dans l’expression du champ électrique, on trouve: $E = {A_0}\frac{{{e^{ - iArc\tan \left( {\frac{{z - {z_0}}}{{{Z_0}}}} \right)}}}}{{{{\left[ {1 + {{\left( {\frac{{z - {z_0}}}{{{Z_0}}}} \right)}^2}} \right]}^{\frac{1}{2}}}}}{e^{ - \frac{{ik{r^2}}}{{2\left( {z - {z_0} + \frac{{Z_0^2}}{{z - {z_0}}}} \right)}}}}{e^{ - \frac{{k{r^2}}}{{2\left[ {1 + {{\left( {\frac{{z - {z_0}}}{{{Z_0}}}} \right)}^2}} \right]{Z_0}}}}}{e^{i(\omega t - kz)}}$ avec $r = \sqrt {{x^2} + {y^2}} $
Pour une surface d’onde, la phase est constante d’où: $kz + Arc\tan \left( {\frac{{z - {z_0}}}{{{Z_0}}}} \right) + \frac{{k{r^2}}}{{2\left( {z - {z_0} + \frac{{Z_0^2}}{{z - {z_0}}}} \right)}} = cste$
w(z) est la distance, selon une direction perpendiculaire à l’axe du faisceau, au bout de laquelle l’amplitude est divisée par e et l’intensité par e2; on l’appelle le rayon focal: il est fonction de z.
6.10°) $w\frac{{dw}}{{dz}} = w_0^2\frac{{z - {z_0}}}{{{Z_0}}}$ s’annule si $z = {z_0}$; on a un minimum de w(z); en cet endroit le faisceau a une « section » minimale de rayon focal ${w_0}$(« waist » en anglais) et le rayon de courbure est infini. Le texte parle de « foyer », mais le nom est incorrect.
L’approximation $\left| {\frac{{\partial u}}{{\partial z}}} \right| < < \frac{{\left| u \right|}}{\lambda }$ est vérifiée si $r < < \frac{{kw_0^2}}{2}$.
Enfin d’après l’expression du champ de 6.9°, l’abscisse z0 de la zone à rayon focal minimal et la valeur w0 de ce minimum déterminent totalement la géométrie du faisceau.
6.11°) L’onde en sortie est sphérique convergente de centre le foyer image F.
6.12°) On note e l’épaisseur de la lentille mince et n l’indice du verre dont elle est faite. Dans le cadre de l’approximation de Gauss, un rayon incident parallèle à l’axe traverse la lentille mince selon le segment IJ très court (inférieur à e) par rapport aux rayons de courbure R1 et R2 des faces et peu incliné par rapport à l’axe de la lentille. Le retard de phase introduit par la présence de la lentille est donc $\phi (r) = k(n - 1)IJ$. Soit en appelant H et H’ les projections de I et J sur l’axe et S1 et S2 les sommets des faces: $\phi (r) = k(n - 1)(e - \overline {{S_1}H} - \overline {H'{S_2}} )$; pour évaluer les deux segments, on raisonne sur le cercle ci-contre.
Soit α l’angle entre SS’ et IS’ qu’on retrouve entre IS et IH: $\tan \alpha = \frac{r}{{2R - \overline {SH} }} = \frac{{\overline {SH} }}{r}$ $ \Rightarrow $ $\overline {SH} \approx \frac{{{r^2}}}{{2R}}$ $ \Rightarrow $
$\phi (r) = k(n - 1)\left( {e - \frac{{{r^2}}}{2}\left( {\frac{1}{{{R_1}}} + \frac{1}{{{R_2}}}} \right)} \right)$ ; or la vergence de la lentille est $V = \frac{1}{{f'}} = (n - 1)\left( {\frac{1}{{{R_1}}} + \frac{1}{{{R_2}}}} \right)$ d’où $\phi (r) = \phi (0) - k\frac{{{V^2}}}{2}{r^2}$
Les rayons de courbure sont comptés avec la convention: ${R_1} = \overline {{S_1}{C_1}} $ et ${R_2} = - \overline {{S_2}{C_2}} $(attention au signe moins)
6.13°) Soit un point A sur z’z émettant une onde sphérique divergente avec $\overline {OA} = {z_1}$.
$E = \frac{{{E_0}}}{{\left| {z - {z_1}} \right|}}{e^{ - ik\frac{{{r^2}}}{{2(z - {z_1})}}}}{e^{i(\omega t - kz)}}$ pour $z > {z_1}$; en z=0 et après traversée de la lentille, $E = \frac{{{E_0}}}{{\left| {{z_1}} \right|}}{e^{ - ik\frac{{{r^2}}}{{2{z_1}}}}}{e^{ - i(\phi (r) - \phi (0))}}{e^{i(\omega t - \phi (0))}}$$ = \frac{{{E_0}}}{{\left| {{z_1}} \right|}}{e^{ik\frac{{{r^2}}}{{2{z_1}}}\left( {\frac{1}{{{z_1}}} + \frac{1}{{f'}}} \right)}}{e^{i(\omega t - \phi (0))}}$expression compatible avec une onde sphérique divergente centrée en A’, d’abscisse z2 positive qui s’écrit: $E = \frac{{\underline {E{'_0}} }}{{\left| {{z_2}} \right|}}{e^{ik\frac{{{r^2}}}{{2{z_2}}}}}{e^{i\omega t}}$; on ne cherche pas la relation entre les amplitudes complexes; il suffit d’identifier les phases et ce pour toute valeur de r dans le cadre de l’approximation de Gauss. On en déduit: $\frac{1}{{{z_2}}} - \frac{1}{{{z_1}}} = \frac{1}{{f'}} = V$; on peut généraliser à un système centré mince quelconque (indices extrêmes n et n’); il introduit un retard de phase $\phi (r) = \phi (0) - {k_0}\frac{{{V^2}}}{2}{r^2}$ ce qui conduit à $\frac{{f'}}{{{z_2}}} + \frac{f}{{{z_1}}} = 1$ avec $V = \frac{{n'}}{{f'}} = - \frac{n}{f}$; pour un dioptre sphérique: $V = \frac{{n' - n}}{{\overline {SC} }}$ et pour un miroir sphérique $V = \frac{{ - 2n}}{{\overline {SC} }}$.
6.14°) Pour l’onde incidente en z=0, ${E_1}(x,y,0,t) = {u_{01}}\left( {\frac{1}{{{R_1}(0)}} - \frac{{2i}}{{kw_1^2(0)}}} \right){e^{ - \frac{{ik{r^2}}}{{2{R_1}(0)}}}}{e^{ - \frac{{{r^2}}}{{w_1^2(0)}}}}{e^{i\omega t}}$
Juste après traversée de la lentille: ${E_2}(x,y,0,t) = {u_{01}}\left( {\frac{1}{{{R_1}(0)}} - \frac{{2i}}{{kw_1^2(0)}}} \right){e^{ - \frac{{ik{r^2}}}{{2{R_1}(0)}}}}{e^{\frac{{ikV{r^2}}}{2}}}{e^{ - \frac{{{r^2}}}{{w_1^2(0)}}}}{e^{i\omega t}}$ ce qui est compatible avec une onde émergente du même type: ${E_2}(x,y,0,t) = {u_{02}}\left( {\frac{1}{{{R_2}(0)}} - \frac{{2i}}{{kw_2^2(0)}}} \right){e^{ - \frac{{ik{r^2}}}{{2{R_2}(0)}}}}{e^{ - \frac{{{r^2}}}{{w_1^2(0)}}}}{e^{i\omega t}}$
En identifiant les exposants imaginaires en r2, on a: $\frac{1}{{{R_1}(0)}} - \frac{1}{{{R_2}(0)}} = V$ et ${w_1}(0) = {w_2}(0)$; la première relation est la relation de conjugaison des « foyers » et la seconde exprime la continuité du rayon focal sur la lentille.
On a $\frac{1}{{{q_1}(0)}} - \frac{1}{{{q_2}(0)}} = V$; ${R_2}(0) = - \left( {\frac{{Z_2^2}}{{{z_2}}} + {z_2}} \right)$ et ${R_1}(0) = - \left( {\frac{{Z_1^2}}{{{z_1}}} + {z_1}} \right)$; ${Z_1} = \frac{{kw_1^2}}{2}$ et ${Z_2} = \frac{{kw_2^2}}{2}$;
${w_1}(0) = {w_1}{\left( {1 + {{\left( {\frac{{{z_1}}}{{{Z_1}}}} \right)}^2}} \right)^{\frac{1}{2}}}$et ${w_2}(0) = {w_2}{\left( {1 + {{\left( {\frac{{{z_2}}}{{{Z_2}}}} \right)}^2}} \right)^{\frac{1}{2}}}$
On obtient: $w_2^2\left( {1 + {{\left( {\frac{{{z_2}}}{{{Z_2}}}} \right)}^2}} \right) = w_1^2\left( {1 + {{\left( {\frac{{{z_1}}}{{{Z_1}}}} \right)}^2}} \right)$ et $\frac{1}{{{z_2} + \frac{{Z_2^2}}{{{z_2}}}}} - \frac{1}{{{z_1} + \frac{{Z_1^2}}{{{z_1}}}}} = V = \frac{1}{{f'}}$
Comme en 6.13° pour un système mince $\frac{{f'}}{{{q_2}(0)}} + \frac{f}{{{q_1}(0)}} = 1$.
A partir des 2 équations à 2 inconnues obtenues on peut calculer w2 et z2:
$w_2^2 = \frac{{w_1^2\left( {1 + {{\left( {\frac{{{z_1}}}{{{Z_1}}}} \right)}^2}} \right)}}{{1 + {{\left[ {V\left( {{Z_1} + \frac{{z_1^2}}{{{Z_1}}}} \right) + \frac{{{z_1}}}{{{Z_1}}}} \right]}^2}}}$ et ${z_2} = \frac{{\left[ {1 + {{\left( {\frac{{{z_1}}}{{{Z_1}}}} \right)}^2}} \right]\left( {{z_1} + V(Z_1^2 + z_1^2)} \right)}}{{1 + {{\left[ {V\left( {{Z_1} + \frac{{z_1^2}}{{{Z_1}}}} \right) + \frac{{{z_1}}}{{{Z_1}}}} \right]}^2}}}$
Mais ces expressions ne servent à rien ensuite; merci d’en avoir demandé le calcul!
et $w_2^2\left( {1 + {{\left( {\frac{{{z_2}}}{{{Z_2}}}} \right)}^2}} \right) = w_1^2\left( {1 + {{\left( {\frac{{{z_1}}}{{{Z_1}}}} \right)}^2}} \right)$ et $\frac{1}{{{z_2} + \frac{{Z_2^2}}{{{z_2}}}}} + \frac{1}{{{z_1} + \frac{{Z_1^2}}{{{z_1}}}}} = V = \frac{1}{{f'}}$
Le faisceau est stable si la zone de resserrement est unique (le faisceau résultant a une forme gaussienne) caractérisé par w1 et $Z = \frac{{kw_1^2}}{2}$ et par les distances algébriques z1, z2 aux miroirs avec $L = {z_2} - {z_1}$; à partir de la relation de conjugaison, on obtient: ${z_1} + \frac{{{Z^2}}}{{{z_1}}} = - {R_1}$ et ${z_2} + \frac{{{Z^2}}}{{{z_2}}} = {R_2}$; on remarque que les rayons de courbure du faisceau gaussien au niveau des miroirs sont les rayons de courbure des miroirs.
On a 3 équations à trois inconnues qui permettent de déterminer z1, z2 et w1. On calcule seulement z1, z2.
${z_2} = \frac{{L({R_1} - L)}}{{{R_1} + {R_2} - 2L}}$ ${z_1} = \frac{{L(L - {R_2})}}{{{R_1} + {R_2} - 2L}}$ ${Z^2} = \frac{{L({R_1} - L)({R_2} - L)({R_1} + {R_2} - L)}}{{{{({R_1} + {R_2} - 2L)}^2}}}$
Avec ${g_i} = 1 - \frac{L}{{{R_i}}}$ on peut écrire ${Z^2} = {L^2}\frac{{{g_1}{g_2}(1 - {g_1}{g_2})}}{{{{({g_1} + {g_2} - 2{g_1}{g_2})}^2}}}$>0 $ \Rightarrow $ $0 < {g_1}{g_2} < 1$; c’est la condition de stabilité.
Notons que ${z_1} = - L\frac{{{g_2}(1 - {g_1})}}{{{g_1} + {g_2} - 2{g_1}{g_2}}}$ et ${z_2} = L\frac{{{g_1}(1 - {g_2})}}{{{g_1} + {g_2} - 2{g_1}{g_2}}}$
6.16°) Si les deux rayons de courbure sont égaux: ${Z^2} = \frac{L}{4}(2R - L) = \left( {\frac{{kw_1^2}}{2}} \right)$ $ \Rightarrow $ $w_1^2 = \frac{1}{k}\sqrt {(2R - L)L} $
La condition de stabilité est réalisée si R > L/2.
6.17°) Condition de résonance: sur un aller et retour, le long de z’z en particulier, le déphasage doit être un multiple entier de fois $2\pi $ soit sur un aller seulement un multiple entier de fois $\pi $; or $\varphi (z) = kz - Arc\tan \frac{{{z_0}}}{{{Z_0}}}$ et donc ${\varphi _2} - {\varphi _1} = k({z_2} - {z_1}) - (Arc\tan \frac{{{z_2}}}{Z} - Arc\tan \frac{{{z_1}}}{Z}) = q\pi $, q entier positif ou nul; on pose $\gamma = Arc\tan \frac{{{z_2}}}{Z} - Arc\tan \frac{{{z_1}}}{Z}$; le calcul donne ${\cos ^2}\gamma = {g_1}{g_2}$ puis $\nu = \frac{c}{{2L}}\left( {q + \frac{1}{\pi }Arc\cos \sqrt {{g_1}{g_2}} } \right)$; si les deux rayons sont égaux $\nu = \frac{c}{{2L}}\left( {q + \frac{1}{\pi }Arc\cos \left( {1 - \frac{L}{R}} \right)} \right)$.
7.1°) L’équation de propagation de la composante x du champ électrique est $\frac{{{\partial ^2}{E_x}}}{{\partial {x^2}}} + \frac{{{\partial ^2}{E_x}}}{{\partial {y^2}}} + \frac{{{\partial ^2}{E_x}}}{{\partial {z^2}}} + \frac{{{\omega ^2}}}{{{c^2}}}{E_x} = 0$
${{E}_{x}}=f(x)g(y)h(z)\Rightarrow \frac{f''}{f}+\frac{g''}{g}+\frac{h''}{h}+\frac{{{\omega }^{2}}}{{{c}^{2}}}=0$; pour pouvoir assurer les conditions limites, il faut: $\frac{f''}{f}=-k_{x}^{2}$ $\frac{g''}{g}=-k_{y}^{2}$ et $\frac{h''}{h}=-k_{z}^{2}$ avec $k_x^2 + k_y^2 + k_z^2 = \frac{{{\omega ^2}}}{{{c^2}}}$; avec un des sommets de la cavité à l’origine des axes:
$f(x) = A\cos {k_x}x + B\sin {k_x}x$, $g(y) = C\cos {k_y}y + D\sin {k_y}y$, $h(z) = E\cos {k_z}z + F\sin {k_z}z$
Les conditions limites sont:
${E_x}(x = 0\;et\;x = X) = {E_y}(x = 0\;et\;x = X) = 0$
${E_z}(y = 0\;et\;y = Y) = {E_x}(y = 0\;et\;y = Y) = 0$
${E_x}(z = 0\;et\;z = Z) = {E_y}(z = 0\;et\;z = Z) = 0$
g(0) = g(Y) = 0 et h(0) = h(Z) impliquent C = E = 0
$g(y) = D\sin {k_y}y$ $h(z) = F\sin {k_z}z$
${k_y} = \pm \frac{{m\pi }}{Y}$ ${k_z} = \pm \frac{{n\pi }}{Z}$
${E_x} = ({A_1}\cos {k_x}x + {B_1}\sin {k_x}x)\sin {k_y}y\sin {k_z}z{e^{i\omega t}}$ et de même ${E_y} = \sin k{'_x}x({A_2}\cos k{'_y}y + {B_2}\sin k{'_y}y)\sin k{'_z}z{e^{i\omega t}}$
${{E}_{z}}=\sin k{{''}_{x}}x\sin k{{''}_{y}}y({{A}_{3}}\cos k{{''}_{z}}z+{{B}_{3}}\sin k{{''}_{z}}z){{e}^{i\omega t}}$
Du fait que $div\vec E = 0$, il existe une combinaison linéaire entre les dérivées de ces composantes vraie pour tout x,y,z dans le domaine de la cavité; on peut en conclure qu’on a les mêmes composantes de vecteur d’onde entre les trois composantes du champ et donc que ${k_x} = \pm \frac{{l\pi }}{X}$ ${k_y} = \pm \frac{{m\pi }}{Y}$ ${k_z} = \pm \frac{{n\pi }}{Z}$ avec l,m,n $ \in \aleph $.
La combinaison linéaire est également vraie en x = 0 ou X, en y = 0 ou Y, en z = 0 ou Z; on en déduit ${B_1} = {B_2} = {B_3} = 0$ et ${A_1}l + {A_2}m + {A_3}n = 0$; en fait, il n’existe que deux constantes indépendantes;
${E_x} = {A_1}\cos {k_x}x\sin {k_y}y\sin {k_z}z{e^{i\omega t}}$ ${E_y} = {A_2}\sin {k_x}x\cos {k_y}y\sin {k_z}z{e^{i\omega t}}$ ${E_z} = {A_3}\sin {k_x}x\sin {k_y}y\cos {k_z}z{e^{i\omega t}}$
On peut également calculer les composantes du champ magnétique et vérifier que le champ magnétique a des composantes normales nulles sur les faces de la cavité.
Enfin $k_x^2 + k_y^2 + k_z^2 = \frac{{{\omega ^2}}}{{{c^2}}}$ implique $\nu = \frac{c}{2}{\left( {\frac{{{l^2}}}{{{X^2}}} + \frac{{{m^2}}}{{{Y^2}}} + \frac{{{n^2}}}{{{Z^2}}}} \right)^{\frac{1}{2}}}$.
7.3°) Le calcul de I fait intervenir des intégrales du type $\int\limits_0^X {\cos {n_1}\frac{\pi }{X}\cos {n_2}\frac{\pi }{X}dx} $ ou bien en sinus, qu’on linéarise en intégrales de cosinus faisant figurer la somme ou la différence des deux entiers; ces intégrales sont nulles si les entiers sont différents. De ce fait $I = 0$.
7.4°) Les champs électrique et magnétique sont combinaison linéaire des champs des modes propres; quand on les remplace dans l’expression de la densité d’énergie électromagnétique on fait intervenir en développant des intégrales de produits de champs qui sont nulles et des intégrales proportionnelles au carré des champs des modes propres; pour chaque mode un terme est proportionnel au carré du champ électrique et un autre au carré du champ magnétique; on a deux termes quadratiques par mode propre; en retenant, selon le théorème d’équipartition de l’énergie, l’énergie kT/2 par degré de liberté, on a l’énergie kT par mode propre.
On retrouve le théorème de Rayleigh-Jeans qui dit que chaque mode est équivalent à un oscillateur harmonique linéaire. D’où:
$dU(\nu ) = {\rm N}(\nu )d\nu = V\frac{{8\pi {\nu ^2}kT}}{{{c^3}}}d\nu $ soit une densité d’énergie spectrale $u(\nu ) = \frac{{8\pi {\nu ^2}kT}}{{{c^3}}}$.
7.5°) ${U_t} = \int\limits_0^\infty {U(\nu )d\nu } = \frac{{\pi kTV}}{{{c^3}}}\int\limits_0^\infty {{\nu ^2}d\nu } $ ; l’intégrale n’est pas définie; l’énergie emmagasinée ne peut être infinie.
7.6°) La probabilité de l’énergie ${E_n} = nh\nu $ pour le mode propre de fréquence $\nu $ est ${P_n} = A{e^{ - \frac{{nh\nu }}{{kT}}}}$; or $\sum\limits_{n = o}^\infty {{P_n}} = 1$(ne pas oublier n=0; la probabilité de l’état d’énergie nulle est non nulle); d’où ${P_n} = \frac{{{e^{ - \frac{{nh\nu }}{{kT}}}}}}{{\sum\limits_{n = 0}^\infty {{e^{ - \frac{{nh\nu }}{{kT}}}}} }}$
7.7°) L’énergie moyenne du mode de fréquence $\nu $ est ${\rm E}(\nu ) = \sum\limits_{n = o}^\infty {{P_n}} {E_n}$ $ = \frac{{\sum\limits_{n = 0}^\infty {nh\nu {e^{ - \frac{{nh\nu }}{{kT}}}}} }}{{\sum\limits_{n = 0}^\infty {{e^{ - \frac{{nh\nu }}{{kT}}}}} }}$
$x = \frac{{h\nu }}{{kT}}$ $ \Rightarrow $${\rm E}(\nu ) = xkT\frac{{\sum\limits_{n = 0}^\infty {n{e^{ - nx}}} }}{{\sum\limits_{n = 0}^\infty {{e^{ - nx}}} }}$$ = - xkT\frac{{\frac{d}{{dx}}\sum\limits_{n = 0}^\infty {n{e^{ - nx}}} }}{{\sum\limits_{n = 0}^\infty {{e^{ - nx}}} }}$$ = - xkT\frac{d}{{dx}}\ln \sum\limits_{n = 0}^\infty {{e^{ - nx}}} $$ = - xkT\frac{d}{{dx}}\ln \frac{1}{{1 - {e^{ - x}}}}$$ = kT\frac{x}{{{e^x} - 1}}$
${\rm E}(\nu ) = \frac{{h\nu }}{{{e^{\frac{{h\nu }}{{kT}}}} - 1}}$.
En fait cette démonstration n’est pas valable car les photons obéissent à la statistique de Bose-Einstein et l’énergie d’un oscillateur linéaire n’est pas ${E_n} = nh\nu $ mais ${E_n} = (n + \frac{1}{2})h\nu $; dans l’état fondamental, à une température absolue de O K, avec la formule du texte, l’oscillateur à une énergie nulle; c’est-à-dire que la somme de l’énergie cinétique $\frac{1}{2}m{v^2}$ et de l’énergie potentielle $\frac{1}{2}k{x^2}$est nulle; de ce fait vitesse et abscisse sont nulles simultanément ce qui est contraire au principe d’indétermination de Heisenberg.
7.9°) On peut définir la densité d’énergie totale ${u_t} = \frac{1}{V}\int\limits_0^\infty {U(\nu )d\nu } $, d’une part car l’intégrale qui l’exprime est définie mathématiquement et d’autre part car on a équilibre thermique; l’énergie se répartit sur tous les modes et se répartit également dans l’espace de la cavité.
7.10°) $x = \frac{{h\nu }}{{kT}}$ ${u_t} = \frac{{8\pi h}}{{{c^3}}}{\left( {\frac{{kT}}{h}} \right)^4}\int\limits_0^\infty {\frac{{{x^3}dx}}{{{e^x} - 1}}} $ soit ${u_t} = \sigma {T^4}$
avec $\sigma = \frac{{8{\pi ^5}{k^4}}}{{15{h^3}{c^3}}}$ ; c’est la loi de Stéphan-Boltzmann; la densité d’énergie totale est proportionnelle à la puissance quatrième de la température absolue.